Problem
This tip demonstrates how to use SQL RAND function to simulate a simplified version of casino craps, a well-known dice game played in gambling casinos. This type of simulation falls under the broader category of Monte Carlo simulations, named after the famed Monte Carlo Casino in Monaco. Monte Carlo simulations are widely used across various fields, including insurance risk assessment, disease spread modeling, weather forecasting, and computerized game design, such as state lotteries. These applications all rely on sampling from a function that generates a random sequence of values, enabling realistic probabilistic modeling.
Solution
I was introduced to Monte Carlo simulations in graduate school decades ago. Over the following years, I remained intrigued by Monte Carlo simulations because of their ability to model relatively complex processes with simple computer programs that call a pseudo-random number generator, such as SQL Server’s RAND() function. The SQL RAND function returns values from a distribution with a uniform or flat shape. Some other data distributions commonly used in Monte Carlo simulations include the normal, log-normal, and Weibull distributions. The exponential and Poisson distributions are another pair of distributions that are widely referenced when simulating processes with wait times (Predict Wait Times and Simulating Wait Times), such as modeling patient wait times with different emergency severities, staff availability, and peak hours. Monte Carlo methods help account for randomness, giving probability distributions instead of a single point estimate.
Aside from a distribution of random values, Monte Carlo simulations require a set of rules for generating outcomes. The combination of the underlying random value distribution and the rules for converting random numbers to simulation outcomes determines the behavior of the simulation in a set of single rounds. By running a Monte Carlo simulation many times, analysts can gain an understanding of the distribution of final outcomes projected by a Monte Carlo simulation model as well as the path to final outcomes. To the extent that the random values reflect the variation in a process and the rules for converting random values into simulation outcomes correspond to the behavior of a process, the Monte Carlo simulation outcomes will reflect those in the process being modeled.
This tip applies the rules for two common craps bets – namely, “pass line” versus “don’t pass line” bets. Several rules associated with each bet define how a player can win or lose. The main reason this tip calls the game “simplified” is because there are numerous other kinds of bets that can be placed in a craps game at a casino. The simplified version modeled in this tip is meant to help readers grasp the interplay between random function return values and game rules.
Selected other Monte Carlo use cases are listed in this tip’s Problem section. No matter what use case you are modeling with a Monte Carlo simulation, the approach always depends on an underlying random number function and rules for converting the random function return values to outcomes from successive simulation runs.
Elements of a Simplified Casino Craps Simulation
There are three elements for the simplified casino craps simulation implemented in this tip. Each type of element is stored in a SQL Server table. These tables are for the players, the dice_rolls, and the bets in the simplified casino craps simulation.
- The players table has three columns – one for the player identifier, another for the player name, and a final one for the bankroll from which a player can extract funds to place bets. There is a separate row in the players table for each player in a simulation round. Within a craps game, one of the players must shoot the dice one or more times for each simulation round. The simulation populates the @shooter_id local variable to designate the shooter for a simulation round. The @shooter_id local variable value must match one of the player_id column values from the players table.
- The bets table has five columns and a separate row for each bet placed by players in the current simulation round.
- The bet_id column is an identifier for each bet in the current simulation round.
- The player_id column contains a player_id column value that must correspond to one of the players in the players table.
- The bet_type column contains a string value denoting either of two bet types in the simulation for this tip: a “pass line” bet or a “don’t pass line” bet.
- The bet_amount column value is the amount of a bet.
- The bet_result column contains a string value of “win” or “lose” depending on whether the bet wins or loses in the current simulation round. This column is not populated until after the last dice roll in a simulation.
- The dice_rolls table has a separate row for each of the rolls by the shooter in the current simulation round. There are six columns in the dice_rolls table. There can be one or more rolls in a simulation round, and each roll is denoted by a row in the dice_rolls table.
- The roll_id is an identity value for the current roll in a simulation. If the shooter wins or loses on the first roll, there is just one row in the dice_rolls table.
- The shooter_id column value corresponds to the player_id from the players table for the current shooter.
- Columns die1 and die2 correspond to the first and second die in a dice roll. The values of die1 and die2 are in the range of integers values 1 through 6 for each of the sides of a hexagonal die. The number of rows in the dice_rolls table corresponds to the number of rolls that it takes for a shooter to either win or lose a simulation round.
- The total column is a persisted computed column value that is the sum of the face-up value for die1 and die2 in a roll.
- The sixth column, named roll_timestamp, is populated with the datetime value for the current roll.
Rules for the Simplified Casino Craps Simulation
The rules for the simplified casino craps simulation are implemented by SQL Server stored procedures:
- The place_bet stored procedure places a new bet in the bets table for a player for the current shooter. This stored procedure also reduces a player’s bankroll by the amount of the bet after placing the bet.
- The roll_dice stored procedure invokes the SQL RAND function for each die in a pair of dice for the current shooter. The value of each face-up die is inserted in the dice_rolls table with the player_id for the current shooter.
- The resolve_game stored procedure updates the simulation tables after a shooter either wins or loses a simulation round. This is a relatively complex stored procedure whose details will be described and revealed in the code review below.
Code Review for the Simplified Casino Craps Simulation
There are three steps in the code for implementing a simulation round. The following code steps display the code for implementing a simulation round. This code starts with a reference to the Simplified_Casino_Craps_Simulation database.
Step 1
The first step creates a fresh version of the tables for a simulation round. The role and design of each table is described in the “Elements of a Simplified Casino Craps Simulation” section. The first section also designates foreign key references between the player_id columns in the bets table and the player_id column in the players table, as well as between the shooter_id column in the dice_rolls table and the player_id column in the players section.
Step 2
The second step creates a fresh version of the stored procedures for enforcing the rules for completing a simulation round. The roll_dice procedure includes a waitfor delay statement to enforce a ten-millisecond delay between successive die assignments within a single dice roll. The delay between these two die assignments allows time for SQL Server to reseed the SQL RAND functions for each die in a pair of die assignments. Without this explicit delay, SQL Server has a way of repeating successive dice rolls during a simulation round in a way that makes them not random.
Step 3
The third step in the code section below specifies selected parameter values for completing a single simulation round and invokes the stored procedures for completing a simulation round with those parameters. Each execution of the full script below creates a fresh set of output for a single simulation round.
After displaying the code for each of the three steps, this tip section walks you through the output from the third step of a series of different simulation rounds. You can initiate a new simulation round by running the script below. Reviewing the output from these simulation rounds clarifies key behaviors controlled by the Monte Carlo simulation code.
use Simplified_Casino_Craps_Simulation;
-- step 1: drop existing tables (if they exist) and create fresh tables
if exists (select * from sys.objects where object_id = object_id('dbo.dice_rolls') and type = 'U')
begin
drop table dbo.dice_rolls;
end;
if exists (select * from sys.objects where object_id = object_id('dbo.bets') and type = 'U')
begin
drop table dbo.bets;
end;
if exists (select * from sys.objects where object_id = object_id('dbo.players') and type = 'U')
begin
drop table dbo.players;
end;
create table players (
player_id int primary key identity,
player_name nvarchar(50),
bankroll decimal(10,2) check (bankroll >= 0)
);
create table bets (
bet_id int primary key identity,
player_id int foreign key references players(player_id),
bet_type nvarchar(20) check (bet_type in ('pass line', 'don’t pass line')),
bet_amount decimal(10,2),
bet_result nvarchar(10)
);
create table dice_rolls (
roll_id int primary key identity,
shooter_id int foreign key references players(player_id),
die1 int check (die1 between 1 and 6),
die2 int check (die2 between 1 and 6),
total as (die1 + die2) persisted,
roll_timestamp datetime default getdate()
);
-- step 2: drop existing stored procedures (if they exist) and create fresh stored procedures
if exists (select * from sys.objects where object_id = object_id('dbo.roll_dice') and type = 'P')
begin
drop procedure dbo.roll_dice;
end;
if exists (select * from sys.objects where object_id = object_id('dbo.place_bet') and type = 'P')
begin
drop procedure dbo.place_bet;
end;
if exists (select * from sys.objects where object_id = object_id('dbo.resolve_game') and type = 'P')
begin
drop procedure dbo.resolve_game;
end;
go
-- roll_dice procedure: simulates a dice throw using die1 and die2 and returns the result
-- use abs(checksum(newid)) instead of rand() to avoid duplicate sequential dice roll total values
create procedure roll_dice @shooter_id int
as
begin
declare @die1 int, @die2 int;
-- Calculate each die's value independently
set @die1 = floor(rand()*6)+1
-- WAITFOR DELAY statement allows time
-- for SQL Server to reseed rand()
-- between die assignments
WAITFOR DELAY '00:00:00.010'
set @die2 = floor(rand()*6)+1;
insert into dice_rolls (shooter_id, die1, die2)
values (@shooter_id, @die1, @die2);
select top 1 die1, die2, total
from dice_rolls
where shooter_id = @shooter_id
order by roll_timestamp desc;
end;
go
-- place_bet procedure: deducts the bet amount from the player's bankroll and inserts a bet record
create procedure place_bet @player_id int, @bet_type nvarchar(20), @bet_amount decimal(10,2)
as
begin
if (select bankroll from players where player_id = @player_id) >= @bet_amount
begin
update players
set bankroll = bankroll - @bet_amount
where player_id = @player_id;
insert into bets (player_id, bet_type, bet_amount)
values (@player_id, @bet_type, @bet_amount);
end;
end;
go
-- resolve_game procedure: handles the come-out roll, point phase, and bet resolution
create procedure resolve_game @shooter_id int
as
begin
declare @first_roll int,
@current_roll int,
@point int;
-- retrieve the come?out roll (the earliest dice roll for this shooter)
select top 1 @first_roll = total
from dice_rolls
where shooter_id = @shooter_id
order by roll_timestamp asc;
-- immediate resolution on the come?out roll (no point established)
if @first_roll in (7, 11)
begin
update bets
set bet_result = case
when bet_type in ('pass line', 'come') then 'win'
when bet_type in ('don’t pass line', 'don’t come') then 'lose'
end
where bet_result is null;
end
else if @first_roll in (2, 3, 12)
begin
update bets
set bet_result = case
when bet_type in ('pass line', 'come') then 'lose'
when bet_type in ('don’t pass line', 'don’t come') then 'win'
end
where bet_result is null;
end
else
begin
-- establish the point and continue rolling until resolution
set @point = @first_roll;
set @current_roll = 0;
while @current_roll <> 7 and @current_roll <> @point
begin
exec roll_dice @shooter_id;
select top 1 @current_roll = total
from dice_rolls
where shooter_id = @shooter_id
order by roll_timestamp desc;
end;
if @current_roll = @point
begin
update bets
set bet_result = case
when bet_type in ('pass line') then 'win'
when bet_type in ('don’t pass line') then 'lose'
end
where bet_result is null;
end
else if @current_roll = 7
begin
update bets
set bet_result = case
when bet_type in ('pass line', 'come') then 'lose'
when bet_type in ('don’t pass line', 'don’t come') then 'win'
end
where bet_result is null;
end;
end;
-- update player bankrolls based on resolved bets (winning bets pay double the wager)
update players
set bankroll = bankroll + (
select isnull(sum(bet_amount * case when bet_result = 'win' then 2 else 0 end), 0)
from bets
where bets.player_id = players.player_id
)
where player_id in (select player_id from bets where bet_result is not null);
end;
go
-- step 3: run simulation example
-- initialize player names and starting bankroll values
-- insert three players
insert into players (player_name, bankroll) values ('Mary', 100.00);
insert into players (player_name, bankroll) values ('Don', 100.00);
insert into players (player_name, bankroll) values ('Charlie', 100.00);
-- display initial player bankrolls
select 'before any dice rolls' as [Player Bankrolls]
select player_id, player_name, bankroll from players
-- place bets for game play scenario
-- Mary, the shooter, places a pass line bet in the amount of 10.00
-- Don places a dont't pass line bet in the amount of 10.00
-- Charlie places a don't pass line bet in the amount of 20.00
-- only place a bet if the player's bankroll is sufficient
if (select bankroll from players where player_id = 1) >= 10
exec place_bet @player_id = 1, @bet_type = 'pass line', @bet_amount = 10.00; -- Mary
-- only place a bet if the player's bankroll is sufficient
if (select bankroll from players where player_id = 2) >= 10
exec place_bet @player_id = 2, @bet_type = 'don’t pass line', @bet_amount = 10.00; -- Don
-- only place a bet if the player's bankroll is sufficient
if (select bankroll from players where player_id = 3) >= 20
exec place_bet @player_id = 3, @bet_type = 'don’t pass line', @bet_amount = 20.00; -- Charlie
-- display bets by player_id
select 'by player_id' [Bets]
select * from bets order by player_id
exec roll_dice @shooter_id = 2;
exec resolve_game @shooter_id = 2;
select 'at end of round' as [Player Bankrolls]
select * from playersFour results sets from step 3 are reviewed next to convey the types of results you can expect from running the preceding script to simulate four simulation rounds. I ran more than four simulations while I was searching for results sets like those that appear below.
- The top results set in the following screenshot details the player identifiers along with player names and bankrolls before any bets are placed in a simulation round. The player names and corresponding bankrolls are specified at the top of step 3 code.
- Next, three exec place_bets statements in step 3 place bets for players named Mary, Don, and Charlie. The select statement trailing the third exec place_bet statement displays the second results in the screen shots below. The outcomes in the second results set are from before any dice rolls or subsequent bankroll adjustments from game resolutions. This is why the bet_result column contains three NULL values.
- The third results set is from after the exec roll_dice statement. In this outcome, there is a single roll with a total value of 11. When a player initially rolls either a total value of 7 or 11, the simulation ends on that roll with a win for the shooter, which is Mary in this case. The initial roll in a simplified casino craps game is known as the come-out roll.
- The fourth results set is from after the exec resolve_game statement. This statement updates the player bankrolls as a result of the 11 total roll value.
- Mary’s bankroll is increased by $10 from $100 to $110 after the first, or come-out, roll. This is because Mary placed a pass line bet for $10.
- Don’s and Charlie’s initial bankrolls are reduced by $10 and $20, respectively, because they placed don’t pass line bets.
- The fourth results set displays the adjusted bankrolls after the first simulation round is resolved by the exec resolve_game statement.
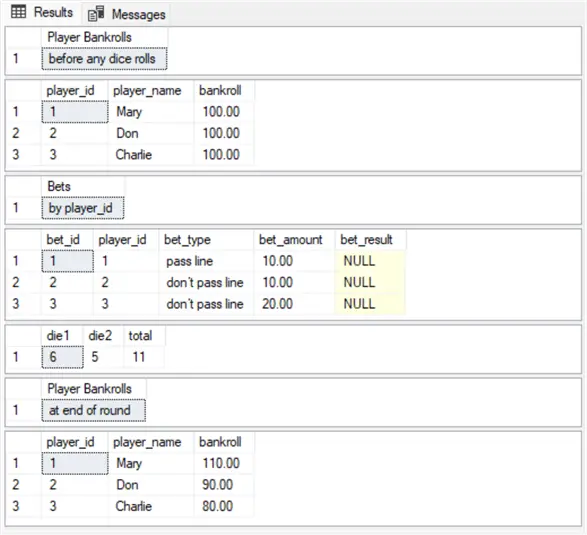
The results sets for a second simulation round appear below. The initial player bankrolls, the bet types, and the bet amounts are the same as in the preceding simulation round. As with the first simulation round, there is just one dice roll. However, the total value for the come-out roll for this simulation round is 12. This is one of three come-out total values (2, 3, and 12) that are typically referred to as craps. When the come-out total value is one of the craps total values, the pass line bet loses. In contrast, the simplified casino craps rules implemented within this tip cause don’t pass line bets to win for any of the three craps total values on the come-out roll. Therefore, Mary loses $10 from her initial bankroll, but Don and Charlie increase their initial bankrolls by $10 and $20, respectively, in the second simulation round. The simplified rules are both easier to follow and to code than for the standard casino craps game.
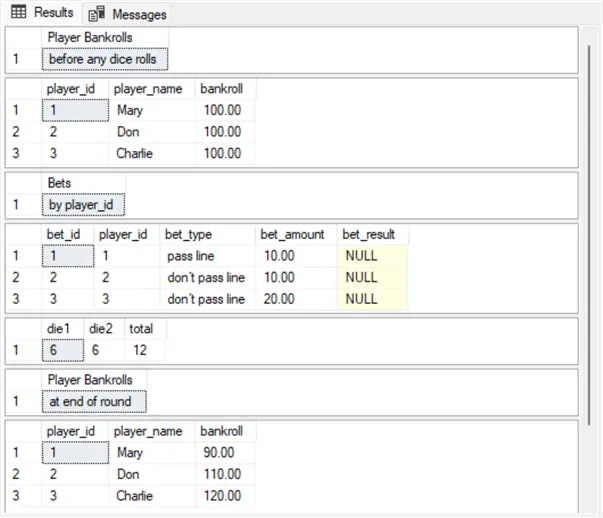
The results sets for a third simulation round appear next. Again, the initial player bankrolls and bet types are the same as the preceding two simulation rounds. However, for this third simulation round example, there are three dice rolls with successive total values of 8, 6, and 8.
A come-out total value of 4, 5, 6, 8, 9, or 10 sets a point total value that can result in a win for pass line bets if the shooter rolls the point value in a subsequent roll before rolling a 7. Because the pass line bet wins when point values are rolled a second time before a 7, don’t pass line bets lose. If a 7 is rolled in a subsequent dice roll before the point value, then the pass line bets lose, and don’t pass line bets win.
Because the point value of 8 is set in the come-out roll below, and the third roll is also an 8 with an intervening roll of 6, the pass line bet wins and the don’t pass line bet loses. Consequently, Mary’s bankroll increases by $10, and Don’s and Charlie’s bankrolls drop by $10 and $20, respectively, in the fourth result of the screenshot below.
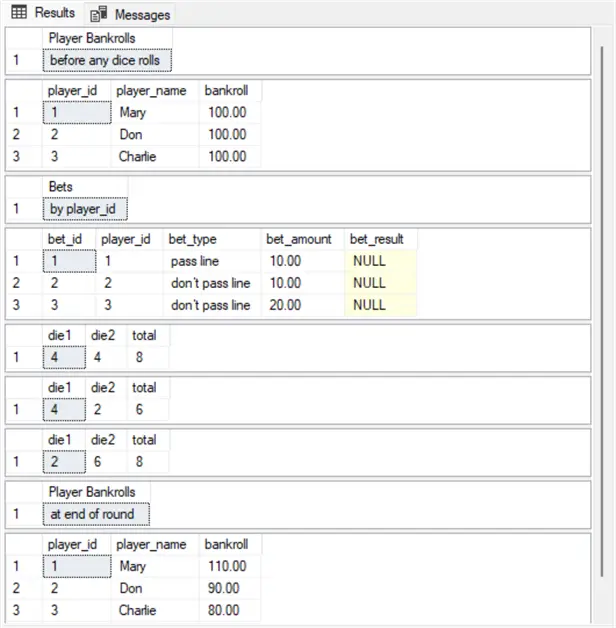
The next screenshot shows the results sets for another simulation round with a point value of 8. However, in this simulation round a 7 total value is rolled before rolling a second point value. Consequently, players with a pass line bet have their bankroll reduced by the amount of their bet. On the other hand, players with a don’t pass line bet have their bankroll increased by the amount of their bet.
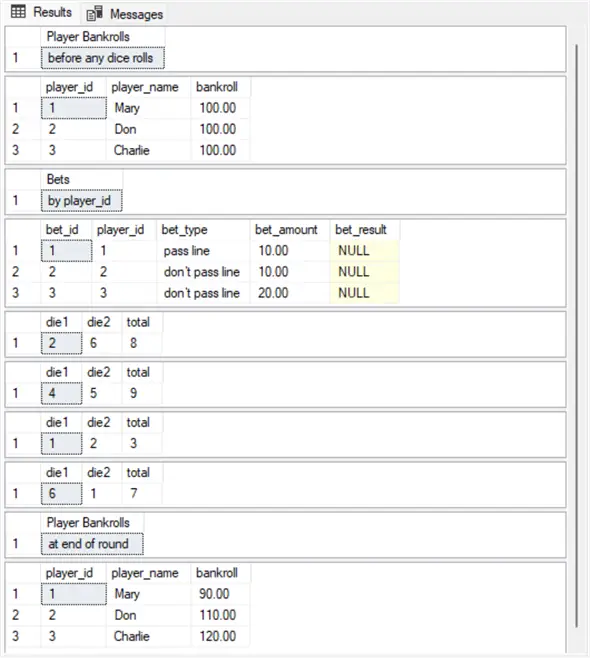
Carrying Bankrolls Forward Across Multiple Simulation Rounds
The examples in the preceding section all started with a fresh set of initial player bankrolls for each simulation round. This convention highlights how sets of one or more dice rolls within a simulation round can transform player bankrolls. However, in a normal casino craps game, player bankrolls carry forward between rounds of craps. Therefore, a win in the prior simulation round translates to a larger starting bankroll in the current simulation round. Similarly, a loss in the prior simulation round means a smaller starting bankroll in the current simulation round. In fact, in any Monte Carlo simulation analysis, you are likely to need to track outcomes, such as player bankrolls for the start of each round, across multiple simulation rounds.
This carrying forward feature can be implemented by replacing step 3 from the simulation code in the preceding section with the step 3 code in this section. The step 3 code for this section is described and revealed below.
- The @round local variable is for tracking the current simulation round number in a while loop within the step 3 code.
- The @maxRounds local variable sets a limit for the maximum number of simulation rounds to complete in step 3. You can determine this value by trial and error. You should seek an @maxRounds local variable value that yields relatively stable values for the last simulation round across sets of @maxRounds simulation rounds.
- Next, the following code excerpt assigns values to the players table. The main change here is that the starting balance is increased from $100 to $200 to accommodate the larger number of simulation rounds in the step 3 code for this section versus the preceding section.
- The first major block of code within the while loop invokes the place_bets procedure for each of the players.
- The bet amounts are the same for each player_id – namely, $10. The bet amounts were not the same for each player in the simulation rounds from the preceding section.
- The bet types vary. Mary and Charlie have the same bet types as in the preceding section, but the bet type for Don changes from don’t pass line in the preceding section to pass line in the current section.
- Next, the code designates Mary as the shooter.
- Then, the while loop code rolls the dice and resolves the game to establish a fresh set of player bankrolls based on the current simulation round. These actions result in a reset of the player bankrolls based on successive dice roll outcomes from @round equals one through @round equals one hundred.
- Next, the bets and dice_rolls tables are cleared for the next simulation round.
- The next to the last step in the while loop displays the updated players table with its revised bankrolls from the dice rolls in the current simulation round.
- Finally, the @round local variable is incremented by one.
- At the top of the while loop, the incremented value of the @round local variable is compared to the @maxRounds local variable value. Another simulation round is commenced so long as @round value is less than or equal to the @maxRounds local variable value.
-- step 3: Perform @maxRounds simulation rounds. Carry the refreshed bankrolls forward between rounds.
-- assume that the tables and stored procedures (roll_dice, place_bet, resolve_game)
-- have already been created (see previous section’s integrated example)
declare @round int = 1
declare @maxRounds int = 100;
-- initialize player names and starting bankroll values
-- insert three players
delete players
insert into players (player_name, bankroll) values ('Mary', 200.00);
insert into players (player_name, bankroll) values ('Don', 200.00);
insert into players (player_name, bankroll) values ('Charlie', 200.00);
-- display initial player bankrolls
select 'before any rounds' as [Player Bankrolls]
select player_id, player_name, bankroll from players
while @round <= @maxRounds
begin
-- only place a bet if the player's bankroll is sufficient
if (select bankroll from players where player_id = 1) >= 10
exec place_bet @player_id = 1, @bet_type = 'pass line', @bet_amount = 10.00; -- Mary
if (select bankroll from players where player_id = 2) >= 10
exec place_bet @player_id = 2, @bet_type = 'pass line', @bet_amount = 10.00; -- Don
if (select bankroll from players where player_id = 3) >= 10
exec place_bet @player_id = 3, @bet_type = 'don’t pass line', @bet_amount = 10.00; -- Charlie
-- have a shooter (for example, Mary with player_id = 1) do the come?out roll;
-- the subsequent rolls (if necessary) will be controlled within resolve_game
exec roll_dice @shooter_id = 1;
-- resolve the game based on the come?out roll, including any point phase
exec resolve_game @shooter_id = 1;
-- For simulation clarity, clear the bets and dice_rolls tables so the next round is a fresh start.
delete from bets;
delete from dice_rolls;
-- display player bankrolls for current round
-- with a 'no column name' header for 'Round # Player Bankrolls'
select 'Round ' + cast(@round as varchar(5)) as [Player Bankrolls]
select * from players
-- increase @round by 1
set @round = @round + 1;
endThe following screenshot shows the players table from before the first simulation round through the end of the second simulation round.
- The first player table shows that each player begins with a bankroll of $200.
- The come-out roll for the first simulation round has a total value of 7. Therefore, Mary and Don both have their bankroll values increase to $210, but Charlie has his bankroll value decrease to $190.
- During the second simulation round, Mary, the shooter, does not roll a second point value of 9 before rolling a 7. Therefore, the bankroll values for all three players revert to $200 – going up by $10 for Charlie and down by $10 for Mary and Don.
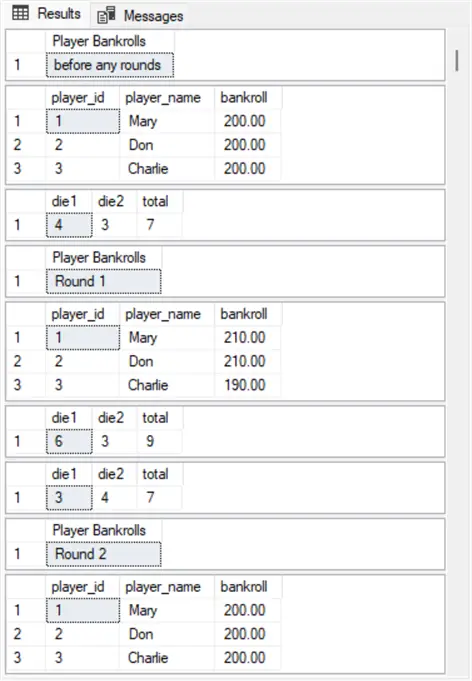
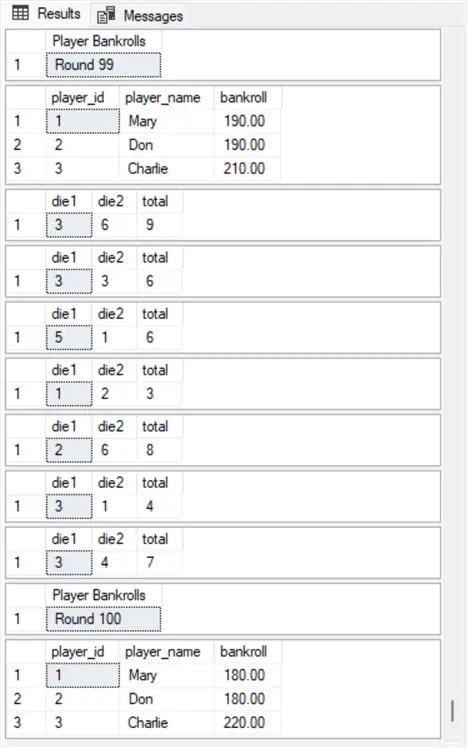
The next screenshot shows the players table at the end of rounds 99 and 100. In round 100, the shooter does not roll its point value of 9 before rolling a 7. Consequently, the bankroll values for Mary and Don decrease to $180 at the end of round 100. In contrast, the don’t pass line bet for Charlie grows his bankroll from $210 at the end or round 99 to $220 at the end of round 100.
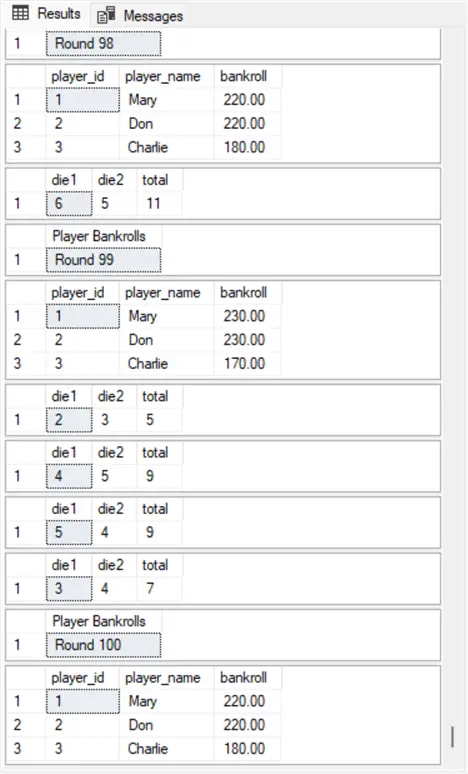
The next screenshot shows the players table for rounds 98, 99, and 100 in the second set of 100 simulation runs. In these example rounds, players Mary and Don have larger bankrolls for round 100 than Charlie. This is the reverse of the preceding of 100 rounds.
Next Steps
This tip introduces Monte Carlo simulations, using casino craps as a practical example to model stochastic phenomena. Through clear, hands-on demonstrations in T-SQL within SQL Server, you’ll see how Monte Carlo methods can provide a more intuitive and adaptable approach to solving complex problems than traditional mathematical models.
Although implementing a simplified craps simulation may not be a challenge for most readers, it serves as an accessible, easy-to-follow example of Monte Carlo modeling. By working through the examples, you’ll gain a solid foundation to apply these principles to more intricate models—ones that truly challenge you.
If you can verbally describe a process, chances are you can program it using the concepts in this guide—without needing deep expertise in mathematics or quantitative analysis. Dive in, explore the examples, and start leveraging Monte Carlo methods to tackle complex problems with confidence!


