Problem
Is it possible to have the DBSCAN algorithm in SQL Server without the use of external tools? If so, can you please provide a working example?
Solution
Let’s dive into some terms to set the ground work for the remainder of this DBSCAN algorithm in SQL Server tip.
Terms and definitions
DBSCAN
Density-Based Spatial Clustering of Applications with Noise algorithm is a density-based clustering non-parametric algorithm. It is robust to outliers, works well in nested clusters, well-suited for data with irregular shapes, and it is not necessary to specify the number of clusters. The limitations to find the optimal parameters can be challenging, it struggles when clusters have significantly different densities, and performance can degrade in high-dimensional spaces. The main uses are for anomaly detection, spatial data analysis, biological data analysis, and others.
Border point
Points that are near core points but lack enough neighbors to become a core point.
Cluster
Defined as a maximum set of density-connected points that are more similar to each other than those in other groups. Region where data points are closely packed together.
Core point
A core point has a sufficient number of neighbors within a specified EPS. Core points bring their friends to a cluster.
Density connectivity
Two points are density-connected if there is another point that both are density-reachable from it.
Density reachability
If two points are within a certain distance (EPS) of each other and also within a dense region.
EPS (Epsilon)
Define the radius of the neighborhood around a data point as such as if the distance between two points is less than or equal to EPS, then they are considered neighbors. Choosing the right value for it is important once if it is too small most points will be classified as noise and if eps is too large cluster may merge and the algorithm may fail to distinguish them. It essentially creates a radius around each point.
MinPts (Minimum points)
This is the minimum number of points required within the eps radius to form a dense region. As a general rule of thumb set the MinPts as the number of dimensions plus one with a minimum value of three.
Noise point (outlier)
Point that does not belong to any cluster. It is not a core and it is not reachable from core.
Supervised learning
A framework in machine learning where algorithms learn patterns exclusively on labeled data to make predictions or classifications.
Unsupervised learning
A framework in machine learning where algorithms learn patterns exclusively from unlabeled data to make predictions or classifications.
DBSCAN in SQL Server
This algorithm classifies each point as core, border, or outlier. The working phases are:
- Arbitrarily select a point p
- Retrieve all points density-reachable from p regarding to its EPS and MinPts:
- If p is a core point, a cluster is formed
- If p is a border point, no points are density-reachable from p, and DBSCAN visits the next point
- Continue the process until all points have been processed.
The computational complexity is O.(n^2) and if using spatial index then O.(n.Log(n)).
Tables
The first table will hold your input data to be processed
CREATE TABLE [dbo].[DbscanData](
[PointId] [int] IDENTITY(1,1) NOT NULL,
[X] [float] NOT NULL,
[Y] [float] NOT NULL,
[ClusterId] [int] NULL,
[PointType] [char](1) NULL,
[Neighbors] [int] NULL,
[SpatialPoint] AS ([geometry]::Point([x],[y],(0))),
CONSTRAINT [PK_DbscanData] PRIMARY KEY CLUSTERED
(
[X] ASC,
[Y] ASC
)WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE = OFF, IGNORE_DUP_KEY = OFF, ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON, OPTIMIZE_FOR_SEQUENTIAL_KEY = OFF) ON [PRIMARY]
) ON [PRIMARY]
GOThe second table will hold the neighbors of each point of your input data
CREATE TABLE [dbo].[DbscanDataNeighbors](
[Point] [int] NOT NULL,
[Neighbor] [int] NOT NULL,
[Neighbors] [int] NULL,
[Cluster] [smallint] NULL,
[Changed] [bit] DEFAULT 0,
[Distance] [float] NULL,
CONSTRAINT [PK_DbscanDataNeighbors] PRIMARY KEY CLUSTERED
(
[Point] ASC,
[Neighbor] ASC
)WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE = OFF, IGNORE_DUP_KEY = OFF, ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON, OPTIMIZE_FOR_SEQUENTIAL_KEY = OFF) ON [PRIMARY]
) ON [PRIMARY]
GODBSCAN stored procedure
The stored procedure needs to have in advance the values of epsilon and the minimum points to be considered as a core point.
USE [MsSqlTips]
GO
/****** Object: StoredProcedure [dbo].[uspDBSCAN] Script Date: 12/06/2025 13:21:17 ******/
SET ANSI_NULLS ON
GO
SET QUOTED_IDENTIFIER ON
GO
-- =============================================
-- Author: SCP - MSSQLTips
-- Create date: 20250609
-- Description: DBSCAN clustering
-- =============================================
ALTER PROCEDURE [dbo].[uspDBSCAN]
(@Epsilon decimal(18,6)
,@MinPts int)
WITH EXECUTE AS CALLER
AS
BEGIN
SET NOCOUNT ON;
IF (SELECT COUNT(*) FROM [dbo].[DbscanData]) < 1
RETURN;
BEGIN TRY
DECLARE @MaxLoop int
,@Exit int = 0
,@Cluster int = 0
,@Neighbor int
,@Point int;
DECLARE @List
TABLE (Pt int);
UPDATE [dbo].[DbscanData]
SET [PointType] = NULL
,[ClusterId] = NULL
,[Neighbors] = NULL;
-- If you work only with Euclidian distance you can use
-- P1.SpatialPoint.STDistance(P2.SpatialPoint) <= (@Epsilon))
UPDATE P1
SET [Neighbors] =
(SELECT COUNT(P2.pointid) + 1
FROM [dbo].[DbscanData] AS P2
WHERE P1.PointId <> P2.PointId AND
SQRT(POWER(P1.X - P2.X, 2) + POWER(P1.Y - P2.Y, 2)) <= (@Epsilon))
FROM [dbo].[DbscanData] AS P1;
UPDATE [dbo].[DbscanData]
SET [PointType] = 'N'
WHERE [Neighbors] = 1;
UPDATE [dbo].[DbscanData]
SET [PointType] = 'C'
WHERE [Neighbors] >= @MinPts;
TRUNCATE TABLE [dbo].[DbscanDataNeighbors];
INSERT INTO [dbo].[DbscanDataNeighbors]
([Point]
,[Neighbor]
,[Neighbors]
,[Distance])
SELECT P1.PointId
,P2.PointId
,P1.Neighbors
,SQRT(POWER(P1.X - P2.X, 2) + POWER(P1.Y - P2.Y, 2))
FROM [dbo].[DbscanData] AS P1 JOIN
[dbo].[DbscanData] AS P2 ON
P1.PointId <> P2.PointId AND
SQRT(POWER(P1.X - P2.X, 2) + POWER(P1.Y - P2.Y, 2)) <= (@Epsilon);
SET @MaxLoop = (SELECT COUNT(*) * 2
FROM [dbo].[DbscanDataNeighbors]);
WHILE EXISTS
(SELECT 1
FROM [dbo].[DbscanDataNeighbors]
WHERE [Cluster] IS NULL OR
[Changed] = 1) BEGIN
IF NOT EXISTS
(SELECT 1
FROM [dbo].[DbscanDataNeighbors]
WHERE [Changed] = 1) BEGIN
SET @Cluster += 1;
SELECT TOP 1 @Point = [Point]
,@Neighbor = [Neighbor]
FROM [dbo].[DbscanDataNeighbors]
WHERE [Cluster] IS NULL;
UPDATE [dbo].[DbscanDataNeighbors]
SET [Cluster] = @Cluster
,[Changed] = 1
WHERE ([Point] = @Point AND
[Neighbor] = @Neighbor);
END
DELETE FROM @List;
INSERT INTO @List
SELECT DISTINCT [Point]
FROM [dbo].[DbscanDataNeighbors]
WHERE [Changed] = 1
INSERT INTO @List
SELECT DISTINCT [Neighbor]
FROM [dbo].[DbscanDataNeighbors]
WHERE [Changed] = 1 AND NOT EXISTS
(SELECT 1
FROM @List
WHERE Pt = [Neighbor]);
UPDATE [dbo].[DbscanDataNeighbors]
SET [Changed] = 0
WHERE [Changed] = 1;
UPDATE [dbo].[DbscanDataNeighbors]
SET [Cluster] = @Cluster
,[Changed] = CASE WHEN [Neighbors] < @MinPts THEN 0 ELSE 1 END
WHERE [Point] IN (SELECT Pt FROM @List) AND
[Cluster] IS NULL;
SET @Exit += 1;
IF @Exit > @MaxLoop
BREAK;
END
UPDATE [dbo].[DbscanData]
SET [ClusterId] = NULL;
WITH cteChk (CId,Cn) AS
(SELECT [Cluster]
,COUNT(DISTINCT POINT) N
FROM [dbo].[DbscanDataNeighbors]
GROUP BY [Cluster])
UPDATE [dbo].[DbscanDataNeighbors]
SET [Cluster] = NULL
FROM cteChk
WHERE [Cluster] = CId AND
Cn < @MinPts;
WITH CteCluster (PId, CId) AS
(SELECT [Point]
,[Cluster]
FROM [dbo].[DbscanDataNeighbors]
GROUP BY [Point],[Cluster])
UPDATE [dbo].[DbscanData]
SET [ClusterId] = CId
FROM CteCluster
WHERE [PointId] = PId;
-- ====================================================
-- Adjusting the radius of a circle around each point
DECLARE @OverallExtent geometry
,@ProportionalBuffer float;
SELECT @OverallExtent = geometry::EnvelopeAggregate([SpatialPoint])
FROM [dbo].[DbscanData];
DECLARE @MinX float = @OverallExtent.STPointN(1).STX;
DECLARE @MinY float = @OverallExtent.STPointN(1).STY;
DECLARE @MaxX float = @OverallExtent.STPointN(3).STX;
DECLARE @MaxY float = @OverallExtent.STPointN(3).STY;
DECLARE @ExtentWidth float = @MaxX - @MinX;
DECLARE @ExtentHeight float = @MaxY - @MinY;
DECLARE @MinDimension float = IIF(@ExtentWidth < @ExtentHeight, @ExtentWidth, @ExtentHeight);
DECLARE @Ratio float = @MinDimension * 0.02;
-- Returning the clusters
SELECT [ClusterId]
,COUNT(*) AS N
,geometry::CollectionAggregate(SpatialPoint) AS geom
FROM (SELECT ClusterId
,CASE
WHEN ClusterId IS NULL THEN SpatialPoint.STBuffer(@Ratio / 2)
WHEN PointType = 'C' THEN SpatialPoint.STBuffer(@Ratio * 1.2)
ELSE SpatialPoint.STBuffer(@Ratio * 0.75 )
END AS SpatialPoint
FROM [dbo].[DbscanData]) AS X
GROUP BY [ClusterId];
END TRY
BEGIN CATCH
IF @@TRANCOUNT > 0
BEGIN
ROLLBACK TRANSACTION;
END
-- Print error information.
PRINT 'Error: ' + CONVERT(varchar(50), ERROR_NUMBER()) +
', Severity: ' + CONVERT(varchar(5), ERROR_SEVERITY()) +
', State: ' + CONVERT(varchar(5), ERROR_STATE()) +
', Procedure: ' + ISNULL(ERROR_PROCEDURE(), '-') +
', Line: ' + CONVERT(varchar(5), ERROR_LINE());
PRINT ERROR_MESSAGE();
END CATCH;
ENDExamples
Simple graph
TRUNCATE TABLE [dbo].[DbscanData];
INSERT INTO [dbo].[DbscanData]
([X],[Y])
VALUES (1,1),(2,3),(1,2),(2,2),(3,5)
,(3,9),(2,6),(4,7),(4,8),(4,9)
,(7,6),(7,9),(7,5),(9,4),(7,4)
,(8,4),(6,3),(7,3),(8,3),(7,2);
DECLARE @Epsilon decimal(18,6) = 2
,@MinPts int = 4;
EXEC [dbo].[uspDBSCAN] @Epsilon,@MinPts;Returns 3 clusters and 3 noise points
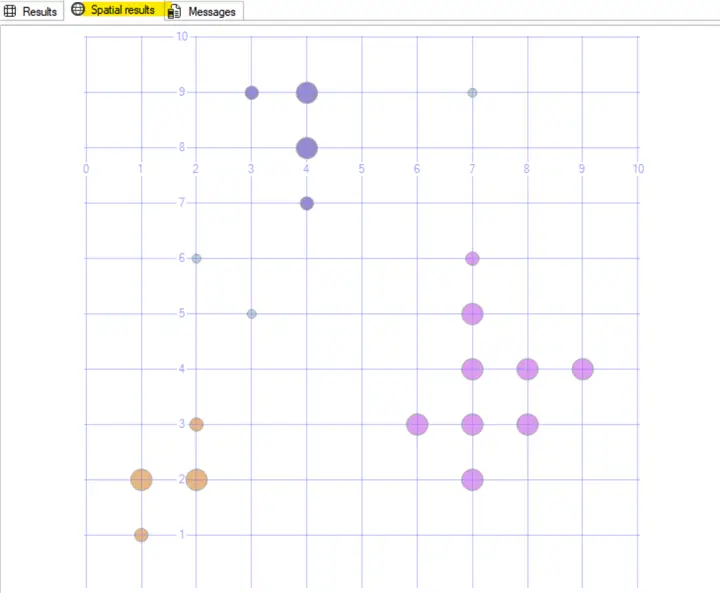
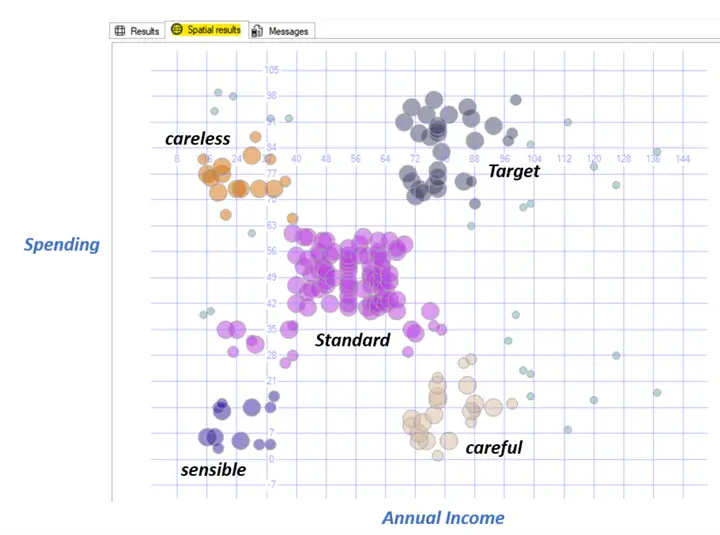
Mall customers example
There is a common data file example in the internet called Mall_Customers.csv which I downloaded, then truncate the table DbscanData, and inserted in the X column the Annual Income and in the Y column the Spending Score distinct values and execute the following:
DECLARE @Epsilon decimal(18,6) = 10
,@MinPts int = 7;
EXEC [dbo].[uspDBSCAN] @Epsilon,@MinPts;Results
Which resulted in 5 clusters and 25 outliers. Analyzing the distribution of the cluster we can assume a feature for each one, like:
Next Steps
There are a lot of improvements to be done on this, I would like to point out the following:
- The cluster Id has number to identify them but it is not in strict sequence order.
- Report server can done a better job to show the graph but using the Spatial Results tab is practical.
- After running observe the size, density, and distribution of the clusters obtained and try to change the epsilon and min points values to improve it. Also put attention to the identified noises to observe if it makes sense.
- There are some useful methods to find the good epsilon value and It is a good procedure to assess the quality of the clustering based on the data, allowing to automate the process of best fit values.
- DBSCAN is an unsupervised algorithm and then you do not have true labels to compare against.
- Create profile clusters gaining insights about what are the common characteristics of points within a cluster, based on your domain knowledge.
- If you have a lot of dimensions, you can use the dimensionality reduction techniques, like Linear Discriminant Analysis (LDA) which is a supervised method that aims to find the projection that best separates the classes in the data, and Principal Component Analysis (PCA) which is an unsupervised method that aims to find the directions of maximum variance in the data.
More information can be found at:


