Box Muller Transform: Generate Random Numbers with SQL

Problem

Generating random numbers from a normal distribution is essential for accuracy and realistic modeling, simulation, inference, and algorithm design. This is useful for scientific, engineering, statistical, and AI domains. Let’s see how we can create Box Muller transform functionality in SQL Server without the use of external tools.

Solution

It is a common necessity to have data to test functions for:

Modeling natural phenomena: Measurements of errors, sensor noise in signal processing, financial returns, and test scores.
Simulations: Weather and climate modeling, risk analysis in finance, reliability tests, and stock prices simulations.
Machine learning: Weight initialization in neural networks, Bayesian models, and Gaussian mixture models.
Statistical inference and testing of hypotheses.
Randomization algorithms.
Physics and engineering.

Random Gaussian Numbers in SQL using Box-Muller Transform

The Box-Muller transform takes two independent uniform random numbers (0,1) and maps them to two independent standard normal random variables, having mean zero and standard deviation of one.

The first step is to generate the number of rows desired with random numbers for the columns defined. Then we can do the following.

From the random number one, we calculate the first normally distributed variable, using the formula:

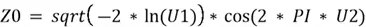
And for the second normally distributed variable, using the formula:

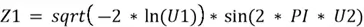
Let’s see how we can build this in SQL Server.

Generated Numbers Table

First we will create a table to store the data.

-- MSSQLTips (TSQL)
 
CREATE TABLE [dbo].[RndNormalDist](
    [ClusterId] [int] NOT NULL,
    [PointId] [int] NOT NULL,
    [X] [float] NOT NULL,
    [Y] [float] NOT NULL,
    [SpatialPoint]  AS ([geometry]::Point([x],[y],(0))),
 CONSTRAINT [PK_RndNormalDist] PRIMARY KEY CLUSTERED 
(
    [ClusterId] ASC,
    [PointId] ASC
)WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE = OFF, IGNORE_DUP_KEY = OFF, ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON, OPTIMIZE_FOR_SEQUENTIAL_KEY = OFF) ON [PRIMARY]
) ON [PRIMARY]
GO

Box-Muller Stored Procedure

This is the stored procedure for the Box-Muller Transform.

-- =============================================
-- Author:      SCP - MSSQLTips
-- Create date: 20250716
-- Description: Normal Box-Muller Transform
-- =============================================
CREATE OR ALTER PROCEDURE [dbo].[uspRandGenBoxMuller] 
                (@Points int
                ,@X_Offset decimal(18,6)
                ,@Y_Offset decimal(18,6)
                ,@Scale decimal(18,6)
                ,@ClusterId int)
WITH EXECUTE AS CALLER 
AS
BEGIN;
 
    BEGIN TRY
 
        DECLARE             @GenPoints     
            TABLE        ([PointId] int IDENTITY(1,1)
                        ,[X] decimal(18, 6)
                        ,[Y] decimal(18, 6));
 
        WITH Numbers AS 
            (SELECT      1 AS n
    
             UNION ALL
    
             SELECT      n + 1
                FROM     Numbers
                WHERE    n < @Points),
             RandomPairs AS 
            (SELECT      n
                        ,RAND(CHECKSUM(NEWID())) AS U1
                        ,RAND(CHECKSUM(NEWID())) AS U2
                FROM     Numbers)
        INSERT INTO      @GenPoints 
                        ([X]
                        ,[Y])
            SELECT       @X_Offset + @Scale * (SQRT(-2 * LOG(rp.U1)) * COS(2 * PI() * rp.U2))
                        ,@Y_Offset + @Scale * (SQRT(-2 * LOG(rp.U1)) * SIN(2 * PI() * rp.U2))
                FROM     RandomPairs rp
                OPTION  (MAXRECURSION 0);
 
        SELECT             [PointId]
                        ,[X]
                        ,[Y]
                        ,@ClusterId
            FROM         @GenPoints;
 
        RETURN;
    END TRY
    BEGIN CATCH
        PRINT    'Error: ' + CONVERT(varchar(50), ERROR_NUMBER()) +
                ', Severity: ' + CONVERT(varchar(5), ERROR_SEVERITY()) +
                ', State: ' + CONVERT(varchar(5), ERROR_STATE()) + 
                ', Procedure: ' + ISNULL(ERROR_PROCEDURE(), '-') + 
                ', Line: ' + CONVERT(varchar(5), ERROR_LINE());
        PRINT ERROR_MESSAGE();
    END CATCH;
END
GO

If you need more variables, you can add more offset parameters and its respective lines for the calculation and also the return point in the SELECT clause for the temporary table.

Generating Random Numbers

Let’s generate a group of six random clusters. We will do an INSERT and insert the results from the stored procedure execution. Below, we are creating 6 cluster groups.

The parameters for the stored procedure are:

number of points
x offset value
y offset value
scale
and the cluster number.

-- MSSQLTips (TSQL)
 
TRUNCATE TABLE [dbo].[RndNormalDist];
 
-- Cluster 1
INSERT INTO  [dbo].[RndNormalDist]
            ([PointId]
            ,[X]
            ,[Y]
            ,[ClusterId])
    EXEC [dbo].[uspRandGenBoxMuller] 250,-5,-2,0.8,1;
 
-- Cluster 2
INSERT INTO  [dbo].[RndNormalDist]
            ([PointId]
            ,[X]
            ,[Y]
            ,[ClusterId])
    EXEC [dbo].[uspRandGenBoxMuller] 250,5,6,2,2;
 
-- Cluster 3
INSERT INTO  [dbo].[RndNormalDist]
            ([PointId]
            ,[X]
            ,[Y]
            ,[ClusterId])
    EXEC [dbo].[uspRandGenBoxMuller] 250,4,-1,0.1,3;
 
-- Cluster 4
INSERT INTO  [dbo].[RndNormalDist]
            ([PointId]
            ,[X]
            ,[Y]
            ,[ClusterId])
    EXEC [dbo].[uspRandGenBoxMuller] 250,1,-2,0.2,4;
 
-- Cluster 5
INSERT INTO  [dbo].[RndNormalDist]
            ([PointId]
            ,[X]
            ,[Y]
            ,[ClusterId])
    EXEC [dbo].[uspRandGenBoxMuller] 250,-2,3,0.3,5;
    
-- Cluster 6
INSERT INTO  [dbo].[RndNormalDist]
            ([PointId]
            ,[X]
            ,[Y]
            ,[ClusterId])
    EXEC [dbo].[uspRandGenBoxMuller] 250,3,-2,1.6,6;
 
-- Returning the generated values
SELECT       [ClusterId]
            ,[PointId]
            ,[X]
            ,[Y]
            ,[SpatialPoint]
    FROM     [dbo].[RndNormalDist];
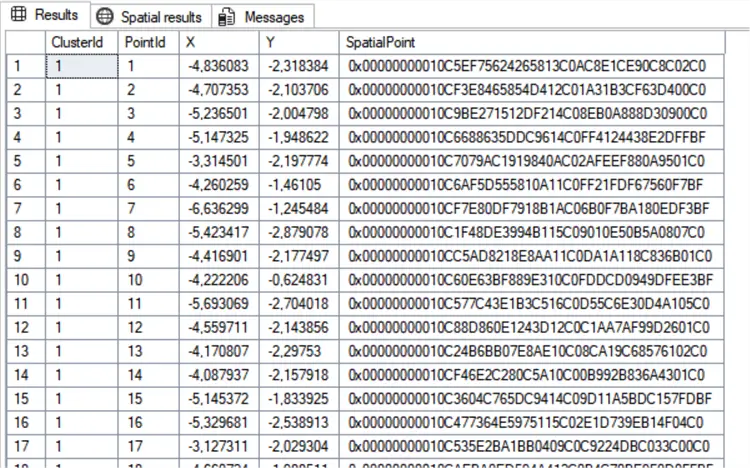
GO

Resulting in:

Visual the Data with Spatial Results

If you want to have a better visualization using the Spatial Results tab, you can use the following:

-- MSSQLTips (TSQL)
 
DECLARE  @OverallExtent geometry
        ,@ProportionalBuffer float;
        
SELECT       @OverallExtent = geometry::EnvelopeAggregate([SpatialPoint])
    FROM     [dbo].[RndNormalDist];
 
DECLARE @MinX float = @OverallExtent.STPointN(1).STX;
DECLARE @MinY float = @OverallExtent.STPointN(1).STY;
DECLARE @MaxX float = @OverallExtent.STPointN(3).STX;
DECLARE @MaxY float = @OverallExtent.STPointN(3).STY;
 
DECLARE @ExtentWidth float = @MaxX - @MinX;
DECLARE @ExtentHeight float = @MaxY - @MinY;
 
DECLARE @MinDimension float = IIF(@ExtentWidth < @ExtentHeight, @ExtentWidth, @ExtentHeight);
 
DECLARE @Ratio float = @MinDimension * 0.015; 
 
        -- Returning the clusters
 
SELECT       [ClusterId]
            ,COUNT(*) AS N
            ,geometry::CollectionAggregate(SpatialPoint) AS geom
    FROM    (SELECT      [ClusterId]
                        ,SpatialPoint.STBuffer(@Ratio)  AS SpatialPoint
                FROM     [dbo].[RndNormalDist]) AS X
            GROUP BY [ClusterId];
GO

Resulting in:

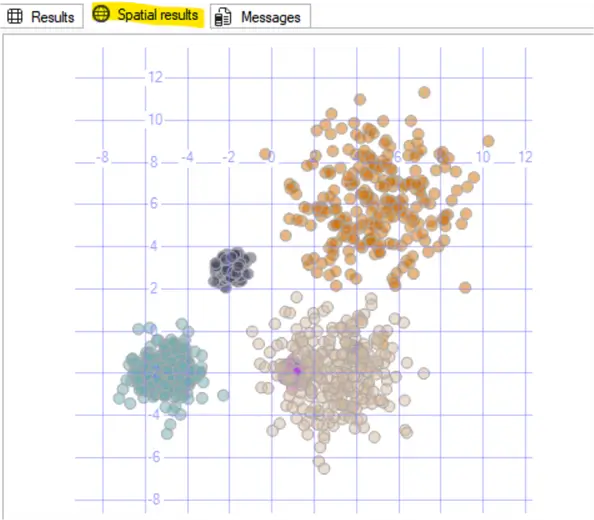
Next Steps

WIKIPEDIA – Box Muller transform
Check out more TSQL related articles

Resources

Community

Subscribe

Random Gaussian Numbers in SQL using Box-Muller Transform