Problem
It is very usual to have a set of discrete data points but sometimes it is necessary to estimate values between those points. Is it possible to create a function to do this in SQL Server?
Solution
Among other methods, the Lagrange interpolation is a numerical method used to find a polynomial that passes exactly through a given set of points. It is commonly used in engineering, data interpolation, signal processing, image resampling, numerical solutions of differential equations, control system, robotics, trajectory planning in computer graphics and animation, etc.
It is indicative for a relatively small number of points once higher degree polynomials have a problem of oscillation at the edges of an interval.
Lagrange Interpolation Table Value Function
I created a user defined table type to work with the x and y data.
CREATE TYPE [dbo].[uttTwoVar] AS TABLE(
[n] [int] IDENTITY(1,1) NOT NULL,
[x] [decimal](18, 6) NULL,
[y] [decimal](18, 6) NULL
)In addition, I created a Lagrange function that uses the data type above to enter the table of x and y values, the number of interpolated items that I want to retrieve OR the increment steps between the minimum and maximum x.
-- =============================================
-- Author: SCP - MSSQLTips
-- Create date: 20241104
-- Description: Lagrange Interpolation
-- =============================================
CREATE FUNCTION [dbo].[tvfLagrangeInterpolation]
(@Data dbo.uttTwoVar READONLY
,@Itens int
,@Delta decimal(18,6))
RETURNS @DataRes TABLE
([n] int
,[x] decimal(18, 6)
,[y] decimal(18, 6))
WITH EXECUTE AS CALLER
AS
BEGIN
DECLARE @n decimal(18,6)
,@nMax decimal(18,6) = (SELECT MAX(n) FROM @Data)
,@vh decimal(18,8)
,@pod decimal(18,8)
,@pol decimal(18,8)
,@p decimal(18,6)
,@xMin decimal(18,6) = (SELECT MIN(x) FROM @Data);
IF @Itens > 0
BEGIN
SET @n = @Itens - 1;
SET @vh = ((SELECT MAX(x) FROM @Data) - @xMin) / @n;
END
ELSE
BEGIN
SET @vh = @Delta;
SET @n = ((SELECT MAX(x) FROM @Data) - @xMin) / @vh;
END
DECLARE @L int = 1
,@vi int
,@vk int
,@xi decimal(18,6)
,@xk decimal(18,6);
WHILE @L <= @n + 1
BEGIN
SET @p = @xMin + @vh * (@L -1);
SET @pol = 0;
SET @vk = 1
WHILE @vk <= @nMax
BEGIN
SET @xk = (SELECT x FROM @Data WHERE n = @vk);
SET @pod = 1;
SET @vi = 1
WHILE @vi <= @nMax
BEGIN
SET @xi = (SELECT x FROM @Data WHERE n = @vi)
IF @vi <> @vk
SET @pod *= (@p - @xi) / (@xk - @xi)
SET @vi += 1;
END
SET @pol += (SELECT y FROM @Data WHERE n = @vk) * @pod
SET @vk += 1;
END
INSERT INTO @DataRes
SELECT @L
,@p
,@pol;
SET @L += 1;
END
RETURN;
ENDExecuting the Lagrange Interpolation Function
So, we can now run the example code below to use the function.
DECLARE @Data [dbo].[uttTwoVar];
INSERT INTO @Data
VALUES ( 1, 1)
,( 3, 9)
,( 5, 25)
,(10, 100);
SELECT * FROM [dbo].[tvfLagrangeInterpolation] (@Data,0,1);The data followed the equation y = x2 to easily verify the interpolated values with an increment step of 1, resulting in:
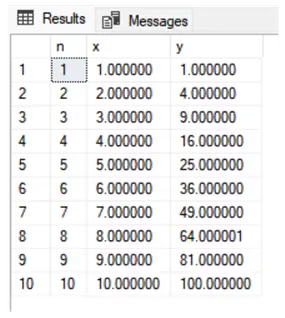
Lagrange Interpolation Example
In addition, I decided to enter a number and its logarithmic value.
DECLARE @Data [dbo].[uttTwoVar];
INSERT INTO @Data
VALUES (1.00,LOG(1))
,(1.25,LOG(1.25))
,(1.50,LOG(1.5))
,(1.75,LOG(1.75))
,(2.00,LOG(2))
,(2.25,LOG(2.25))
,(2.50,LOG(2.5))
,(2.75,LOG(2.75))
,(3.00,LOG(3));
SELECT *, FORMAT(EXP(y),'0.0000') AS ExpChk FROM [dbo].[tvfLagrangeInterpolation] (@Data,0,0.125);We can now see that executing the code we have the values of y and the EXP(y) check column:

There is no need to know the previous equation behind the data, and I only did this to better illustrate that the interpolated values follow the rule. The precision will depend on the number of points entered.
Next Steps


