Problem
How do you calculate the distance between two different points on a sphere using TSQL in SQL Server? In this article, we look at how this can be done to calculate different points on the globe.
Solution
Let’s start off with some terms and definitions before we dive into an example of how to determine distance between two points.
Terms and Definitions
Here are some terms to be familiar with as we calculate the distance between two points with SQL code:
Great Circle Navigation (Orthodromic)
A Great Circle route is the shortest path between two points on the surface of a sphere. It is the path traced when a plane cuts through the center of the Earth, forming a circle with the same radius as the Earth itself. In navigation, following a Great Circle route allows a vessel or aircraft to cover the shortest distance between two points to minimize travel distance in turn reduce fuel consumption and travel time. This is particularly beneficial for long-distance flights and oceanic voyages. It requires constant heading adjustment due to the curvature of the earth and needs precise navigation systems to make frequent course corrections.
Rhumb Line Navigation (Loxodrome)
A Rhumb Line is a path that crosses all meridians (longitudinal lines) at the same angle. Unlike the Great Circle, a Rhumb Line is not the shortest path between two points, but it maintains a constant bearing. This results in a spiral pattern that theoretically reaches the poles. It is easier to follow using traditional navigational tools like compasses and making navigation straightforward.
Degrees
They are units for measuring angles, where a full circle is divided into 360 degrees. Each degree is divided into 60 minutes, and each minute is divided into 60 seconds.
Radians
They are units for measuring angles where a full circle is 2* π radians, which is approximately 6.283 radians.
Mean Radius of the Earth
The mean radius is approximately 6,371 km. However, for more precise calculations, the equatorial radius is 6,378 km and the Polar radius is 6,357 km.
Conversions
| Calculation | Formula |
|---|---|
| Degrees to Radians | Multiply by π/180 |
| Radians to Degrees | Multiply by 180/π |
| Nautical Miles to Km | Multiply by 1.852 |
| Km to Nautical Miles | Multiply by 0.53996 |
| Miles to Km | Multiply by 1.60934 |
| Km to Miles | Multiply by 0.62137 |
| Nautical Miles to Miles | Multiply by 1.15078 |
| Miles to Nautical Miles | Multiply by 0.868976 |
Setting Up Test Data in SQL Server
To work with real data, I suggest downloading the International Air Transport Association’s (IATA) listing of airport codes using the following link: IATA Airport List.
There are a lot of ways to upload to a table in SQL Server and I decided to use the Import Flat File method.

I named the table AIRPORTS. The only change I made was to the latitude and longitude columns, changing its data type to nvarchar(10) to avoid problems with the decimal using a dot, since my system uses a comma as the decimal separator.
Table to Hold Airports Data
CREATE TABLE [dbo].[Airports](
[country_code] [nvarchar](2) NULL,
[region_name] [nvarchar](50) NULL,
[iata] [nvarchar](3) NULL,
[icao] [nvarchar](4) NULL,
[airport] [nvarchar](100) NULL,
[latitude] [nvarchar](10) NULL,
[longitude] [nvarchar](10) NULL
) ON [PRIMARY]
GOCreate the Function to Normalize Degrees in Decimal Degrees
-- =============================================
-- Author: SCP - MSSQLTips
-- Create date: 20241024
-- Description: Normalize to decimal Degrees
-- =============================================
CREATE FUNCTION [dbo].[ufnConvToDecDegrees]
(@Dms varchar(100))
RETURNS decimal(18,6)
AS
BEGIN
DECLARE @Degrees decimal(18,6);
DECLARE @cleanDms varchar(100) = '';
DECLARE @i int = 1;
DECLARE @currentChar char(1);
WHILE @i <= LEN(@Dms)
BEGIN
SET @currentChar = SUBSTRING(@Dms, @i, 1);
IF @currentChar LIKE '[0-9NSEW .,]'
BEGIN
SET @cleanDms = @cleanDms + @currentChar;
END
IF @currentChar LIKE '[°′″´'']'
BEGIN
SET @cleanDms = @cleanDms + ' ';
END
SET @i = @i + 1;
END
SET @Dms = REPLACE(@cleanDms,' ',' ');
DECLARE @Table TABLE
(Item int Identity(0,1)
,ItemValue decimal(18,8));
INSERT INTO @Table
(ItemValue)
SELECT value
FROM string_split(@Dms,' ')
WHERE ISNUMERIC(value) = 1;
UPDATE @Table
SET ItemValue = ItemValue / POWER(60,Item);
SELECT @Degrees = SUM(ItemValue) *
(CASE WHEN @Dms LIKE '%W%' OR
@Dms LIKE '%S%'
THEN -1
ELSE 1
END)
FROM @Table;
RETURN @Degrees;
ENDCreate the Table Value Function to Obtain Distance and Bearing
-- =============================================
-- Author: SCP - MSSQLTips
-- Create date: 20241024
-- Description: Great Circle Distance
-- =============================================
CREATE FUNCTION [dbo].[tvfGreatCircleDist]
(@StrLat1 varchar(20)
,@StrLong1 varchar(20)
,@StrLat2 varchar(20)
,@StrLong2 varchar(20))
RETURNS @Dist TABLE
(lat1 decimal(18,6)
,long1 decimal(18,6)
,lat2 decimal(18,6)
,long2 decimal(18,6)
,km decimal(18,6)
,mi decimal(18,6)
,nmi decimal(18,6)
,bearing decimal(18,6))
WITH EXECUTE AS CALLER
AS
BEGIN
IF ISNUMERIC(@StrLat1) = 0
SET @StrLat1 = [dbo].[ufnConvToDecDegrees] (@StrLat1);
IF ISNUMERIC(@StrLong1) = 0
SET @StrLong1 = [dbo].[ufnConvToDecDegrees] (@StrLong1);
IF ISNUMERIC(@StrLat2) = 0
SET @StrLat2 = [dbo].[ufnConvToDecDegrees] (@StrLat2);
IF ISNUMERIC(@StrLong2) = 0
SET @StrLong2 = [dbo].[ufnConvToDecDegrees] (@StrLong2);
DECLARE @Lat1 decimal(18,6) = RADIANS(@StrLat1);
DECLARE @Long1 decimal(18,6) = RADIANS(@StrLong1);
DECLARE @Lat2 decimal(18,6) = RADIANS(@StrLat2);
DECLARE @Long2 decimal(18,6) = RADIANS(@StrLong2);
DECLARE @DeltaLat decimal(18,6) = @Lat2 - @Lat1;
DECLARE @DeltaLong decimal(18,6) = @Long2 - @Long1;
DECLARE @D decimal(18,6) = ACOS(SIN(@Lat1) * SIN(@Lat2) + COS(@Lat1) * COS(@Lat2) * COS(@DeltaLong)) * 6371;
DECLARE @Bear decimal(18,6) = ATN2((SIN(@DeltaLong) * COS(@Lat2)),(COS(@Lat1) * SIN(@Lat2) - SIN(@Lat1) * COS(@Lat2) * COS(@DeltaLong)));
SET @Bear = (DEGREES(@Bear) + 360) % 360;
INSERT INTO @Dist
VALUES (DEGREES(@Lat1)
,DEGREES(@Long1)
,DEGREES(@Lat2)
,DEGREES(@Long2)
,@D
,@D * 0.621371
,@D * 0.539957
,@Bear);
RETURN;
END
Testing the SQL Code
Here are some tests to see if the function is working as planned to calculate the distance between two points in SQL code.
Calculate Distance from New York (US) to São Paulo (BR) with SQL Code
To enter angles other than decimals, enter the numbers and letters (N, S, E, W) always separated by a space like ’40 38 23 N’ or symbol like ’40°38´23″N’.
SELECT * FROM [dbo].[tvfGreatCircleDist] ('40°38´23"N','73°46´44"W','23°26′08″S','46°28′23″W');
GOThe result will be 7,663 km or 4,762 miles, bearing 153.2 degrees.
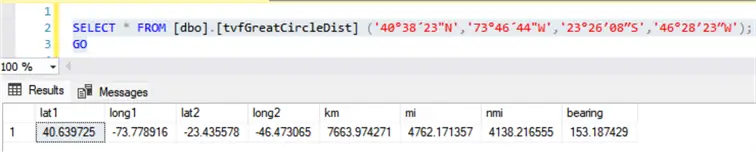
Let’s check if this is correct by visiting FCC – Distance and Azimuths Between Two Sets of Coordinates.

Using the Airport Data
Search the IATA airport codes in the downloaded table AIRPORTS by querying the airport column.
DECLARE @Airport1 nvarchar(3) = 'JFK';
DECLARE @Airport2 nvarchar(3) = 'NRT';
DECLARE @AirpName1 nvarchar(100)
DECLARE @AirpName2 nvarchar(100)
DECLARE @Lat1 decimal(18,6)
,@Long1 decimal(18,6)
,@Lat2 decimal(18,6)
,@Long2 decimal(18,6);
SELECT @Lat1 = [latitude]
,@Long1 = [longitude]
,@AirpName1 = [airport]
FROM [dbo].[Airports]
WHERE [iata] = @Airport1;
SELECT @Lat2 = [latitude]
,@Long2 = [longitude]
,@AirpName2 = [airport]
FROM [dbo].[Airports]
WHERE [iata] = @Airport2;
SELECT CONCAT(@AirpName1,' (',lat1,',',long1,')') AS [Origin]
,CONCAT(@AirpName2,' (',lat2,',',long2,')') AS [Destination]
,km
,mi
,nmi
,bearing
FROM [dbo].[tvfGreatCircleDist] (@Lat1,@Long1,@Lat2,@Long2);This results in 10,830 km bearing 332 degrees.

Let’s check if this is correct by visiting FCC – Distance and Azimuths Between Two Sets of Coordinates.

Playing with Geometry to Visualize the Route
Add the following code to the bottom of the above query and do the calculation for JFK to GRU airport.
SET @Lat1 = RADIANS(@Lat1);
SET @Long1 = RADIANS(@Long1);
SET @Lat2 = RADIANS(@Lat2);
SET @Long2 = RADIANS(@Long2);
DECLARE @DeltaLat numeric(18,6) = @Lat2 - @Lat1;
DECLARE @DeltaLong numeric(18,6) = @Long2 - @Long1;
DECLARE @Route TABLE
(Item int IDENTITY
,Lat decimal(18,6)
,Long decimal(18,6)
,GeoLoc geography);
DECLARE @Count int = 0
,@Inc int = 25;
WHILE @Count <= @Inc
BEGIN
INSERT INTO @Route
(Lat
,Long)
VALUES (@Lat1
,@Long1);
SET @Lat1 += @DeltaLat / @Inc;
SET @Long1 += @DeltaLong / @Inc;
SET @Count += 1;
END;
UPDATE @Route
SET GeoLoc = geography::Point(Lat, Long, 4326)
,Lat = DEGREES(Lat)
,Long = DEGREES(Long);
DECLARE @lineString NVARCHAR(MAX) = 'LINESTRING(';
SELECT @lineString = @lineString + CAST(Long AS VARCHAR(20)) + ' ' + CAST(Lat AS VARCHAR(20)) + ', '
FROM @Route
ORDER BY Item;
SET @lineString = LEFT(@lineString, LEN(@lineString) - 2) + ')';
DECLARE @geoLine geometry;
SET @geoLine = geometry::STGeomFromText(@lineString, 0);
SELECT @geoLine;This will give the route that can be viewed in the Spatial results tab.
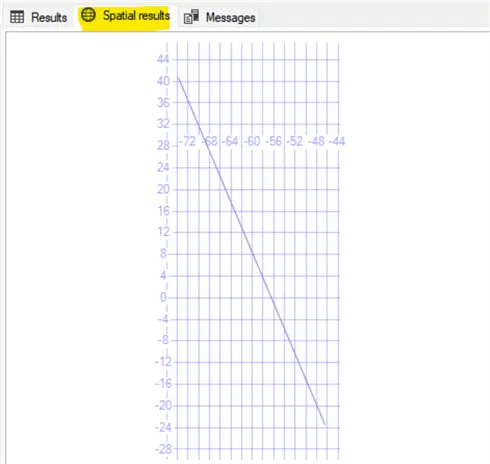
I have a table called Countries that contains geometric shapes saved in the column geom for each country. Then, I changed the SELECT @geoline line to:
SELECT @geoLine
UNION ALL
SELECT geom
FROM [dbo].[Countries]
WHERE geom IS NOT NULL AND
MacroReg IN ('AMERICA');This will provide a little better visualization at the Spatial results tab.
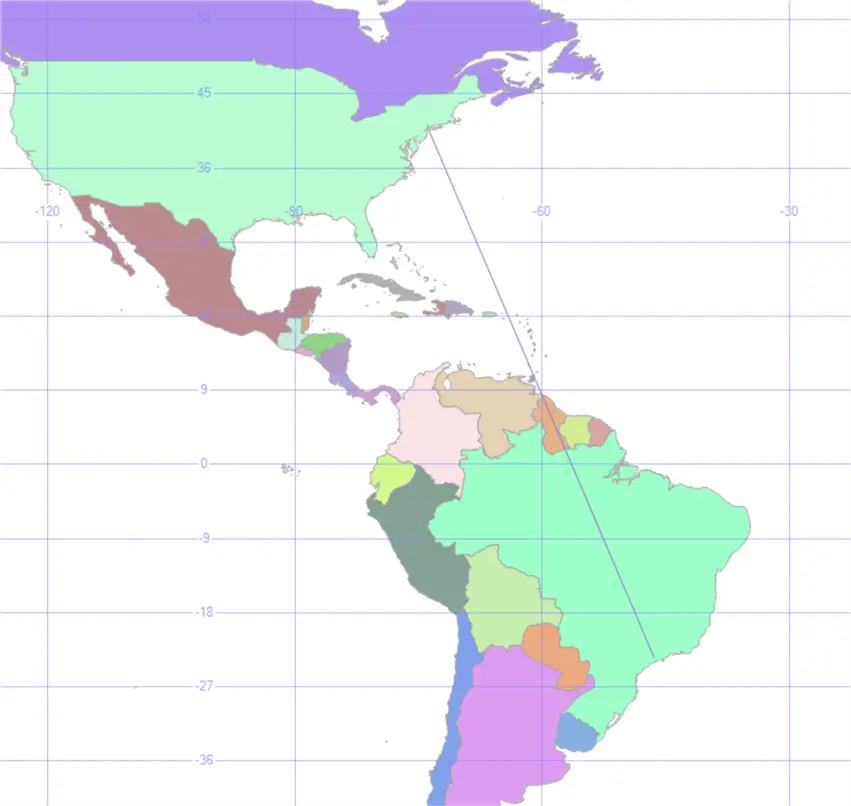
Nearest Airport
The latitude and longitude of Midlothian, Virginia (US) is 37° 30′ 21″ N and 77° 38′ 56″ W. To find the nearest airports, you can run the following code:
DECLARE @StrLat1 nvarchar(20) = '37° 30´ 21" N'
,@StrLong1 nvarchar(20) = '77° 38´ 56" W';
IF ISNUMERIC(@StrLat1) = 0
SET @StrLat1 = [dbo].[ufnConvToDecDegrees] (@StrLat1);
IF ISNUMERIC(@StrLong1) = 0
SET @StrLong1 = [dbo].[ufnConvToDecDegrees] (@StrLong1);
DECLARE @Lat decimal(18,6) = RADIANS(@StrLat1);
DECLARE @Long decimal(18,6) = RADIANS(@StrLong1);
SELECT TOP (10) [country_code]
,[region_name]
,[iata]
,[icao]
,CONCAT([airport],' (',[latitude],',',[longitude],')') AS [airport]
,ROUND(6371 * ACOS(SIN(@lat) * SIN(RADIANS([latitude])) + COS(@lat) * COS(RADIANS([latitude])) * COS(RADIANS([longitude]) - @Long)),2) Km
FROM [dbo].[Airports]
ORDER BY Km;Resulting in:

Next Steps
Check out these additional resources:


