Using T-SQL to find the shortest distance between two points

By: Eli Leiba   |   Comments (4)   |   Related: > TSQL

Problem

This tip shows how to determine the shortest path of a weighted graph problem with the help of some elements from the T-SQL language.  The weighted graph problem is a classic and interesting problem that is usually presented in computer science academic courses. In graph theory, the shortest path problem is the problem of finding a path of two vertices (or nodes) start and end, in a graph such that the sum of the weights of its constituent edges is minimized (from Wikipedia).

There are several well documented algorithms for this problem. Algorithms like: Bellman-Ford, Dijkstra, Topological Sorting, The Floyd-Warshall algorithm, the Johnson's algorithm and more.  See this link for more info: https://brilliant.org/wiki/shortest-path-algorithms/.

The values of each node in the graph are called its "weight" and can be considered as the “cost” or the "distance" of the node. This value is attached to all the edges of the graph. The solution to this problem is finding the shortest or minimal path in the graph, that is, to show a way to go from a starting node to the ending node with the minimal cost or distance.

There are many scenarios where this algorithm comes handy. Here are some common scenarios:

• Finding the shortest path of two cities connected by a "graph" of different roads, each road has a different distance.
• Finding the shortest path of two streets addresses connected by a "graph" of different streets, each street has a different street length.
• Finding the shortest distance and path of devices, for two start and end communication devices (like routers or controllers) connected by a "graph" of other devices. 

In this tip, I will show a T-SQL alternative to these algorithms that deals with this problem with the aid of a common table expression recursive query and the rank window function.

Solution

For the solution, I will create a simple table and populate it with the "graph" vertices.

Here is the table structure and some sample content, representing a graph of connected cities A, B, C, D, and E. Each city is connected to each other with a network of roads as shown below.

CREATE TABLE Graph (
   PA VARCHAR (5), 
   PB VARCHAR (5), 
   Distance INT
   ) 
GO
 
INSERT INTO Graph VALUES 
(NULL, 'A', 0), 
('A', 'B', 4), 
('A', 'C', 7), 
('B', 'C', 10), 
('C', 'D', 15), 
('B', 'D', 17), 
('A', 'D', 23), 
('B', 'E', 22), 
('C', 'E', 29) 
GO 

The drawing of the graph is something like this:

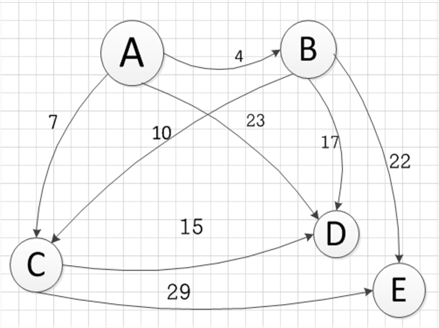
Here is a summary of the process.

• The procedure, named dbo.usp_FindShortestGraphPath gets the two nodes as input parameters. @start and @end.
• The procedure uses a recursive common table expression query in order to get all the possible paths of roads @start point and @end point.
• The first part of the CTE queries the @start point; the recursive part constructs the paths to each node and sums up all the distances between each pair of nodes in the path as the total distance of the path.
• The path constructed will be printed as N1-N2-N3……Nn
• In the final part of the procedure, I use the Rank() window function in order to find the rank of the total distance between each path and show only the path ranking first. (Rank = 1). This is also the shortest distance path solution.

Here is the T-SQL code for the stored procedure

-- ==============================================================
-- Author:      Eli Leiba
-- Create date: 24-05-2018
-- Description: finding the shortest distance path between two 
--              different points "p-start" and "p-end" in a graph (table presentation)
-- ===============================================================
CREATE PROCEDURE dbo.usp_FindShortestGraphPath (@strt VARCHAR (5), @end VARCHAR (5))
AS
BEGIN
   SET NOCOUNT ON;
   WITH CommonTableExp1
   AS (SELECT PB,
         CASE 
            WHEN PA IS NULL
               THEN CAST ('-' + ISNULL (PA, PB) + '-' AS VARCHAR (MAX))
            WHEN PA IS NOT NULL
               THEN CAST ('-' + PA + '-' + PB + '-' AS VARCHAR (MAX))
            END FullPath,
         Distance TotalDistance
      FROM Graph
      WHERE (PA = @strt)
      UNION ALL
      SELECT a.PB,
         c.FullPath + '-' + a.PB + '-' FullPath,
         TotalDistance + a.Distance TotDistance
      FROM Graph a, CommonTableExp1 c
      WHERE a.PA = c.PB
      ),
   CommonTableExp2
   AS (SELECT *, RANK () OVER (ORDER BY TotalDistance) TheRank
      FROM CommonTableExp1
      WHERE PB = @end AND PATINDEX ('%' + @end + '%', FullPath) > 0)
   SELECT FullPath, TotalDistance
   FROM CommonTableExp2
   WHERE TheRank = 1;
   SET NOCOUNT OFF
END
GO			

Here is an example using the procedure

For the above table and content – to find the shortest path from point A to point D, execute the procedure like this:

exec dbo.usp_FindShortestGraphPath 'A', 'D'

Here is the output:

FullPath              TotalDistance 
------------------    --------------- 
-A-B--D-              21 

The shortest path is from point A to B (4 km) and then from B to D (17 km), with a total distance of 21 km.

Next Steps

• You can create this simple procedure (and table) in your application database and use it as a tool for calculating the shortest path of any two points in a graph.
• The procedures were tested for SQL Server 2014 and 2017.
• The stored procedure should be compatible with SQL Server versions that support common table expression (CTE) recursive queries and the window ranking function.

About the author

Eli Leiba is a senior application DBA, a teacher and a senior database consultant with 19 years of RDBMS experience.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips