Exponential Moving Average Calculation in SQL Server

By: Rick Dobson   |   Updated: 2020-06-16   |   Comments (3)   |   Related: > TSQL

Problem

As our organization increases its use of time series data, the IT department is also getting more requests to compute and maintain exponential moving averages. Please demonstrate the basics of how to compute exponential moving averages for time series data. Also, present and describe the operation of a stored procedure for computing exponential moving averages for any period length. Additionally, include examples of how to save and retrieve exponential moving averages computed by the stored procedure.

Solution

Exponential moving averages have many data mining and modeling applications for time series data, including

• Smoothing changes in values over time to assess if values are generally trending up, down, or sideways
• Determining if recent value changes point to upward or downward momentum in the data values
• Predicting future values based on trends and short-term momentum moves

This tip starts with a spreadsheet-based tutorial on how to compute exponential moving averages. The tip presents and reviews a stored procedure for computing exponential moving averages based on any period length. The tip concludes with two sections on saving and retrieving exponential moving averages in SQL Server tables.

The equations for computing exponential moving averages

Exponential moving averages track changes for a metric over time. A metric can be anything that you are monitoring over time, such as the daily closing price of a stock or daily start-of-day free space versus start-of-day allocated space for your databases.

• Exponential moving averages are based on all values from the current period through to the beginning value in a time series.
• An exponential moving average applies different weights to a sequence of values in a time series. The weights for the most recent values are greater than the weights for less recent values.
• Exponential moving averages can be computed starting with the third period no matter how long the period length for a moving average is.

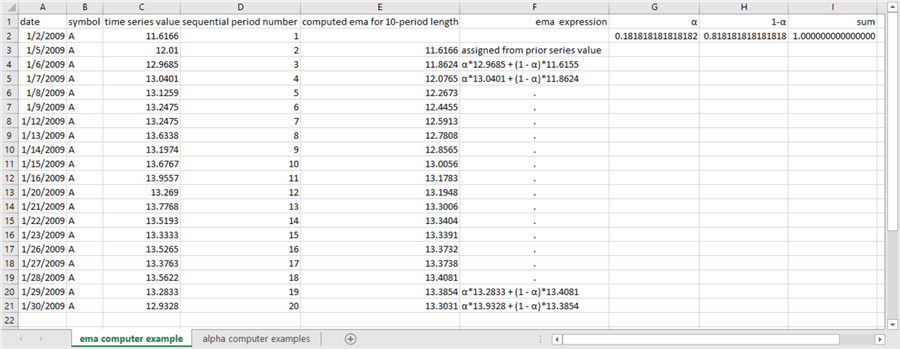
The following screen shot shows an Excel worksheet with sample computations for a ten-period exponential moving average.

• The dates for trading days in January 2009 appear in column A.
• The symbol representing a stock appear in column B.
• Stock closing prices appear in column C. This is the metric within this tip for which exponential moving averages are computed.
• Row numbers for successive time series values appear in column D. This spreadsheet includes stock closing prices for the twenty trading days in January during 2009.
• Exponential moving average values appear in column E for the closing prices in column C.
• The rules for assigning or computing exponential moving averages appear in column F. Not all authors prescribe exactly the same rules. The rules applied in this tip were previously published and demonstrated in the Engineering Statistics Handbook as well as in a prior tip on mining time series data with exponential moving averages.
  • There is never an exponential moving average for the first time series period, which is 1/2/2009 in the following spreadsheet.
  • The exponential moving average for the second time series period can be set equal to the time series value from the first period, such as 11.6166 from the value in cell C2 below. You always need a seed value before starting to compute exponential moving averages.
  • The expression in cell F4 is for the first computed exponential moving average value.
    • Notice this is for the third period.
    • The values of α and (1-α) are specified, respectively, in cells G2 and H2. This tip presents below a technique for deriving α values based on period length.
    • The most important point to note is that the computation of exponential moving average values is iterative, and it is also dependent on the sum of two different values.
      • The first value for rows 5 through 21 is α times the time series value for the current period.
      • The second value is (1 – α) times the exponential moving average from the prior period.

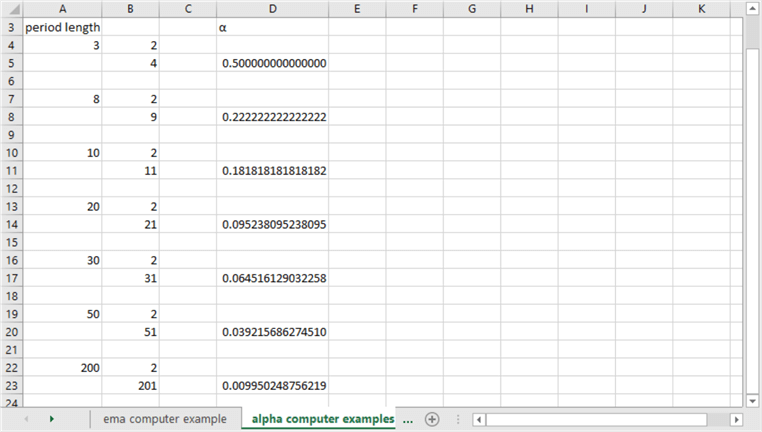
In financial applications, it is common to compute the value of α as two divided by the number of periods in a period length plus one for a set of exponential moving averages. The following screen shot shows the computation of α for the seven different period lengths used in this tip.

• The seven different periods used in this tip appear in column A.
• Column B contains the numerator and denominator for computing an α value.
  • For a period length of 3, the numerator for computing α is 2, and the denominator is 4 (period length plus one). The division of the numerator by the denominator should be carried out for fifteen places after the decimal point when you declare α as a float value in SQL Server.
  • When computing exponential moving averages with a two-hundred period length, the numerator and denominator values for computing α are, respectively, 2 and 201.
• Column D contains the computed α values for the period lengths in column A.

The data source for this tip

The data in the preceding section and the remainder of this tip are from a fact table of a time series data warehouse. A description of the warehouse appears in this prior tip. The fact table (yahoo_prices_valid_vols_only) resides in the dbo schema of a database named for_csv_from_python. This section presents a few queries for the fact table to acquaint you with the data source used in this tip. This tip assumes you have a table somewhat similar to the fact table used in this tip for your time series data or that you can configure your time series data to reflect the layout of the fact table used in this tip.

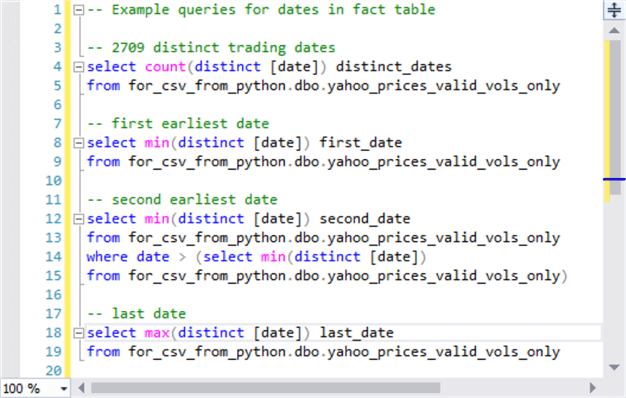
The following screen shot shows a script excerpt with a set of four queries for the dates in the fact table.

• The first script example counts the number of distinct dates in the fact table.
  • In general, a time series database will have a core set of distinct dates that are used repeatedly for different entities about which there are data over time. This tip tracks multiple stock symbols over time. Every entity may or may not have values for each distinct date.
  • This fact table has 2709 distinct dates. These dates are for days when US stock markets are open. This is generally Monday through Friday, excluding holidays, weekend days, and other special dates when stock markets are closed, such as for storms that severely restrict access to the stock market.
• The code examples in the following screen shot extract the earliest date, the second earliest date, and the last distinct date.

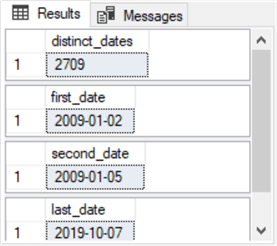
Here’s another screen shot with a result set for the preceding script segment.

• The first results set displays the count of distinct dates in the fact table.
• The second, third, and fourth results sets display, respectively, the first, second, and last distinct dates in the fact table.

Here’s another script excerpt that can display all distinct stock symbols in the fact table as well as the first set of twenty time series values for the symbol A used in the preceding example. As the comment for the first script example below indicates there are 2614 distinct symbols that have a close price for each distinct trading date in the fact table.

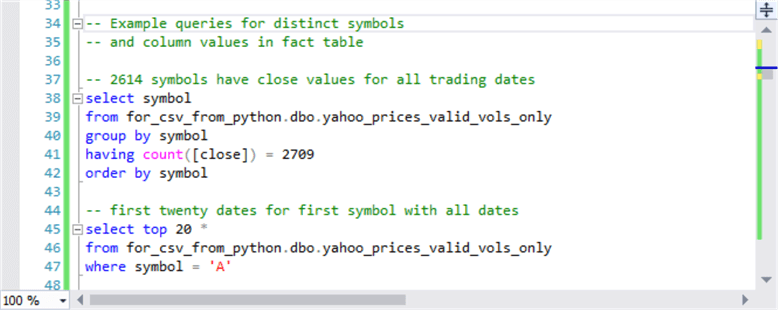
Here’s an excerpt from the results sets from the preceding script examples.

• The results set in the top window shows the first eight symbols from the set of 2614 symbols with trading days for all distinct dates in the fact table. The first symbol (A) is for the one used in the preceding section. The remaining symbols with trading days for all dates are after the eighth row.
• The results set in the bottom window shows the layout of the rows in fact table.
  • The sample rows are the twenty rows that include the sample data in the preceding section – namely, close prices for the stock symbol A in January during 2009.
  • Notice that there are time series values for other columns of data. For example, it is not uncommon to compute moving averages for daily close prices as well as volume data – namely, the number of stock shares traded on each date.

A stored procedure for computing exponential moving averages with any period length

The following script creates a fresh version of a stored procedure named usp_ema_computer in the for_csv_from_python database. The stored procedure assumes that source data for computing exponential moving averages are available from the yahoo_prices_valid_vols_only table in the dbo schema of the for_csv_from_python database. When working with data from another source, you will need to revise the stored procedure to point at the data source for which you wish to compute exponential moving averages.

• The use statement at the top of the script points at the source database with values on which to compute exponential moving averages.
• The script conditionally drops the usp_ema_computer stored procedure before commencing the creation of a fresh copy of the stored procedure.
• Three input parameters are required by usp_ema_computer.
  • @symbol is an identifier that designates a set of values for which to compute exponential moving averages. In this demonstration, moving averages are computed for close prices for the symbol designated by @symbol.
  • @period is an integer value that denotes the period length for which to compute exponential moving averages.
  • @alpha is a float value that represents the value of α from the "The equations for computing exponential moving averages" section. The section includes sample computations for computing α values for different period lengths.
• Next, the code extracts the first close price for the symbol specified by @symbol.
• Then, the code creates a fresh copy of the #temp_for_ema table. A fully populated version of the table is displayed with the computed exponential moving averages in the stored procedure’s last step.
  • The code block begins by removing any prior version of the #temp_for_ema table.
  • Then, a draft version of the table is populated via a select statement’s into clause from the source data table (yahoo_prices_valid_vols_only) and several expressions designated as list items.
    • date, [symbol], and [close] designate columns from the source data table.
    • [row_number] is a column of integer values populated by the row_number window function. The values start at one for the first period and increase by one for each subsequent period in the time series.
    • ema is assigned the first time series value (@ema_first). This value is initially defined in a preceding declare statement. The value for @ema_first is appropriate for the second row in the ema column of the #temp_for_ema table. The ema column value is redefined in subsequent code for other table rows.
    • A where clause in the select statement with the into #temp_for_ema clause extracts the time series values for the entity specified by the @symbol value.
    • An order by clause arranges rows sequentially by row_number value, which corresponds to date values (see the row_number window function specification).
• The next code block assigns a null value to ema for the first row in #temp_for_ema. Recall there is no exponential moving average for the initial row of the time series.
• Next, three declare statements specify and define values for some local variables for a while loop. The while loop computes fresh exponential moving average values for rows three through the last row of time series values.
  • The while loop iterates from rows three through the maximum row_number value.
  • For each iteration, the value of @today_ema is set equal to α times the current row’s time series value plus (1 – α) times the exponential moving average from the prior row.
  • Then, an update statement revises the ema value for the current row to the value of @today_ema.
• The last statement in the while loop increments the value of @current_row_number by one. When @current_row_number initially exceeds @max_row_number, control passes to the first statement after the while loop.
• The select statement after the while loop displays the values in #temp_for_ema. These values include the computed/assigned exponential moving averages, the original time series values, the dates, the identifier for the time series, and the period length for the moving averages.

use [for_csv_from_python]
go
 
-- conditionally drop a stored proc
if object_id('dbo.usp_ema_computer') is not null 
     drop proc dbo.usp_ema_computer
go
 
create procedure usp_ema_computer 
   -- Add the parameters for the stored procedure here
    @symbol nvarchar(10)  -- for example, assign as 'GOLD'
   ,@period int           -- for example, asssign as 10
   ,@alpha float       -- for example, assign as 2.0/(10 + 1)
as
 
begin
   -- suppress row counts for output from usp
   set nocount on;
 
   -- parameters to the script are
   -- @symbol identifier for set of time series values
   -- @period number of periods for ema
   -- @alpha weight for current row time series value
 
   -- initially populate #temp_for_ema for ema calculations
   -- @ema_first is the seed
   declare @ema_first money = 
   (select top 1 [close] from [dbo].[yahoo_prices_valid_vols_only] where symbol = @symbol order by [date])
 
   -- create base table for ema calculations
   begin try
   drop table #temp_for_ema
   end try
   begin catch
   print '#temp_for_ema not available to drop'
   end catch
 
   -- ema seed run to populate #temp_for_ema
   -- all rows have first close price for ema 
   select 
    [date]
   ,[symbol]
   ,[close]
   ,row_number() OVER (ORDER BY [Date]) [row_number]
   ,@ema_first ema
   into #temp_for_ema
   from [dbo].[yahoo_prices_valid_vols_only]
   where symbol = @symbol
   order by row_number
 
   -- NULL ema values for first period
   update #temp_for_ema
   set
    ema = NULL
   where row_number = 1
 
   -- calculate ema for all dates in time series
   -- @alpha is the exponential weight for the ema
   -- start calculations with the 3rd period value
   -- seed is close from 1st period; it is used as ema for 2nd period 
 
   -- set @max_row_number int and initial @current_row_number
   -- declare @today_ema
   declare @max_row_number int = (select max(row_number) from #temp_for_ema)  
   declare @current_row_number int = 3
   declare @today_ema float
 
   -- loop for computing successive ema values
   while @current_row_number <= @max_row_number
   begin
 
    set @today_ema =
    (
    -- compute ema for @current_row_number
    select 
    top 1
    ([close] * @alpha) + (lag(ema,1) over (order by [date]) * (1 - @alpha)) ema_today
 
    from #temp_for_ema
    where row_number >=  @current_row_number -1 and row_number <= @current_row_number
    order by row_number desc
    )
 
    -- update current row in #temp_for_ema with @today_ema
    -- and increment @current_row_number 
    update #temp_for_ema
    set 
     ema = @today_ema
    where row_number = @current_row_number
 
    set @current_row_number = @current_row_number + 1
 
   end
 
   -- display the resultS set with the calculated values
   -- on a daily basis
   select 
    date
   ,symbol
   ,[close]
   ,@period [period length]
   ,ema ema
   from #temp_for_ema
   where row_number < = @max_row_number
   order by row_number
 
end
go

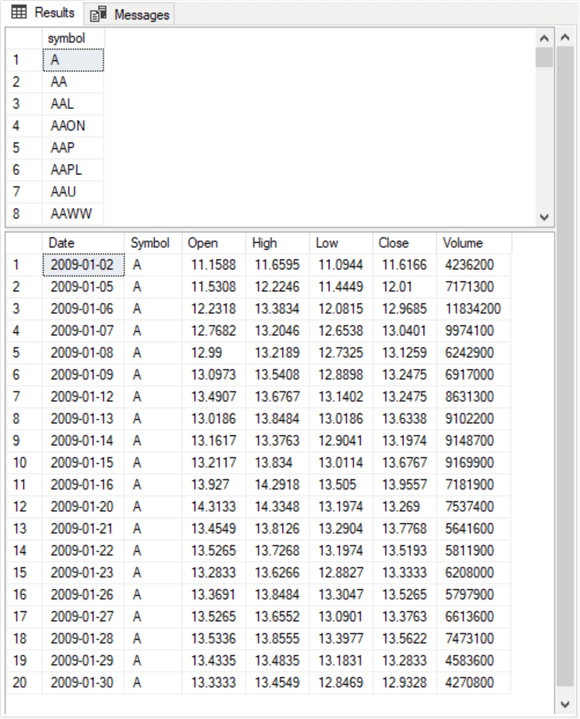
Here’s a screen shot of an exec statement for the usp_ema_computer stored procedure and the results set generated by the final select statement in the stored procedure. The exec statement passes three parameters to the stored procedure.

• The first parameter is for a stock symbol named A.
• The second and third parameters are, respectively, the period length and α values for the exponential moving averages.
• The results set in the screen shot matches the sample results for the symbol A in the "The equations for computing exponential moving averages" section.

Saving exponential moving averages from usp_ema_computer

One main reason for computing exponential moving averages is to save them for easy re-use. This section illustrates one approach to saving exponential moving averages.

• The section starts by creating a table for storing a set of seven exponential moving averages – each one with a different period length.
• Next, the exponential moving averages are computed using the usp_ema_computer stored proc from the preceding section.
  • Each of the seven distinct sets of moving averages is stored in a table without any indexes or keys.
  • Recall that exponential moving averages are defined for an entity, such as a ticker symbol.
  • Any time series value can have one or more matching exponential moving averages – each of which is defined by a unique period length.
  • This tip demonstrates the creating and saving of exponential moving averages with seven different period lengths. These period length values are: three, eight, ten, twenty, thirty, fifty, and two-hundred. However, there is nothing about the approach illustrated in this tip that restricts you to these seven period lengths. Feel free to adapt the approach for any set of period lengths that your applications may require.
  • By using a table without any indexes or keys for saving moving averages, you can cut the time to save the moving averages. This is especially critical when working with thousands of entities and multiple period lengths. After the table is loaded for all entities, you can add one or more indexes to the table. These indexes can help you to extract subsets of values from the full set of exponential moving averages for all dates, entities, and period lengths. This section closes by adding a primary key constraint to the unindexed table for storing exponential moving averages.

The following script demonstrates how to store exponential moving averages and add an index that can expedite data retrieval for subsets of stored moving averages.

• After the use statement, a begin…catch construction drops any prior version of the date_symbol_close_period_length_ema table.
• Next, a fresh copy of the date_symbol_close_period_length_ema table is created.
  • The period length and symbol columns mark the ema column values as belonging to one of a set of moving averages.
  • The date and close column values identify time series values within each symbol.
  • The ema column values are the exponential weighted averages for the close values across dates within symbols and period lengths.
• After the table is created, a fresh copy of a stored procedure is created for populating the table with exponential moving averages.
  • The stored procedure’s name is insert_computed_emas.
  • This stored procedure has one input parameter named @symbol. The stored procedure’s job is to compute seven sets of exponential moving averages for the symbol name in the @symbol parameter.
  • After the as keyword, there are seven pairs of insert into and exec statements. Each pair is to populate the date_symbol_close_period_length_ema table with one of seven sets of exponential moving averages. The insert into statement readies SQL Server to populate the table with the exponential moving average values created by running usp_ema_computer with an exec statement. The three parameters at the end of each exec statement are respectively for the symbol name, period length, and α value for computing a set of exponential moving averages.
• The next four exec statements successively invoke the insert_computed_emas stored procedure four times – once for each of the four symbols in this demonstration. These statements add freshly computed exponential moving averages to the date_symbol_close_period_length_ema table.
• The remainder of the stored procedure illustrates an optional feature of the approach – namely, how to drop and create a fresh version of a primary key for the date_symbol_close_period_length_ema table based on the symbol, date, and period length columns.

-- demo computing and saving emas
 
use [for_csv_from_python]
go
 
-- create a fresh copy of a table to store
-- underlying values and moving averages with different period lengths
begin try
   drop table [dbo].[date_symbol_close_period_length_ema]
end try
begin catch
   print '[dbo].[date_symbol_close_period_length_ema] is not available to drop'
end catch
 
create table [dbo].[date_symbol_close_period_length_ema](
   [date] [date] NOT NULL,
   [symbol] [nvarchar](10) NOT NULL,
   [close] [money] NULL,
   [period length] [float] NOT NULL,
   [ema] [money] NULL
)
go
 
 
declare @symbol nvarchar(10)
 
 
-- conditionally drop a stored proc to save emas
if object_id('dbo.insert_computed_emas') is not null 
     drop proc dbo.insert_computed_emas
go
 
-- create stored proc to save emas
create procedure dbo.insert_computed_emas
   -- Add the parameters for the stored procedure here
    @symbol nvarchar(10)  -- for example, assign as 'GOLD'
 
as
   -- compute and insert emas for @symbol value for 7 different period lengths
   insert into [dbo].[date_symbol_close_period_length_ema]
   exec usp_ema_computer @symbol, 3, 0.500000000000000
 
   insert into [dbo].[date_symbol_close_period_length_ema]
   exec usp_ema_computer @symbol, 8, 0.222222222222222
 
   insert into [dbo].[date_symbol_close_period_length_ema]
   exec usp_ema_computer @symbol, 10, 0.181818181818182
 
   insert into [dbo].[date_symbol_close_period_length_ema]
   exec usp_ema_computer @symbol, 20, 0.095238095238095
 
   insert into [dbo].[date_symbol_close_period_length_ema]
   exec usp_ema_computer @symbol, 30, 0.064516129032258
 
   insert into [dbo].[date_symbol_close_period_length_ema]
   exec usp_ema_computer @symbol, 50, 0.039215686274510
 
   insert into [dbo].[date_symbol_close_period_length_ema]
   exec usp_ema_computer @symbol, 200, 0.009950248756219
 
go
 
-- run stored proc to save computed emas
exec dbo.insert_computed_emas 'ACAD'
exec dbo.insert_computed_emas 'CROX'
exec dbo.insert_computed_emas 'FFIV'
exec dbo.insert_computed_emas 'GOLD'		

-- drop any prior primary key constraint named symbol_date_period_length 
-- not required if fresh version of date_symbol_close_period_length_ema table 
-- is created before populating the table 
begin try 
alter table [dbo].[date_symbol_close_period_length_ema] 
drop constraint [symbol_date_period_length] 
end try 
begin catch 
print 'primary key not available to drop' 
end catch 

-- add a constraint to facilitate retrieving saved emas 
alter table [dbo].[date_symbol_close_period_length_ema] 
add constraint symbol_date_period_length 
primary key (symbol, date, [period length]); 

Retrieving exponential moving values from the date_symbol_close_period_length_ema table

The exponential moving averages saved in the preceding section are stored in a normal form layout. Each row contains a single moving average along with identifiers to describe the moving average values. Also, each row contains a close price value which is the value being averaged via the exponential smoothing expressions.

Here’s a short script to list the first 28 rows from the date_symbol_close_period_length table where the exponential moving values are stored.

• The use statement sets the default database context.
• The asterisk in the select statement causes all the column values from the source data table to appear
• The top keyword phrase before the asterisk restricts the results set to the first twenty-eight rows from the source data table.

use for_csv_from_python
go
 
-- the ema values are saved in normal form
-- by period length, within date, within symbol 
select top 28 * 
from [dbo].[date_symbol_close_period_length_ema] 

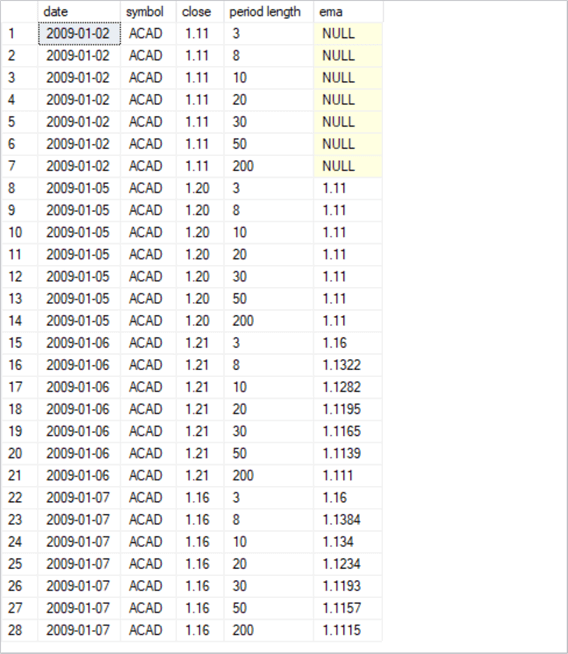
Here’s what the results set from the preceding script looks like.

• Notice that each date value repeats seven times starting with the first date (2009-01-02) from the time series data source.
• All column values for symbol are ACAD because the first twenty rows are all for this stock symbol. Recall that the first primary key column value for the table of moving averages is symbol.
• Close column values repeat in sets of seven. There are four sets of seven close prices.
• The period length column values also repeat, but the arrangement of sets is different than for the other columns. The seven distinct period lengths each appear once per distinct date column value. The period_length field nests within date for the primary key constraint.
• The ema column displays the saved exponential moving averages. Notice the first seven values are NULL because there is no exponential moving average defined for the first date in a time series.

In general, you will not want to display exponential moving averages this way although it is the most straightforward way to list exponential moving averages alongside time series values. One type of request you might get is to list the exponentially smoothed close price values for a specific period length. The following script and the results set below it is one way to respond to this type of request.

• The script uses the @symbol local variable to specify a stock symbol for which to return results.
• The select statement list starts with a top keyword phrase to restrict the output to the first twenty-eight rows.
• The where clause in the select statement specifies two criteria: one for the symbol about which to report exponential moving averages and a second to designate the period length for which to report moving averages.

-- However, you can de-normalize the ema values 
-- and show ema values for one period length for any symbol across dates

declare @symbol nvarchar(10) = 'FFIV'
 
select top 28 date, symbol, [close], ema ema_10
from [dbo].[date_symbol_close_period_length_ema] 
where symbol = @symbol and [period length] = 10

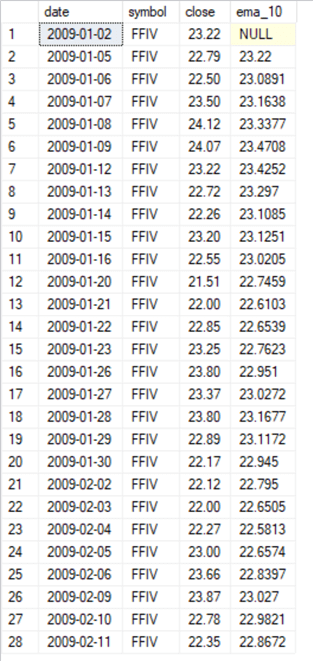
Just as you can display the exponential moving averages for one period length, you can also concurrently show moving averages with multiple period lengths. The following script shows how to list moving averages with period lengths of ten, thirty, fifty, and two hundred. All the moving averages are for a stock symbol of GOLD.

• Again, a declare statement with a local variable specifies the symbol for which to return results.
• An outer query statement inner joins four separate select statements.
  • Each inner select statement contains all columns for a single period length’s results, but the inner queries have different results for just one column – the ema column.
  • The select statement for each inner query is different in three ways.
    • First and most importantly, a where clause criterion designates a different period length – either ten, thirty, fifty, or two hundred.
    • Second, the ema column is aliased as either ema_10, ema_30, ema_50, or ema_200.
    • Third, the inner queries have distinct names based on the period name for which they extract values from symbol_10 for the select statement extracting ten-period length exponential moving averages through symbol symbol_200 for the select statement extracting the two-hundred period length exponential moving averages.
  • The outer select statement references the names from the inner queries to
    • Extract all columns from the symbol_10 query
    • Extract just the ema column name from the symbol_30, symbol_50, and symbol_200 queries.

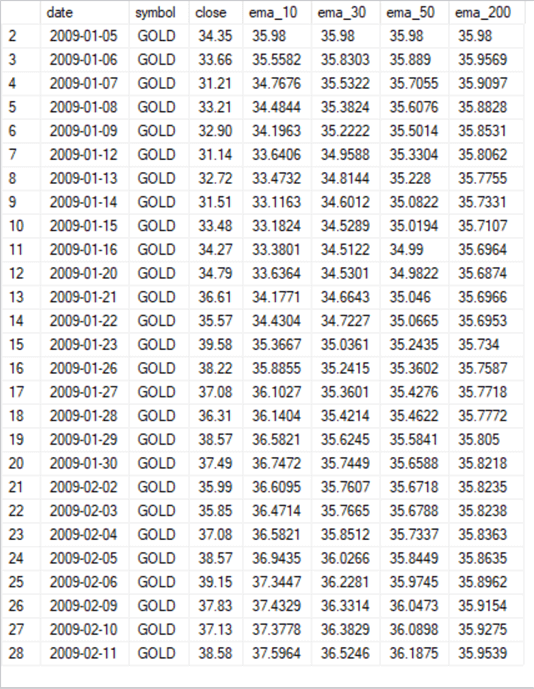
-- or any set of period lengths for any symbol across dates
 
declare @symbol nvarchar(10) = 'GOLD'
 
-- extract and join one column at a time for ema for GOLD symbol
select top 28 symbol_10.*, symbol_30.ema_30, symbol_50.ema_50, symbol_200.ema_200
from
(
   select date, symbol, [close], ema ema_10
   from [dbo].[date_symbol_close_period_length_ema] 
   where symbol = @symbol and [period length] = 10
) symbol_10
 
inner join
 
(
   select date, symbol, [close], ema ema_30
   from [dbo].[date_symbol_close_period_length_ema] 
   where symbol = @symbol and [period length] = 30
) symbol_30
 
on symbol_10.DATE = symbol_30.DATE
 
inner join
 
(
   select date, symbol, [close], ema ema_50
   from [dbo].[date_symbol_close_period_length_ema] 
   where symbol = @symbol and [period length] = 50
) symbol_50
 
on symbol_10.DATE = symbol_50.DATE
 
inner join
 
(
   select date, symbol, [close], ema ema_200
   from [dbo].[date_symbol_close_period_length_ema] 
   where symbol = @symbol and [period length] = 200
) symbol_200
 
on symbol_10.DATE = symbol_200.DATE

Here’s what the results from the prior script looks like.

• The date, symbol, close, and ema_10 columns are from the symbol_10 sub-query.
• The ema_30, ema_50, and ema_200 columns are, respectively, from symbol_30, symbol_50, and symbol_200 sub-queries.

Next Steps

Try out the code examples for this tip with the sample code and data from this tip’s download file. Also, apply the code to your own time series data.

The T-SQL scripts displayed within this tip are available from the tip’s download file. The download file also contains two Excel spreadsheet files -- one for computed exponential moving averages displayed in the "The equations for computing exponential moving averages" section and the other for the time series data for the five symbols referenced by code samples within this tip (A, ACAD, CROX, FFIV, GOLD).

To run the code exactly as described in this tip load on your database server the time series values into a table named (yahoo_prices_valid_vols_only) within the dbo schema of a database named for_csv_from_python. The original size of the fact table in the for_csv_from_python is too large to support a quick download from this tip. However, the code for a re-creation of the full database is provided in this tip and this tip.

About the author

Rick Dobson is an author and an individual trader. He is also a SQL Server professional with decades of T-SQL experience that includes authoring books, running a national seminar practice, working for businesses on finance and healthcare development projects, and serving as a regular contributor to MSSQLTips.com. He has been growing his Python skills for more than the past half decade -- especially for data visualization and ETL tasks with JSON and CSV files. His most recent professional passions include financial time series data and analyses, AI models, and statistics. He believes the proper application of these skills can help traders and investors to make more profitable decisions.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips