Avoiding erroneous results when using T-SQL Trigonometric Functions in SQL Server 2012

By: Dallas Snider | Comments (3) | Related: > TSQL

Problem

One needs to be careful when using the T-SQL trigonometric functions in SQL Server to prevent erroneous output. The results may not always be what they should be. Read this tip and review the examples to learn why.

Solution

In this tip we will start with what works and then we will review the pitfalls that one might encounter when using SQL Server T-SQL trigonometric functions. All examples shown will use the cosine function and use values in both degrees and radians. These first two queries return the correct values for cosine.

select round(cos(0*pi()/180.0),3) as cosineOf0, 
round(cos(90.0*pi()/180.0),3)  as cosineOf90,  
round(cos(180.0*pi()/180.0),3) as cosineOf180, 
round(cos(270.0*pi()/180.0),3) as cosineOf270, 
round(cos(360.0*pi()/180.0),3) as cosineOf360
select round(cos(radians(0.0)),3) as cosineOf0, 
round(cos(radians(90.0)),3)  as cosineOf90,  
round(cos(radians(180.0)),3) as cosineOf180, 
round(cos(radians(270.0)),3) as cosineOf270, 
round(cos(radians(360.0)),3) as cosineOf360

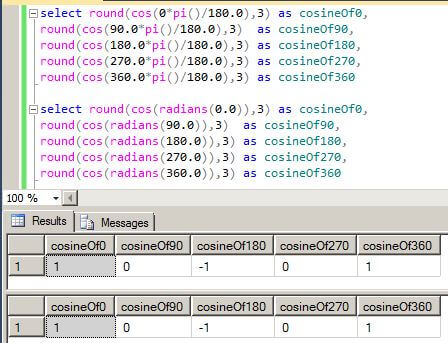
Avoiding Errors when Using T-SQL Trigonometric Functions in SQL Server 2012

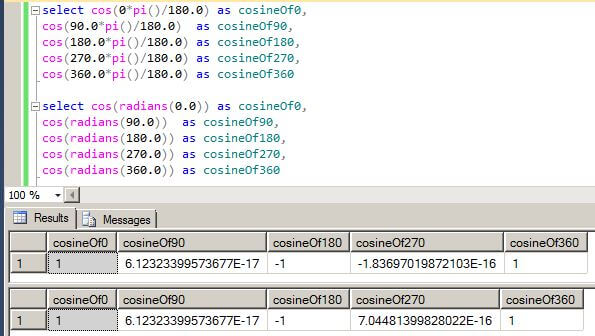
The next two queries demonstrate what happens if you do not round your results. The results for the angle at pi*n radians is correct, but the results at pi*n/2 radians are not correct. The values approach zero, but never equal zero.

select cos(0*pi()/180.0) as cosineOf0, 
cos(90.0*pi()/180.0)  as cosineOf90, 
cos(180.0*pi()/180.0) as cosineOf180, 
cos(270.0*pi()/180.0) as cosineOf270, 
cos(360.0*pi()/180.0) as cosineOf360
select cos(radians(0.0)) as cosineOf0, 
cos(radians(90.0))  as cosineOf90, 
cos(radians(180.0)) as cosineOf180, 
cos(radians(270.0)) as cosineOf270, 
cos(radians(360.0)) as cosineOf360

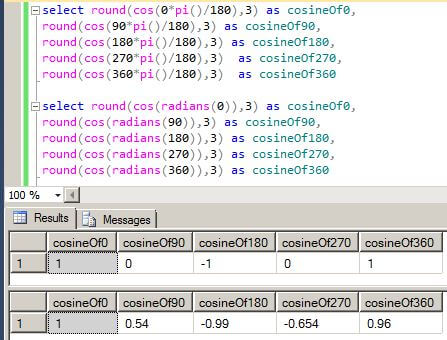
The next two queries show what happens when you use integers for the value of the angle in degrees. The conversion from degrees to radians in the first query below is successful, but in the second query the results are not correct.

select round(cos(0*pi()/180),3) as cosineOf0, 
round(cos(90*pi()/180),3) as cosineOf90, 
round(cos(180*pi()/180),3) as cosineOf180, 
round(cos(270*pi()/180),3)  as cosineOf270,
round(cos(360*pi()/180),3)  as cosineOf360
select round(cos(radians(0)),3) as cosineOf0, 
round(cos(radians(90)),3) as cosineOf90, 
round(cos(radians(180)),3) as cosineOf180, 
round(cos(radians(270)),3) as cosineOf270,
round(cos(radians(360)),3) as cosineOf360

If we look closely at the radians function in the next two queries, we can find the source of the error.

select radians(0.0) as Radians0, 
radians(90.0) as Radians90, 
radians(180.0) as Radians180, 
radians(270.0) as Radians270, 
radians(360.0) as Radians360
select radians(0) as Radians0, 
radians(90) as Radians90, 
radians(180) as Radians180, 
radians(270) as Radians270, 
radians(360) as Radians360

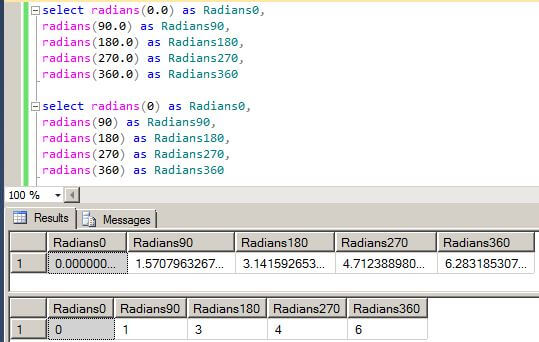
When passing an integer to the radians function, the results returned are an integer which is the floor (rounded down) value. When passing a floating point value to the radians function, the results returned are the correct floating point value.

Next Steps

When using trigonometric functions in T-SQL, make sure to test for cases where the angle is at 0, 90, 180, 270 and 360 degrees. This is the same as 0, pi/2, pi, 3*pi/2 and 2*pi radians.
Check out these tips on other T-SQL functions on MSSQLTips.com.

About the author

Dr. Dallas Snider is an Assistant Professor in the Computer Science Department at the University of West Florida and has 18+ years of SQL experience.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips

Comments For This Article

Tuesday, April 29, 2014 - 5:04:25 PM - Amos

Hello

As an addition to the great article, it is important how we write the explicit conversion to radians.

If we write the following query:

select sin((30/180)*pi()) as sinus_of_30,

cos((30/180)*pi()) as cosinus_of_30,

tan((30/180)*pi()) as tangens_of_30

We'll get the the wrong values 0,1,0 respectively, which are not the sine, cosine and

tangens of 30 degrees.

If we add to the query the following line:

cot((30/180)*pi()) as cotangens_of_30

We'll get an error.

The reason of it is as follows:

If we divide an integer number bu an othe integer one, the result is the integer

value of the division. For example 7/3 yields 2 and not 2 and 1/3.

In the example above we cakculate 30/180 rgar yields 0 and actually we

compute the sine, cosine and tangens of 0. Since a cotangens of an angle

equals 1 divided by its tangend, we get a division by zero.

Therefore we have to add a decimal point near the angle near 180 or near both of

them. Now the predominant type in the division operation is float and therefore the

result is float. Afterthat multiplying it nby pi()

- a float value yields a float result

Now the query

select sin((30./180)*pi()) as sinus_of_30,

cos((30./180)*pi()) as cosinus_of_30,

tan((30./180)*pi()) as tangens_of_30,

cot((30./180)*pi()) as cotangens_of_30

yields correct values

In the artivle the line

select sin(30*pi()/180)as sinus_of_30

yields the same correct result as:

select sin(30.*pi()/180) as sinus_of_30

Why?

The predominant type in the product: 30*pi()

is float(The result of the function pi() is float)

and the division of this float value by 180 yields

a flaot value too. Thefore the calculated sine value is correct.

Thank you

Friday, February 28, 2014 - 9:30:48 AM - jhogue

Great article.

But ...

A fundamental question - maybe this will mark me as a noob -

While I understand that complex mathematical functions such as standard deviation should have a place in T-SQL, err what are trigonometric functions in there in the first place ?

Thursday, February 27, 2014 - 10:21:44 AM - ACOSErrors	Back To Top (29600)
Much more concerning that floating point values not equalling integer values, which is normal, is that some of the trig functions end up rounding their floating point output above the possible inputs for other trig functions. For instance, in a radius search, certain input values can lead to ACOS() throwing an error because the input is over 1.