Implementing Luhn's Algorithm in T-SQL to validate credit card numbers

By:   |   Comments (16)   |   Related: > Functions User Defined UDF


Problem

You are tasked with checking account or credit card numbers for validity, for example as part of a web application handling sensitive card data. You wish to implement this as a function within SQL Server, with the ability to be called with any number and return either TRUE (valid) or FALSE (invalid). Alternatively, you are looking for a method to validate a number based on a check digit: you could be using this as part of a password reset check, for account verification or similar purposes.

Solution

The industry standard for checking credit card numbers for validity is known in colloquial terms as the 'MOD 10 Check', or more formally as Luhn's Algorithm. It has no cryptographic validity, but it is a useful rule-of-thumb check that can be used to validate that a card number is correct, and can be used in its opposite form to generate account (and credit card) numbers - to help discourage potential fraudsters, this function is NOT covered here.

Much literature already exists on Luhn's Algorithm, links for which are provided in the Next Steps section at the end of this tip. The algorithm is simple, but powerful. In the following sections I will provide a step-by-step guide to validating these numbers by hand, then show how we can replicate this as a User-Defined Function (UDF) within SQL Server. I will also show you a method to remove 'noise' from the number - for example, spaces or leading/trailing characters.

One final note - any card numbers used here for illustration / example are fictitious - these pass the MOD 10 check, but are not real credit card numbers, only samples. The samples are from PayPal and may be found here: www.paypalobjects.com/en_US/vhelp/paypalmanager_help/credit_card_numbers.htm

Algorithm Overview

The algorithm can be broken down into 4 stages. All stages are carried out using simple mathematics and rules.

Stage 1: N * 2 for every 2nd N from the right

Let's first get a number which we are testing for validity and split it out into its component digits, in a format we can easily understand. The number we will use is an AMEX sample card number:

Implementing Luhn's Algorithm in T-SQL

The first step is to apply N*2 to every 2nd digit starting from the right. This is true regardless of the length of the number (odd or even number of digits), and is because the final digit is normally a check digit. Let's do this now.

N * 2 for every 2nd N from the right

Stage 2: If (N*2) > 9 sum the digits, else carry the digits

In this stage, we carry forward ALL the digits from either the original number or N*2 to produce a final number for verification. The rule is: If the number was doubled in Stage 1 AND this number > 9, then sum the digits. So if the original number was 9, for example, and was selected for doubling in Stage 1 to become 18, we now need to add 1 + 8 = 9 since 18 > 9. Likewise, if the number 2 was doubled in Stage 1 to equal 4, because 4 < 9 we do not need to transform it further. All other digits - i.e. those NOT selected in Stage 1 - are carried forward without transformation.

This is easier to show than describe. Like so:

If (N*2) > 9 sum the digits, else carry the digits

So now we have a final number that we can check for validity.

Stage 3: Sum the digits

This stage is simple - take this output number and sum the digits.

This stage is simple - take this output number and sum the digits.

This results in a single output integer we'll call X, in this case 80. We now need to test this number - more formally, IF X % 10 = 0 THEN TRUE ELSE FALSE. For those of you unfamiliar with the MOD operation, it's almost interchangeable with the term 'is divisible by'. When we MOD two numbers, we fetch the remainder of the division operation between the two numbers. So, 10 MOD 2 = 0 because 2 evenly divides into 10 with no remainder. 250 MOD 30 = 10, because 250 is divisible by 30 a total of 8 times (240) with 10 remainder. In SQL and in mathematics, MOD is represented by the percentage (%) sign.

Stage 4: IF X MOD 10 = 0 THEN TRUE ELSE FALSE

Applying this then, we know that 80 MOD 10 = 0, therefore the card number is valid.

Applying this then, we know that 80 MOD 10 = 0, therefore the card number is valid.

For balance, let's show the same grid, but this time using an invalid card number. You can see the algorithm quickly generates an output X that fails the MOD 10 check.

You can see the algorithm quickly generates an output X that fails the MOD 10 check.

Rewriting this for SQL Server

Let's now turn our attention to rewriting this in T-SQL.

The code we write must be fairly efficient, but we're constrained in a unique way by using T-SQL - we're writing in the language of relational set theory, not in object oriented language. So whereas in Python or C we might implement the card number as an array of numbers then apply transformations to all elements of the array, we don't have that luxury in SQL Server. What we CAN do, however, is use a temporary table variable to the same effect.

We must also cleanse the card number and make sure we don't have any trailing spaces. In the real world, we'll receive a number for testing as a string, or VARCHAR of indeterminate length, so we'll work on this basis rather than using an INT/BIGINT.

Luckily we can combine this and use a temporary table variable both for cleansing the number and for validity checking.

Let's now set up the function header, and put in a couple of simple constraints - the function can accept a string no longer than 20 characters, and if there aren't at least three digits present in the string, return an error code:

CREATE FUNCTION dbo.usp_LuhnsAlgorithm_New ( @inputString VARCHAR(20) )
RETURNS TINYINT 
AS BEGIN 
-------------------------------------------------------------------------------
-- Function to calculate whether a number is valid according to the 'MOD 10'
-- check, a.k.a. Luhn's Algorithm.
-- Author:  Derek Colley, August 2014
-- Parameters:  @inputString VARCHAR(20) 
-- Outputs:  TINYINT:    2 = an error occurred, validity undetermined
--       0 = number is not valid 
--       1 = number is valid
-------------------------------------------------------------------------------

-- first a quick check to ensure we have at least 3 numbers in the string - 
-- you can change this to any arbitrary amount, i.e. if you are just 
-- checking credit card numbers, make it 13 digits

DECLARE @result TINYINT

IF @inputString NOT LIKE ('%[0-9]%[0-9]%[0-9]%') 
 RETURN 2

Now, we're going to use a table variable to handle the calculation.

-- set up our table for algorithm calculation

DECLARE @charTable TABLE ( 
 Position INT NOT NULL, 
 ThisChar CHAR(1) NOT NULL, 
 Doubled TINYINT, 
 Summed TINYINT )

There's a neat trick we can use now. The instinctive approach to parsing this string is to step through it one character at a time, removing whitespace and non-numeric data. However, we're in a set-based environment. Neither do we want to encapsulate the string in many string-parsing functions like SUBSTRING, REPLACE, CHARINDEX and the like, as this will get very messy very quickly, and our key tool LIKE isn't rich in functionality compared to the non-database equivalent functions.

For this reason, we'll pivot the string into a table, each row containing one character. Using this methodology, we can quickly eliminate unwanted characters while retaining order, and additionally we can use multiple columns for our calculations.

-- convert the @inputString to a fixed width char datatype 
-- we can then process the string as a set with a known number of elements
-- this avoids RBAR substringing each char to a table in a cursor

SET @inputString = CAST(@inputString AS CHAR(20))
INSERT INTO @charTable(Position, ThisChar) 
 SELECT 1, SUBSTRING(@inputString, 1, 1) UNION ALL 
 SELECT 2, SUBSTRING(@inputString, 2, 1) UNION ALL 
 SELECT 3, SUBSTRING(@inputString, 3, 1) UNION ALL 
 SELECT 4, SUBSTRING(@inputString, 4, 1) UNION ALL 
 SELECT 5, SUBSTRING(@inputString, 5, 1) UNION ALL 
 SELECT 6, SUBSTRING(@inputString, 6, 1) UNION ALL 
 SELECT 7, SUBSTRING(@inputString, 7, 1) UNION ALL 
 SELECT 8, SUBSTRING(@inputString, 8, 1) UNION ALL 
 SELECT 9, SUBSTRING(@inputString, 9, 1) UNION ALL 
 SELECT 10, SUBSTRING(@inputString, 10, 1) UNION ALL 
 SELECT 11, SUBSTRING(@inputString, 11, 1) UNION ALL 
 SELECT 12, SUBSTRING(@inputString, 12, 1) UNION ALL 
 SELECT 13, SUBSTRING(@inputString, 13, 1) UNION ALL 
 SELECT 14, SUBSTRING(@inputString, 14, 1) UNION ALL 
 SELECT 15, SUBSTRING(@inputString, 15, 1) UNION ALL 
 SELECT 16, SUBSTRING(@inputString, 16, 1) UNION ALL 
 SELECT 17, SUBSTRING(@inputString, 17, 1) UNION ALL 
 SELECT 18, SUBSTRING(@inputString, 18, 1) UNION ALL 
 SELECT 19, SUBSTRING(@inputString, 19, 1) UNION ALL 
 SELECT 20, SUBSTRING(@inputString, 20, 1)

We could have also achieved this with a WHILE loop instead, but this way is also valid and a loop hardly seems worthwhile for 20 characters.

So now let's clean up the data.

-- remove non-numerics inc. whitespace from the string 

DELETE FROM @charTable
WHERE  ThisChar NOT LIKE('[0-9]')

As we all know, DELETing from a table with an IDENTITY column doesn't reset the identities in that table to become continuous - we land up with holes in the identity sequence. So, for example, if we had five rows in a table with identities 1-5 and we DELETE the row with identity 4, we don't have a table with identities 1-4 - we have a table with identities 1-3 and 5.

We need to fix this, as we're going to use this measure to work out which rows to calculate upon based on whether they are odd or even. And this opens a real can of worms - my first attempt to do this was met with protests by SQL Server that an UPDATE is side-effecting and not allowed in functions. I came up with this:

-- unfortunately this messes up the Position indicator, 
-- so let's 'reset' this like so... 
DECLARE @tempTable TABLE ( 
 NewPosition INT IDENTITY(1,1), 
 OldPosition INT ) 
INSERT INTO @tempTable (OldPosition)
 SELECT Position 
 FROM @charTable 
 ORDER BY Position ASC 

UPDATE  @charTable
SET   Position = t2.NewPosition 
FROM  @charTable t1 
INNER JOIN  @tempTable t2 ON t1.Position = t2.OldPosition

Bonus Material

If you're interested, here's my original version. It uses a Common Table Expression to expose a rendition of the table with a corrected version of the position, then joins the tables using the original positions.

;WITH Repositioned (NewPosition, OldPosition) AS ( 
      SELECT      ROW_NUMBER() OVER ( ORDER BY Position ) [NewPosition], 
                  Position [OldPosition]
      FROM  @charTable ) 
UPDATE            t1
SET               t1.Position = t2.NewPosition 
FROM        @charTable t1 
INNER JOIN  Repositioned t2 ON t1.Position = t2.OldPosition

Also, in the main code, it's worth noting that in functions you cannot issue a statement that changes the database - a function is designed to return values. This extends to temporary objects too, even though they're allowed. Confused? You'll see that in this segment: 

UPDATE  @charTable
SET   Position = t2.NewPosition 
FROM  @charTable t1 
INNER JOIN  @tempTable t2 ON t1.Position = t2.OldPosition

I have specified to update @charTable rather than the alias t1. UPDATE statements on table variables are allowed in functions, but aliases will fail.

Calculations

Now let's do our calculations.

-- now for every 2nd digit from the right of the numeric, 
-- double it and store the result in the Doubled column 

IF ( SELECT MAX(Position) % 2 FROM @charTable ) = 0 -- evens 
BEGIN 
 UPDATE @charTable
 SET  Doubled = CAST(ThisChar AS TINYINT) * 2 
 WHERE Position % 2 <> 0 
END
ELSE BEGIN -- odds
 UPDATE @charTable 
 SET  Doubled = CAST(ThisChar AS TINYINT) * 2 
 WHERE Position % 2 = 0 
END

We can take advantage of SQL Server's unwillingness to divide two INTs correctly (the result is reported as an INT) to simplify our equation:

-- now if the doubled digit is > 9, sum the digits, else carry forward
-- to the Summed column.  This goes for non-doubled digits too.
UPDATE @charTable
SET  Summed = 
   CASE WHEN Doubled IS NULL 
     THEN CAST(ThisChar AS TINYINT) 
     WHEN Doubled IS NOT NULL AND Doubled <= 9 
     THEN Doubled 
     WHEN Doubled IS NOT NULL AND Doubled >= 10 
     -- sum the digits.  Luckily SQL Server butchers int division...
     THEN (Doubled / 10) + (Doubled - 10) 
   END

And now let's define our validity conditions based on the modulo output.

-- finally, sum the Summed column and if the result % 10 = 0, it's valid 
IF ( SELECT SUM(Summed) % 10 FROM @charTable ) = 0
 SET @result = 1
ELSE 
 SET @result = 0

RETURN @result 

END

Let's take a look at the working table. My code doesn't expose this as there's no need - we're only interested in the output value. But for curiosity:

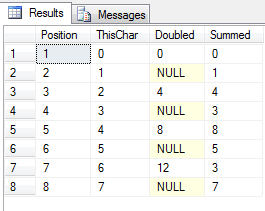
Let's take a look at the working table.

Complete Script

Here is the complete T-SQL code.

CREATE FUNCTION dbo.usp_LuhnsAlgorithm_New ( @inputString VARCHAR(20) )
RETURNS TINYINT 
AS BEGIN 
-------------------------------------------------------------------------------
-- Function to calculate whether a number is valid according to the 'MOD 10'
-- check, a.k.a. Luhn's Algorithm.
-- Author:  Derek Colley, August 2014
-- Parameters:  @inputString VARCHAR(20) 
-- Outputs:  TINYINT:    2 = an error occurred, validity undetermined
--       0 = number is not valid 
--       1 = number is valid
-------------------------------------------------------------------------------

-- first a quick check to ensure we have at least 3 numbers in the string - 
-- you can change this to any arbitrary amount, i.e. if you are just 
-- checking credit card numbers, make it 13 digits

DECLARE @result TINYINT

IF @inputString NOT LIKE ('%[0-9]%[0-9]%[0-9]%') 
 RETURN 2

-- set up our table for algorithm calculation

DECLARE @charTable TABLE ( 
 Position INT NOT NULL, 
 ThisChar CHAR(1) NOT NULL, 
 Doubled TINYINT, 
 Summed TINYINT ) 

-- convert the @inputString to a fixed width char datatype 
-- we can then process the string as a set with a known number of elements
-- this avoids RBAR substringing each char to a table in a cursor

SET @inputString = CAST(@inputString AS CHAR(20))
INSERT INTO @charTable(Position, ThisChar) 
 SELECT 1, SUBSTRING(@inputString, 1, 1) UNION ALL 
 SELECT 2, SUBSTRING(@inputString, 2, 1) UNION ALL 
 SELECT 3, SUBSTRING(@inputString, 3, 1) UNION ALL 
 SELECT 4, SUBSTRING(@inputString, 4, 1) UNION ALL 
 SELECT 5, SUBSTRING(@inputString, 5, 1) UNION ALL 
 SELECT 6, SUBSTRING(@inputString, 6, 1) UNION ALL 
 SELECT 7, SUBSTRING(@inputString, 7, 1) UNION ALL 
 SELECT 8, SUBSTRING(@inputString, 8, 1) UNION ALL 
 SELECT 9, SUBSTRING(@inputString, 9, 1) UNION ALL 
 SELECT 10, SUBSTRING(@inputString, 10, 1) UNION ALL 
 SELECT 11, SUBSTRING(@inputString, 11, 1) UNION ALL 
 SELECT 12, SUBSTRING(@inputString, 12, 1) UNION ALL 
 SELECT 13, SUBSTRING(@inputString, 13, 1) UNION ALL 
 SELECT 14, SUBSTRING(@inputString, 14, 1) UNION ALL 
 SELECT 15, SUBSTRING(@inputString, 15, 1) UNION ALL 
 SELECT 16, SUBSTRING(@inputString, 16, 1) UNION ALL 
 SELECT 17, SUBSTRING(@inputString, 17, 1) UNION ALL 
 SELECT 18, SUBSTRING(@inputString, 18, 1) UNION ALL 
 SELECT 19, SUBSTRING(@inputString, 19, 1) UNION ALL 
 SELECT 20, SUBSTRING(@inputString, 20, 1)


-- remove non-numerics inc. whitespace from the string 
DELETE FROM @charTable
WHERE  ThisChar NOT LIKE('[0-9]') 


-- unfortunately this messes up the Position indicator, 
-- so let's 'reset' this like so... 
DECLARE @tempTable TABLE ( 
 NewPosition INT IDENTITY(1,1), 
 OldPosition INT ) 
INSERT INTO @tempTable (OldPosition)
 SELECT Position 
 FROM @charTable 
 ORDER BY Position ASC 

UPDATE  @charTable
SET   Position = t2.NewPosition 
FROM  @charTable t1 
INNER JOIN  @tempTable t2 ON t1.Position = t2.OldPosition 

-- now for every 2nd digit from the right of the numeric, 
-- double it and store the result in the Doubled column 

IF ( SELECT MAX(Position) % 2 FROM @charTable ) = 0 -- evens 
BEGIN 
 UPDATE @charTable
 SET  Doubled = CAST(ThisChar AS TINYINT) * 2 
 WHERE Position % 2 <> 0 
END
ELSE BEGIN -- odds
 UPDATE @charTable 
 SET  Doubled = CAST(ThisChar AS TINYINT) * 2 
 WHERE Position % 2 = 0 
END 


-- now if the doubled digit is > 9, sum the digits, else carry forward
-- to the Summed column.  This goes for non-doubled digits too.
UPDATE @charTable
SET  Summed = 
   CASE WHEN Doubled IS NULL 
     THEN CAST(ThisChar AS TINYINT) 
     WHEN Doubled IS NOT NULL AND Doubled <= 9 
     THEN Doubled 
     WHEN Doubled IS NOT NULL AND Doubled >= 10 
     -- sum the digits.  Luckily SQL Server butchers int division...
     THEN (Doubled / 10) + (Doubled - 10) 
   END      


-- finally, sum the Summed column and if the result % 10 = 0, it's valid 
IF ( SELECT SUM(Summed) % 10 FROM @charTable ) = 0
 SET @result = 1
ELSE 
 SET @result = 0

RETURN @result 

END

Testing

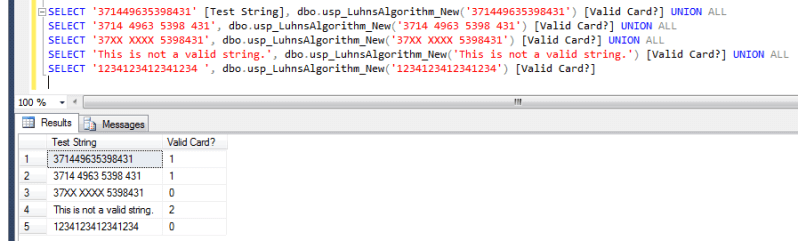
Here is a test script that you can use:

SELECT '371449635398431' [Test String], [dbo].[usp_LuhnsAlgorithm_New]('371449635398431') [Valid Card?] UNION ALL
SELECT '3714 4963 5398 431' [Test String], [dbo].[usp_LuhnsAlgorithm_New]('3714 4963 5398 431') [Valid Card?] UNION ALL
SELECT '37XX XXXX 5398431' [Test String], [dbo].[usp_LuhnsAlgorithm_New]('37XX XXXX 5398431') [Valid Card?] UNION ALL
SELECT 'This is not a valid string' [Test String], [dbo].[usp_LuhnsAlgorithm_New]('This is not a valid string' ) [Valid Card?] UNION ALL
SELECT '1234123412341234' [Test String], [dbo].[usp_LuhnsAlgorithm_New]('1234123412341234') [Valid Card?]

Here's how to call the function, and some test results using one of our sample card numbers discussed earlier and some other input. Recall that output 1 = valid, output 0 = invalid, output 2 = error/bad string:

Recall that output 1 = valid, output 0 = invalid, output 2 = error/bad string
Next Steps


sql server categories

sql server webinars

subscribe to mssqltips

sql server tutorials

sql server white papers

next tip



About the author
MSSQLTips author Derek Colley Derek Colley is a UK-based DBA and BI Developer with more than a decade of experience working with SQL Server, Oracle and MySQL.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips


Comments For This Article




Thursday, March 8, 2018 - 6:34:52 AM - Andy Back To Top (75373)

Hi Derek

Can't thank you enough for this post!

Really gave me a breakthrough with one of the data integrity issues I was struggling with and will put this to good use in the future.

Stlll relvatively new to SQL after many years in MS Access and VBA, but always wanted to take it to te next level.

Your use of this function in a stored procedure has been a big boost to my knowledge (even though I don't yet understand how you did it)

Thank you for sharing this 

Best Regards

 

Andy

 

Wednesday, February 28, 2018 - 9:50:06 AM - Howard C. Shaw III Back To Top (75317)

 

Your calculation of (Doubled/10)+(Doubled-10) seems unnecessary to me. Your case statement, and the fact you are already operating on doubled values of single digits, means your domain is simply (10,12,14,16,18), right? For each of these, Doubled-9 gives the same answer, without the extra division operation:

10-9 = 1

12-9 = 3

14-9 = 5

16-9 = 7

18-9 = 9

Tuesday, January 6, 2015 - 5:08:42 PM - Amos Back To Top (35847)

Hello Derek,

 

   Following my previous post I would to present a shorter code of a user function to check if a credit card

number is llegal/illegal

 

  The stages 1-3 are done in one loop. We're working on the string that represents the credit card number as

an array. We take only the characters that represent digits and we make the calculations on them. We start from

the rightmost digit to the leftmist one. In each loop iteration we multiply the current digit by 1 or 2. The current

multiplier 1 or 2 is calculated by subtracting the previous one  from 3. For example if the previous multiplier is  1,

the current one is 2, because 3-1=2. Another thing, we don't check if multiplying the digit by 2 yields a single

digit/two digits  number. We allways calculate the quotient and the reminder of the division of the product by 10. If we divide

one digit number by 10 - the quotient is 0 and the reminder is the digit itself and the sum is the digit itself.  

 

Hereby a shorter version of  the user defined function:

create function dbo.fn_CheckCreditCardNumber(@inputStr varchar(25))
    returns tinyint
-- parameters: @inputStr  varchar(25)
-- outputs: tinyint: 2 – Credit card number contains
--                       less than 13 digits
--                   0 – Legal credit card number  
--                   1 – Illegal Propre credit card number  
as begin
-- The number of digits of a credit card number must be 13 at least
  if(@inputStr not like ('%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]'))
    return 2

   declare @strLength   smallint,
              @multiplier    tinyint,
              @sum           tinyint,
              @prod           tinyint,
              @i                tinyint,
              @result         tinyint,
             @digit            char(1)

   set @strLength  = len ( @inputStr )
-- Calculating the original number's string length for the loop    control

   set @i          = @strLength

   set @multiplier = 1
   set @sum        = 0


   while(@i >= 1)
   begin
   set @digit = substring(@inputStr, @i, 1)
   if(@digit like '[0-9]')-- A digit
   begin
      set @prod = convert(tinyint , @digit) * @multiplier
      set @sum  = @sum + @prod/10 + @prod % 10 
      set @multiplier = 3 - @multiplier   
   end

      set  @i = @i - 1
   end

-- If the digits' sum modolo 10 equals 0 - divisible
-- without reminder by 10 - the number is legal
   if(@sum %10 = 0)
-- Legal credit card number
     set @result = 1
   else
-- Illegal credit card number
     set @result = 0

   return @result
end

 

Sunday, December 21, 2014 - 12:34:04 AM - Amos Back To Top (35705)

Hello Derek,
     I've seen only now your tip.
 
    As an sql developer, I would like to say rhat it is a nice tip. You are making an efficient use with the
tool that SQL Server gives us - the user defined functions.
 
    You have specified in your article, that in SQL Server we don't have the luxury of
using array to store the digits of the credit card number. What we have to do is using
a temporary table to the same effect.
    I would like to say, that you can use a string in order to simulate an array of digits. You can refer
to each one of its eelements by substring.
   Hereby a function I've written to check ig a check digit is correct. If you've any comments, let me
know:
 
create function dbo.fn_CheckCreditCardNumber(@inputStr varchar(25))
    returns tinyint
-- parameters: @inputStr  varchar(25)
-- outputs: tinyint: 2 – Credit card number contains
--                       less than 13 digits
--                   0 – Legal credit card number  
--                   1 – Illegal Propre credit card number  
as begin
  declare @workStr   varchar(25)
  declare @strLength smallint
  declare @i         smallint
  declare @sum       smallint
  declare @prod      smallint
  declare @digit     char(1)
  declare @evenInd   tinyint
  declare @result    tinyint
-- The number of digits of a credit card number must be 13 at least
  if(@inputStr not like ('%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]%[0-9]'))
 return 2
-- Moving the digits only from the input string to the
-- "digits' array" - A string
-- Calculating the original number's string length for the loop control
   set @strLength = len ( @inputStr )
   set @i = 1
   set  @workStr = ''
   while(@i    begin
  set @digit = substring(@inputStr, @i, 1)
  if(@digit like '[0-9]')-- A digit
-- Adding the digit character to the "digits' array"
  set @workStr = @workStr + @digit
        set @i = @i +1
   end
-- Additional pass on the "digits' array". If the digits number is ---- even, each digit in an odd position is multiplied by 2 and the
-- current position in the array  is changed with the product.
-- Otherwise, each digit in an odd place is multiplied by 2
-- and the current position in the array is change with the product.
-- If the product is more than 9, its digits are sum. The curerent ---- position in the array is changed with this sum.
-- The first, second and the third steps are done in one loop.
    set @sum     = 0
    set @evenInd = 0
    if(@strLength % 2 = 0)
     set @evenInd = 1
    set @i = 1
    while(@i     begin
  set @digit = substring(@workStr, @i, 1)
-- Getting the current digit in the "array"
  set @prod   = convert(smallint , @digit)
  if(@evenInd = 1 and @i % 2 = 1 or
               @evenInd = 0 and @i % 2 = 0)
            set @prod = @prod * 2
  if(@prod >= 10)-- The product by 2 greater than 9
  begin
-- Summing the two digits of the product
   set @prod = @prod/10 + @prod-10
  end
-- Updating the digits' sum
  set @sum = @sum + @prod
  set @i = @i +1
  end
 
-- If the digits' sum modolo 10 equals 0 - divisible
-- without reminder by 10 - the number is proper
  if(@sum %10 = 0)
     set @result = 1 –  Legal credit card number
  else
   set @result = 0 –  Illegal credit card number
  return @result
end
 
Hope to read your opinion

Thank you,
    Amos

   
 
 
    
 

 

Tuesday, September 2, 2014 - 5:12:01 AM - Henn Back To Top (34347)

I have create something similar for checking PIN validation in Excel. Unfortunately this article is only in estonian but the meaning is readable.

at least similar techique works (single formula)

this formula checks cyymmddnnnx 11 number PIN where c is gender+century (1-3-5 male, 2-4-6 female, 1-2 1800, 3-4 1900, 5-6 2000), yy year, mm month, dd day nnn unique number on day and x checksum using standard algorithm

the article is there 

 

https://sarviktaat.wordpress.com/2012/12/06/isikukoodi-valideerimine-excelis/

and the formula is there:

=IF(ISERROR(TEXT((CODE(MID("FEDCA@";LEFT(A11;1);1))-50)*1000000+LEFT(A11;7);"0000\.00\.00")+0);"isikukood vigane";IF(IF(MOD(SUMPRODUCT((MID(A11;COLUMN($A$1:$J$1);1)+0);(MID("1234567891";COLUMN($A$1:$J$1);1)+0));11)=10;MOD(MOD(SUMPRODUCT((MID(A11;COLUMN($A$1:$J$1);1)+0);(MID("3456789123";COLUMN($A$1:$J$1);1)+0));11);10);MOD(SUMPRODUCT((MID(A11;COLUMN($A$1:$J$1);1)+0);(MID("1234567891";COLUMN($A$1:$J$1);1)+0));11))=MID(A11;11;1)+0;"isikukood õige";"kontrolljärk vale"))

"isikukood vigane" means wrong date numbers

"isikukood õige" means everything is valid

"kontrolljärk vale" means checksum isn't valid

 

this isn't actually "SQL Tip" but might be interesting to research :)

Henn

 

Thursday, August 28, 2014 - 11:21:36 AM - Malcolm Back To Top (34321)

Thanks for the updated select statement, I never knew you could do that.

Thursday, August 28, 2014 - 11:10:39 AM - Scott Back To Top (34318)

That is too many steps.  You can condense the whole calculation to one query.

SELECT  @result = 1 - SIGN(SUM(val3) % 10)
FROM (
    SELECT  Position = ROW_NUMBER() OVER (ORDER BY number DESC),
            val1 = CAST(ThisChar AS TINYINT)
    FROM (
        SELECT  number, ThisChar = SUBSTRING(@inputString, number, 1)
        FROM master.dbo.spt_values
        WHERE type = 'P' AND number BETWEEN 1 AND LEN(@inputString)
    ) AllChars
    WHERE ThisChar BETWEEN '0' AND '9'
) Digits
CROSS APPLY ( SELECT val2 = val1 * (2 - Position % 2) ) x
CROSS APPLY ( SELECT val3 = val2 % 10 + val2 / 10 ) y;

Thursday, August 28, 2014 - 6:37:01 AM - Magnus Back To Top (34305) 
SELECT CardNo, [dbo].[usp_LuhnsAlgorithm_New](CardNo) [Valid Card?]  from MyTable


should give you two result columns: the list of card numbers and the result of the function for each card number.

Thursday, August 28, 2014 - 4:30:03 AM - Malcolm Back To Top (34303)

I see how

SELECT [dbo].[usp_LuhnsAlgorithm_New]('37XX XXXX 5398435') [Valid Card?]

would work but haw can you select more than one card number from your table so say something like

SELECT [dbo].[usp_LuhnsAlgorithm_New](select CardNo from MyTable) [Valid Card?]

though I understand that the above does not work, but how can I get the same result?

Thanks

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Wednesday, August 27, 2014 - 2:23:23 PM - Derek Colley Back To Top (34292)
Thanks all for the comments, looks like a popular tip. I agree that generally, good design means credit card numbers shouldn't make it to the DB. For a start, this raises questions about adherence to PCI DSS standards which (in the UK at least) all organisations handling personal data must abide by in some form. However - the tip, as well as being an academic exercise, is also useful for validation in other contexts. Think for example if you wanted to use it to validate an account number, a password verification code, a signature on incoming data, challenge codes ... Also worth noting is that in real life, some companies DO store card details in their databases. In at least two organisations I've worked for, we've had live card data in the DBs by *design* (not mine!). In point of fact, one of my first tasks at my last gig was to write a procedure to scrape the DBs for card data and flag if present for PCI checks. Having this kind of tool in my scripts was very useful for this purpose. Keep up the comments and thanks again!

Wednesday, August 27, 2014 - 2:04:55 PM - m mcdonald Back To Top (34291)

Nice article however, agree with Brent's assertion/concern...

 

Interesting side note:  37XX XXXX 5398435 will test as valid...

Wednesday, August 27, 2014 - 1:23:18 PM - Brent Ozar Back To Top (34288)

Jeremy - you're missing the point. If unencrypted credit card numbers made it into the database layer, then they're a huge security risk. Think Profiler trace or plan cache query.

Wednesday, August 27, 2014 - 11:42:49 AM - Jeremy Kadlec Back To Top (34286)

Thanks everyone for the feedback.  I think the point of this tip was to show how to validate credit numbers with a function, not about storing credit numbers in a SQL Server database.

Thank you,
Jeremy Kadlec
Community Co-Leader

 

Wednesday, August 27, 2014 - 11:25:55 AM - Tibor Nagy Back To Top (34283)

Interesting article but I agree with Brent. You should not have card numbers in your DB. A stored procedure to check the card number when it is entered can be interesting but it is better if the clear card number does not reach the DB.

Wednesday, August 27, 2014 - 8:35:42 AM - Nitin Back To Top (34281)

We only hold the last 4 digits in a DB plus the authorization tocken that was generated when the card was validated.

Having said that I found this article very interesting and will put it into my KB for sure.

Good work.

Wednesday, August 27, 2014 - 8:19:39 AM - Brent Ozar Back To Top (34280)

This is an interesting tip, but I'd zoom out a little and ask, why on earth would you ever want to let unencrypted credit card numbers get into the database layer? That's a huge, huge, HUGE security no-no.














get free sql tips
agree to terms