By: Rick Dobson | Comments | Related: > Functions System
Problem
I seek a starter package for performing statistics with T-SQL. I want a set of stored procedures that is easy to learn and use. Additionally, I want a package that I can enhance on my own for data science requirements that are increasingly being assigned to me.
Solution
A growing number of database professionals are being challenged to analyze the data resources that they manage and maintain. Happily, database professionals can readily gain the skills to meet these challenges. For example, this tip provides a framework for implementing typical statistical techniques in stored procedures. This framework builds on familiar database skills, such as how to write a T-SQL script, transfer a unit-tested script to a stored procedure, create and populate temporary tables, as well as invoke and return data from a stored procedure.
Statistics is often thought of as an esoteric, complicated topic, but this is just not true. Statistics relies on expressions or sometimes even just processes. Statistics are used to address specific tasks, such as identifying the central value from a set of values or telling whether the values in one set is statistically greater than those in another set. To program statistics with T-SQL, all you have to discover is which specific task needs to be performed, find a simple description of how to implement the task, and then code the implementation with T-SQL. Several examples of how to traverse these steps appear inside this tip.
The goal of this tip is to present a suite of stored procedures that implements various statistical techniques with T-SQL. The purpose of each stored procedure is clearly described, and you receive a worked example of how to use each stored procedure. The specific statistical techniques covered in this tip include
- Computing median values for assessing central tendency
- Coefficients of determination for goodness of fit
- Correlation coefficient as well as regression slope and intercept values for describing the fit of a line to some data
- Tests for indicating whether sets of values are statistically different from one another
A framework for the stored procedures in the starter statistics package
Each statistical technique covered in this tip is demonstrated with the help of a stored procedure. However, before writing the stored procedure, I created a script for implementing the statistic computed by the stored procedure. I personally find it easier to debug code in scripts than in stored procedures, but if you find debugging code easier in stored procedures than scripts, then go directly to unit testing in the stored procedure. You may also find it useful to output either from the stored procedure or from code for running a stored procedure supplementary values besides the statistical outcome. Examples of supplementary values that may be useful to output include key input values or intermediate values generated on the way to calculating a statistical outcome.
In any event, you need to write and debug the T-SQL code for whatever statistic your stored procedure aims to compute. I generally seek resources to help me specify the contents of the stored procedure.
- One type of resource conveys the purpose of the statistic along with expressions for computing the statistic.
- The second type of resource includes one or more worked examples that are like the one that I want to implement; this type of resource supports unit testing your code.
Here's some pseudo code that provides a framework for the stored procedures used to compute statistics in this tip.
create procedure stored_procedure_name as begin set nocount on; ------------------------------------------------------------------------------------ Place your debugged code here for a statistic and whatever associated values you want to output from your stored procedure. ------------------------------------------------------------------------------------ return end
I generally populate global temporary tables with sample values for computing the statistic and any associated output from the stored procedure. A global temporary table is convenient because I can debug a script in one SSMS tab and then copy the finished code into another tab from which I am developing the stored procedure for the statistic.
Two stored procedures for computing medians
A median is one of several different statistics for representing the central tendency of a set of values. Other widely known measures of central tendency include the mean and the mode. You can think of the median as a value that separates the upper and lower halves of a sorted set of values. If the number of values in a set is odd, then the median is simply the middle value in the sorted set of values. If the number of values in a set is even, then the median is the average of the last value in the top half and the first value in the bottom half.
As simple as the definition for a median is, the topic has attracted substantial attention from SQL Server developers. Of course, MSSQLTips.com has a prior tip for calculating median values. Additionally, stackoverflow.com offers many different approaches to coding a function to compute a median value. One common reason for the different approaches follows from the evolving features of successive versions of SQL Server. For those using SQL Server 2012 or later, the percentile_cont function is a very appropriate tool for computing a median; this function can serve other purposes as well.
The stored procedure approach to computing medians in this tip relies on the percentile_cont function in two specific contexts.
- First, you'll learn how to compute the median for an overall set of values.
- Second, you'll learn how to compute the median for each category in a set of values where any one category can have one or more values associated with it, but each individual value belongs to just one category.
This tip draws on a prior tip that used medians to designate a central values for sets of values from a process coded in T-SQL. Using an adaptation of key code from the prior tip conveys a feel for how to integrate a stored procedure for computing medians into a custom T-SQL application.
The percentile_cont function calculates the value in a set of values corresponding to a specific percentile value. The syntax for the function from the Microsoft.com site appears below.
- The numeric_literal designates a percentile value. For example, .5 denotes the median value, and .75 points to the 75th percentile.
- The order_by_expression designates the set of values for which the median is being calculated.
- The partition_by_clause term represents the groupings for which to compute medians within a set of values. You can think of partition_by_clause values as category values.
- If the partition_by_clause value is the same for all rows in the source data, then the function returns the overall median.
- If there are multiple partition_by_clause values for several different categories within the source data, then the function returns the median value for each set of order_by_expression values associated with a partition_by_clause value.
- The data_source designator can be any row source, such as a database table or a result set from a select statement.
PERCENTILE_CONT (numeric_literal)
WITHIN GROUP (ORDER BY order_by_expression [ ASC | DESC ] )
OVER ( [ ] )
FROM data_source
The following select statement extracts data from a custom T-SQL application described in a prior tip. The prior tip assesses the price change from buying stocks at a golden cross price and selling them at a death cross price; the tip illustrates how to calculate and use golden/death cross pairs to estimate potentially profitable buy and sell prices for a stock.
- The data source within this tip is a global temporary table named ##table_for_overall_median.
- The query extracts all the columns from the source table with the * term in the select list.
- An additional column named category_value is added. The value of this column for all rows in the result set is set to a literal value of 'overall'.
- The code for deriving the ##table_for_overall_median table and other code in this section is available from the 'script for median overall and by category variable.sql' file that are among the files you can download with this tip.
select *, 'overall' category_value from ##table_for_overall_median
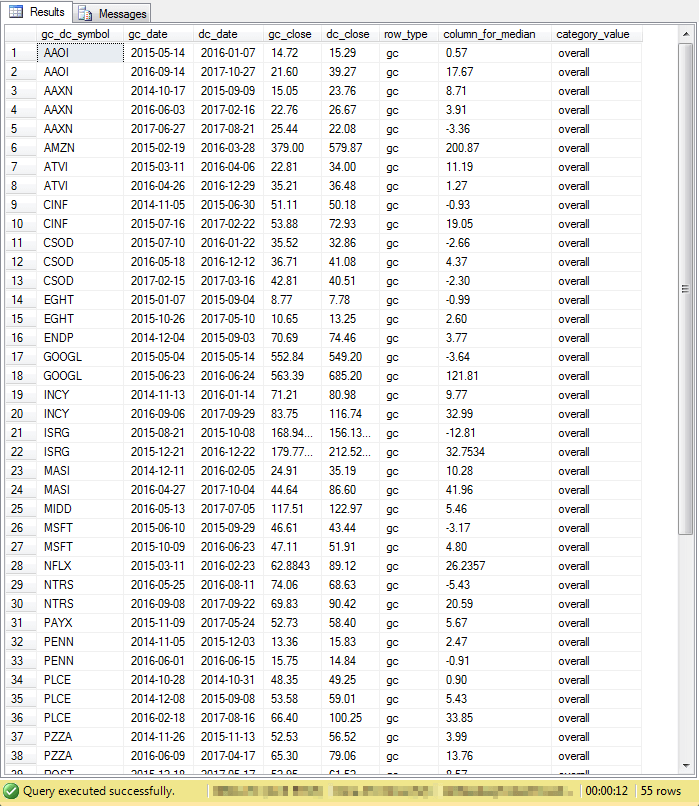
The following screen shot displays an excerpt from the result set for the preceding select statement. As you can see from the lower border, there are 55 rows in the result set.
- Each row is identified by gc_dc_symbol value as well as a pair of dates (gc_date and dc_date).
- The gc_date designates the golden cross date that indicates a potentially good date to buy a stock.
- The dc_date designates the death cross date that indicates a date to sell a stock if it has not been sold previously.
- The values in column_for_median are the change in close price (dc_close - gc_close) from the golden cross date through the death cross date.
- The category_value column is always set to 'overall'.
The next script calculates the overall median value for values in the column_for_median column from the preceding select statement's result set. Notice that the code inside the compute_overall_median stored procedure uses two columns from the ##table_for_overall_median global temporary table. Therefore, you can apply this stored procedure to any set of values for computing an overall median by populating the global temporary table from whatever data source has values requiring a median.
- Assign a column from a table or result set with a set of values for which you require a median to the column_for_median column.
- So long as you are computing a median over all values in the column_for_median column, the category_value for each row should be 'overall'.
create procedure compute_overall_median
as
begin
set nocount on;
-- distinct in select statement shows just one overall median row value
select
distinct percentile_cont(.5)
within group (order by column_for_median)
over(partition by category_value) median_gc_dc_change
from
(
select
*
,'overall' category_value
from ##table_for_overall_median
) for_median
return
end
The following script performs two sets of functions. First, it runs the stored procedure to calculate the overall median for a set of values, saves the median in a table variable (@tmpTable), and then displays the median from the table variable. Second, it displays the source data in a different sort order than the preceding screen shot. This new sort order facilitates the verification of the computed median value.
-- invoke compute_overall_median stored procedure -- display median as median_value from @tmpTable declare @tmpTable table (median_value real) insert into @tmpTable exec dbo.compute_overall_median select * from @tmpTable -- display input to unit test median value computation select * from ##table_for_overall_median order by column_for_median desc
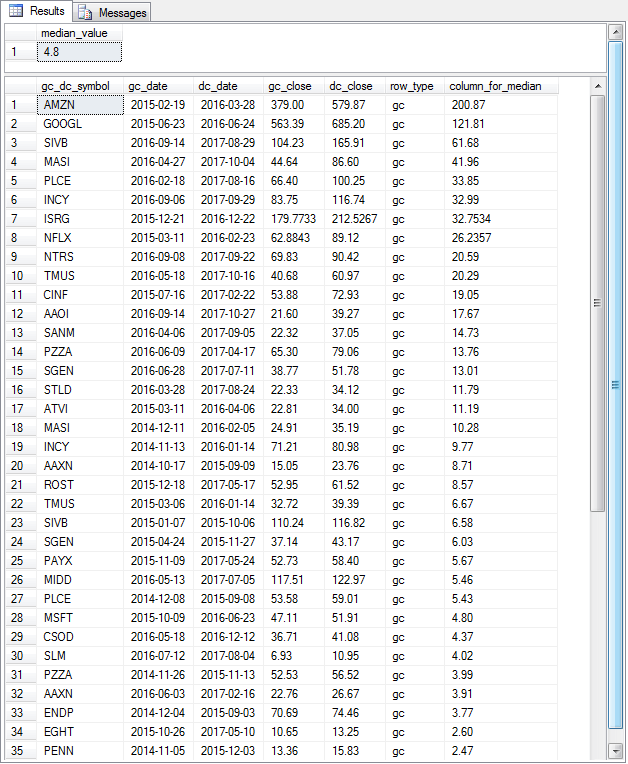
The next screen shot displays the Results tab from the preceding script. There are two panes in the tab.
- The top pane shows the median value - namely 4.8.
- The bottom pane shows the first thirty-five rows of the ##table_for_overall_median global temporary table ordered by column_for_median values in descending order. Notice that value of the twenty-eighth row in the column_for_median column is 4.80. The twenty-eighth row is in the middle of the result set because there are twenty-seven rows above and below it. Recall that the result set has fifty-five rows.
- This outcome confirms that the compute_overall_median stored procedure correctly computes the overall median value for the column_for_median values.
The next script shows the create stored procedure statement to calculate the median change in close price across all the rows for each gc_dc_symbol value in the ##table_for_overall_median global temporary table. For this set of data, symbols occur once, twice or three times. However, the percentile_cont function correctly derives the median change in close price no matter how many rows exist for a symbol.
- The over clause in the percentile_cont function implicitly groups the rows by category value (gc_dc_symbol value) from the result set derived from the ##table_for_overall_median global temporary table.
- The distinct keyword in the select statement containing the percentile_cont function returns just one median value for each symbol no matter how many rows in the ##table_for_overall_median table exist for each symbol.
create procedure compute_median_by_category
as
begin
set nocount on;
select
*
from
(
-- compute median by gc_dc_symbol
-- distinct in select statement shows just one median per symbol
select
distinct category
,percentile_cont(.5)
within group (order by column_for_median)
over(partition by category) median_by_category
from
(
select
category
,column_for_median
from ##table_for_median_by_category
) for_median_by_category
) for_median_by_category
order by category
return
end
The next script excerpt shows the code for invoking the compute_median_by_category stored procedure. As you can see the calculated median values are stored in the @tmpTable table variable and then displayed via a select statement. Next, a select statement displays the source data for the median values from the ##table_for_overall_median table sorted by category value (gc_dc_symbol) and column_for_median value.
-- invoke compute_median_by_category stored procedure -- display category and median_by_category from @tmpTable declare @tmpTable TABLE (category varchar(5), median_by_category real) insert into @tmpTable exec compute_median_by_category select * from @tmpTable -- display input to verify median value select category, column_for_median from ##table_for_median_by_category order by category, column_for_median
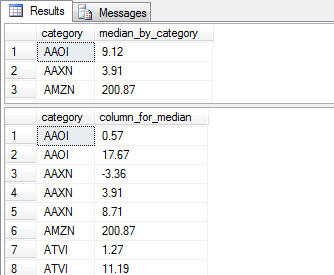
The following screen shot presents excerpts from the two result sets so that you can verify the operation of the code. The top pane shows the calculated median for symbols, and the bottom pane displays the source data for the same symbol source rows.
- The AAOI symbol has two golden/death cross pairs. The change in close price for one pair is .57 and the change for the other pair is 17.67. As a result, the median is the average of these two values or 9.12.
- The AAXN symbol has three golden/death cross pairs. The middle change value is 3.91, which is the calculated median for the symbol.
- The AMZN symbol has a single row in the ##table_for_median_by_category table with a change in close price of 200.87, which is also the calculated median value in the top pane.
A stored procedure to compute coefficients of determination
The coefficient of determination is an indicator of the goodness of fit of a predicted set of values to an observed set of values. The predicted set of values can come from anywhere, such as a neural network data science algorithm or a multiple linear regression model. From a computational perspective, the coefficient of determination can be represented as the ratio of two sets of computed values.
- The first computed value is the sum of squared deviations of the observed values from the predicted values.
- The second computed value is the sum of squared deviations of the observed values from the mean of the observed values.
- As the ratio of the first computed value gets smaller relative to the second computed value, the predicted values are confirmed to match the observed values more closely.
- If the ratio equals zero, then the fit is perfect.
- If the ratio equals one, the predicted values do not describe the observed values any better than the mean of the observed values.
- As a consequence, the range of possible coefficient of determination values extend from zero through one.
- The mathematical support for this definition of the coefficient of determination is available in several sources including Wikipedia and an exceptionally easy-to-follow blog.
You should note that the general definition of the coefficient of determination does not specify the process for creating predicted values. Additionally, the coefficient of determination definition does not specify anything about the domains of the observed values. However, these kinds of considerations can impact the value of a coefficient of determination. One discussion of potential caveats about how to interpret coefficients of determination appears here.
The coefficient of determination is often represented as R2. In regression analysis, for example, either single or multi-linear regression, the Pearson product moment correlation for regressions is frequently denoted as r. The correlation coefficient represents the association between one or more independent variables relative to a dependent variable.
- A perfect positive correlation is represented by a value of plus one.
- A perfect negative correlation is represented by a value of minus one.
- No correlation is represented by a value of zero.
In the context of regression analysis, the coefficient of determination is the square of the Pearson product moment correlation. However, more specialized assumptions pertain to the product moment correlation (r) than for the coefficient of determination (R2).
- For example, the source of the predicted values for a coefficient of determination need not be a linear regression equation - this is especially so for advanced data science models.
- However, the source of predicted values in many empirical studies for a coefficient of determination is based on some variation of a linear regression equation.
- Therefore, to help you to reconcile this tip to the clear majority of empirical studies reporting coefficients of determination, the computational expression for the coefficient of determination draws on its relationship to linear regression.
In the context of simple linear regression with one independent variable (x) and one dependent variable (y), the Pearson product moment correlation can be computed with an expression based on three underlying terms.
- The sum of cross products of x values from their mean with y values from their mean.
- The square root of the sum of squares of x values from their mean.
- The square root of the sum of squares of y values from their mean.
The expression below combines these underlying terms in the following formulation for r.
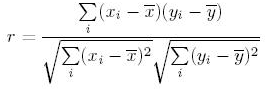
Here's a create procedure statement based on the preceding expression.
- It derives values from the ##temp_xy table. This table contains one row for each pair of x and y values.
- x with a bar denotes the average x value (avg_x).
- y with a bar denotes the average y value (avg_y).
- x and y values are casted as float data types.
- Cross joins are used to add avg_x and avg_y to the set of x and y values.
- Then, the sum of cross products and the sum of the x and y squared deviation terms are computed.
- After the correlation coefficient is computed as a ratio of the sum of cross products to the square root of squared x deviations and square root of squared y deviations, the coefficient of determination is computed as the square of the correlation coefficient.
create procedure compute_coefficient_of_determination
as
begin
set nocount on;
-- compute coefficient of determination
-- based on correlation coefficient
select
sum(y_minus_mean_sq) sum_of_y_sq_devs,
sum(x_minus_mean_sq) sum_of_x_sq_devs,
sum(x_y_mean_product) sum_of_xy_product_devs,
sum(x_y_mean_product) / ( sqrt(sum(y_minus_mean_sq)) * sqrt(sum(x_minus_mean_sq)) ) correlation_coefficient,
power(sum(x_y_mean_product) / ( sqrt(sum(y_minus_mean_sq)) * sqrt(sum(x_minus_mean_sq)) ), 2) coefficient_of_determination
from
(
-- compute power deviations from mean
select
x,
y,
( x - avg_x ) x_minus_mean,
power(( x - avg_x ), 2) x_minus_mean_sq,
( y - avg_y ) y_minus_mean,
power(( y - avg_y ), 2) y_minus_mean_sq,
( x - avg_x ) * ( y - avg_y ) x_y_mean_product
from
(
-- inputs for coefficient of determination
select *
from (select cast(x as float) x, cast(y as float) y from ##temp_xy) source_date
cross join (select avg(cast(y as float)) avg_y from ##temp_xy) avg_y
cross join (select avg(cast(x as float)) avg_x from ##temp_xy) avg_x
) for_r_squared_inputs
) for_r_squared
return
end
The next script shows code for computing a correlation coefficient for a set of x and y values with a negative correlation from a prior MSSQLTips.com tip on correlation coefficients. This set of x and y values is from the "Pearson Negative Correlation Example" section within the tip. Although the expression for the correlation coefficient is different in this tip than the prior tip, the computed value is the same for all practical purposes (the same to within -.000000000000001). Additionally, this tip extends the prior tip by adding the coefficient of determination which was not computed by the prior tip. The results also empirically demonstrate the relationship between the correlation coefficient and the coefficient of determination.
-- create and populate ##temp_xy begin try drop table ##temp_xy end try begin catch print '##temp_xy not available to drop' end catch create table ##temp_xy ( --pkID integer identity(1,1) primary key, x float, y float ) go -- sample pearson product moment correlation data -- with negative correlation -- from --https://www.mssqltips.com/sqlservertip/4544/calculating-the-pearson-product-moment-correlation-coefficient-in-tsql insert into ##temp_xy values (1.581662726, 29.65152293) insert into ##temp_xy values (3.4369907, 28.01601842) insert into ##temp_xy values (5.20372199, 26.64762377) insert into ##temp_xy values (6.548564275, 25.52941989) insert into ##temp_xy values (8.236812206, 24.46357622) insert into ##temp_xy values (9.37715358, 22.94984262) insert into ##temp_xy values (10.51055702, 21.25097239) insert into ##temp_xy values (11.82382087, 19.31299184) insert into ##temp_xy values (13.40427251, 17.97538895) insert into ##temp_xy values (15.24348405, 16.23958242) insert into ##temp_xy values (16.64768328, 14.69010224) insert into ##temp_xy values (18.04064143, 12.86494034) insert into ##temp_xy values (19.51671012, 11.4152393) insert into ##temp_xy values (20.58177787, 10.30092096) insert into ##temp_xy values (22.04140726, 8.625347334) insert into ##temp_xy values (23.81958423, 6.721438358) insert into ##temp_xy values (25.02552769, 5.340616899) insert into ##temp_xy values (26.9841361, 3.958114624) insert into ##temp_xy values (28.04718847, 2.624742871) insert into ##temp_xy values (29.6213496, 1.264092442) select * from ##temp_xy exec dbo.compute_coefficient_of_determination
This screen shot shows the output from the preceding script.

The next script draws on a web page posted by professor Michael T. Brannick from the University of South Florida on estimating parameters for a simple linear regression model. His web page regresses person weight on person height. Height specified in inches is used as the x variable, and weight is specified in pounds as the y variable. The professor's web page shows how to estimate the slope and intercept for estimating a person's weight from their height. We'll explore the web page more thoroughly in the next section. However, the page is relevant for this section because it does present a correlation coefficient for a set of weights and their associated heights.
The following code excerpt shows the weight and height values along with a call to the compute_coefficient_of_determination stored procedure. This code excerpt assumes the ##temp_xy table is already created and populated, such as from the prior example. Therefore, it starts by deleting all values from the ##temp_xy table. Then, it populates the table with the values from professor Brannick's web page.
delete from ##temp_xy -- sample regression data -- from --http://faculty.cas.usf.edu/mbrannick/regression/regbas.html insert into ##temp_xy values (61, 105) insert into ##temp_xy values (62, 120) insert into ##temp_xy values (63, 120) insert into ##temp_xy values (65, 160) insert into ##temp_xy values (65, 120) insert into ##temp_xy values (68, 145) insert into ##temp_xy values (69, 175) insert into ##temp_xy values (70, 160) insert into ##temp_xy values (72, 185) insert into ##temp_xy values (75, 210) select * from ##temp_xy exec dbo.compute_coefficient_of_determination
Here's the bottom line output from the script. You can cross check the computed correlation coefficient from the script with the reported correlation value from the web page. They match to within rounding error to a value of .94. The output from the stored procedure also includes the coefficient of determination. Recall that this is square of the correlation coefficient.

A stored procedure to compute the slope and intercept
You just learned how to assess the strength of the relationship among a set of paired x and y values. This section grows your ability to characterize the relationship for the paired x and y values by providing a stored procedure to estimate a slope and an intercept for a regression line through the paired values. This kind of relationship is sometimes described as a simple linear regression because it fits the dependent variable (y) to just one independent variable (x) as opposed to two or more independent variables.
Because the correlation coefficient contains information about the strength and type of a relationship (positive or negative), you can use it as a starting point for estimating the slope and intercept for a line regressed through a set of x and y values.
One useful way of conceptualizing the regressed line through a set of paired yi and xi values is with the following expression.
- The yi values denote the dependent variable for each pair of values.
- The xi values denote the independent variable for each pair of values.
- The i values extend from 1 through n where n is the number of paired values.
- The slope represents a best estimate value for mapping changes in the independent variable to changes in the dependent variable.
- The intercept is an offset value for characterizing how to raise or lower the slope times xi values to best match their corresponding yi values.
- The residual equals the difference between the observed yi value and slope times xi value plus intercept. For least squares regression, the sum of the squared residuals decreases as the coefficient of determination for a set of paired yi and xi values grows.
yi = slope*xi + intercept + residual
Professor Brannick's web page describes two methods for estimating the slope and intercept based on simple linear regression. This tip illustrates the implementation of the first method, which relies on the correlation coefficient, the average for the xi values, and the average for the yi values.
- Equation 2.4 on the web page estimates the slope as the product of the correlation
coefficient times the ratio of the sample standard deviation for the yi
values divided by the sample standard deviation of the xi values.
- The outputs from the compute_coefficient_of_determination stored procedure from the preceding section includes the correlation coefficient for a set of paired yi and xi values.
- The SQL Server built-in stdev function can compute the sample standard deviation for a set of values, such as the yi and xi values on which a regression is based.
- Equation 2.5 on the web page presents an approach to estimating the intercept based on the slope for a regression line and the mean of yi and xi values. You can use the SQL Server avg function for computing mean of each set of values.
The following script packages some T-SQL code in a stored procedure for computing the slope and intercept of a regression line. The implementation relies on a set of nested queries and a global temporary table named ##temp_xy; the exact code for populating this table appears in a subsequent script and follows the general approach described in the preceding section.
- The inner most query named xy returns a result set with all paired yi and xi values from the ##temp_xy table. The result set has a separate row for each pair of yi and xi values in ##temp_xy table.
- Next, an outer query uses the yi and xi values with the stdev function to compute the sample standard deviation of the yi and xi values, respectively. The result set from this query has a single row with one column for the standard deviation of the yi values and another column for the standard deviation of the xi values.
- A subsequent outer query adds the correlation coefficient and coefficient of determination to its result set along with the two standard deviations. The correlation coefficient and coefficient of determination are derived from the ##r_squared_outputs table, which, in turn, is output by the compute_coefficient_of_determination stored procedure. Therefore, to run the compute_slope_intercept_correlation_coefficient stored procedure successfully, you must first invoke the compute_coefficient_of_determination stored procedure.
- The next outer query computes the slope based on the two standard deviations and the correlation coefficient. This outer query also adds two new column values - one for the mean of the xi values and another for the mean of the yi values.
- Finally, the outermost query displays the slope, intercept, correlation coefficient, and coefficient of determination.
create procedure compute_slope_intercept_correlation_coefficient
as
begin
select
slope
,(avg_y - (slope * avg_x)) intercept
,[correlation coefficient]
,[coefficient of determination]
from
(
select
(r*(s_y/s_x)) slope
,r [correlation coefficient]
,[coefficient of determination]
,(select avg(x) from ##temp_xy) avg_x
,(select avg(y) from ##temp_xy) avg_y
from
(
select
s_y
,s_x
,(select correlation_coefficient from ##r_squared_outputs) [r]
,(select coefficient_of_determination from ##r_squared_outputs) [coefficient of determination]
from
(
select
s_y
,s_x
from
(
select
stdev(x) s_x
,stdev(y) s_y
from
(
select
x
,y
from ##temp_xy
) xy
) for_s_y_and_s_x
) s_y_and_s_x
) slope
) slope_and_intercept_and_fit
return
end
The next script shows an example of using the compute_slope_intercept_correlation_coefficient stored procedure with the sample data presented in professor Brannick's web page for the regression of weight in pounds (yi) on height in inches (xi).
- The script starts by creating a fresh copy of the ##temp_xy table and populating it with ten pair of xi and yi value pairs. These data are from professor Brannick's web page.
- Next, the script prepares a fresh copy of the ##r_squared_outputs table. The purpose of this table is to save outputs from the compute_coefficient_of_determination stored procedure.
- Then, the compute_coefficient_of_determination stored procedure is invoked, and its output is preserved in the ##r_squared_outputs table.
- Finally, the compute_slope_intercept_correlation_coefficient stored procedure is run. This outputs the slope and intercept for the fitted line passing through the points in the ##temp_xy table. The stored procedure also outputs two goodness of fit metrics - namely, the correlation coefficient and the coefficient of determination.
-- create and populate ##temp_xy begin try drop table ##temp_xy end try begin catch print '##temp_xy not available to drop' end catch create table ##temp_xy ( --pkID integer identity(1,1) primary key, x float, y float ) go delete from ##temp_xy -- sample regression data -- from --http://faculty.cas.usf.edu/mbrannick/regression/regbas.html insert into ##temp_xy values (61, 105) insert into ##temp_xy values (62, 120) insert into ##temp_xy values (63, 120) insert into ##temp_xy values (65, 160) insert into ##temp_xy values (65, 120) insert into ##temp_xy values (68, 145) insert into ##temp_xy values (69, 175) insert into ##temp_xy values (70, 160) insert into ##temp_xy values (72, 185) insert into ##temp_xy values (75, 210) -- create a fresh copy of the ##r_squared_outputs -- to store outputs from the stored procedure to -- compute the coefficient of determinaton and -- correlation coefficient begin try drop table ##r_squared_outputs end try begin catch print '##r_squared_outputs not available to drop' end catch create table ##r_squared_outputs ( sum_of_y_sq_devs float ,sum_of_x_sq_devs float ,sum_of_xy_product_devs float ,correlation_coefficient float ,coefficient_of_determination float ) go -- Finally, invoke the compute_coefficient_of_determination -- stored procedure followed by the compute_slope_intercept_correlation_coefficient -- stored procedure insert ##r_squared_outputs exec dbo.compute_coefficient_of_determination exec dbo.compute_sl
The next screen displays the output from the preceding script. Notice, in particular, the slope and intercept column values. You can use these values to represent the fitted line through the yi and xi value pairs. The expression for the observed weights in pounds based on the height in inches equals
6.97 * height - 316.86

Two stored procedures for assessing the difference between means
The t test statistic is widely used for evaluating whether the difference between two group means or two sets of measurements for the same group are statistically different. Wikipedia offers an introductory survey on the various uses of the t statistic. The same survey also offers a range of expressions appropriate for computing t values in different contexts, such as for assumptions about the distribution of data values and ways to compare data.
For example, two different web page designs (an old one versus a revised one) at a selection of different locations throughout a website can each make a request for users to submit their email addresses in exchange for different incentives. If the average percent submitting addresses with the new web page design is greater than with the old web page design, then it may be worth switching to the new incentive for a whole range of different offers from a company's website. The t statistic offers an objective way of assessing if any observed difference between groups is a non-chance occurrence. Statistically significant t statistic values vary according to the size of the sample data, the probability level at which you require a confirmation for a statistically significant difference, and the type of comparison that you want to perform.
- Larger samples require lower t statistic values to confirm a statistically significant outcome because the means and sample variability is more stable for larger samples.
- If you require confirmation at the five percent probability level versus the one percent probability level, then a lower t statistic will qualify an outcome as statistically significant. Conversely, confirmation at the one percent probability level requires a higher t value.
- The distribution of t values has upper and lower tails around a central value.
- Therefore, if the means for two groups qualify as different no matter which mean is larger, a smaller t value is required for statistical significance. This kind of comparison is called a two-tailed test.
- On the other hand, if one group must have a larger mean than the other group for the group means to be accepted as statistically different, then a larger t value is required. This kind of comparison is called a one-tailed test.
- There are many published tables of t values from which you can assess the statistical significance of a t value. This tip uses one published by NIST/SEMATECH in an e-Handbook of Statistical Methods. The link for the t statistic table and an explanation of how to use its published values for one-tailed and two-tailed tests is available here. NIST and SEMATECH are abbreviations for two distinct organizations that collaborated for the handbook's preparation. NIST is for the National Institutes of Standards and Technology, and SEMATECH is a not-for-profit consortium that performs research and development to advance chip manufacturing.
This tip demonstrates how to compute t values for two different types of t tests. There are other types that are more or less distinct from the two kinds computed in this tip. For your easy reference and validation of the t statistic values in the T-SQL scripts presented within this section, sample data is drawn from a web resource posted by professor Martin A. Lindquist during the time that he served as a faculty member at Columbia University in New York City.
- The first t test is for the difference in means between two distinct samples with the same sample size and assuming the same sample variance. The stored procedure implementing this kind of test is used for measures of reaction time to a signal after the administration of either a treatment drug or a placebo. Persons in one group are administered the treatment drug, and persons in the other group are administered the placebo.
- The second t test is for the difference between two sets of paired measurements on a set of cars. One set of miles-per-gallon measures were recorded when using premium gasoline, and the other set of measurements were recorded for regular gasoline. Therefore, each car contributed two miles-per-gallon results - one with regular gasoline and the other with premium gasoline.
The source data for the difference between two group means appears below. Notice there are twelve rows. Six with a group_id value of Group_1 and six more with a group_id value of Group_2. The scores are reaction times to a signal; smaller values indicate faster response times. Group_1 scores are for persons to whom the placebo was administered. Group_2 scores are persons to whom the treatment drug was administered.
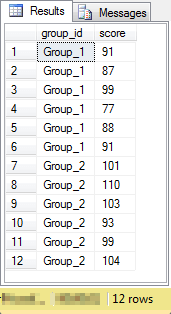
The hypotheses for the test of the difference between the group means is based on a one-tailed test. The treatment drug is expected to slow reaction time. So, the null hypothesis is for no difference between the group means. On the other hand, the alternative hypothesis is for reaction times to be longer for the group to whom the treatment drug was administered. Therefore, the mean of Group_1 scores should be smaller than the mean of Group_2 scores. The degrees of freedom for this sample of scores is ten, which is the sum of the two group sample sizes less one for each group. According to Wikipedia, the expression for the t statistic comparing the means between the two groups is as follows.
- The two X-bar terms are the means for Group_1 and Group_2 respectively.
- Sp represents the pooled standard deviation. The Sp is the square root of the average sample variance across each of the two groups.
- Recall that in this example that the sample size is six in each group. Therefore, the value of n is six.
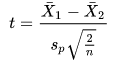
The following script creates the compute_t_between_2_groups stored procedure. The code implements the steps described above.
- Means for each group are computed (the two X-bar values); then the difference between the two means is computed.
- The count for each group is computed.
- Sample standard deviations for each group are computed and these quantities are squared for the sample variances of each group.
- Then, the pooled standard deviation (Sp) is computed.
- Next, the difference between the means is divided by the pooled standard deviation weighted by square root of 2 divided by n where n is sample size per group.
- Finally, a single row of output is generated with column headers describing the column values.
create procedure compute_t_between_2_groups
as
begin
set nocount on;
-- compute t for difference in means between 2 groups
-- sample size (n) assumed to be same in both groups
-- both groups have same sample variance
select top 1
avg_of_group_scores.avg_by_group avg_group_1
,lead(avg_of_group_scores.avg_by_group,1)
over (order by avg_of_group_scores.group_id) avg_group_2
,(avg_of_group_scores.avg_by_group - lead(avg_of_group_scores.avg_by_group,1)
over (order by avg_of_group_scores.group_id)) mean_difference
,(avg_of_group_scores.avg_by_group - lead(avg_of_group_scores.avg_by_group,1)
over (order by avg_of_group_scores.group_id))
/ (pooled_stdev.pooled_stdev * sqrt((cast (2 as float)) /cast(count_of_group_scores.count_by_group as float))) computed_t
,count_of_group_scores.count_by_group + lead(count_of_group_scores.count_by_group,1)
over (order by count_of_group_scores.group_id) -2 df
from
(
select
group_id
,avg(score) avg_by_group
from ##temp_group_scores
group by group_id
) avg_of_group_scores
inner join
(
select
group_id
,stdev(score) stdev_by_group
from ##temp_group_scores
group by group_id
) stdev_of_group_scores
on avg_of_group_scores.group_id = stdev_of_group_scores.group_id
inner join
(
select
group_id
,count(*) count_by_group
from ##temp_group_scores
group by group_id
) count_of_group_scores
on avg_of_group_scores.group_id = count_of_group_scores.group_id
cross join
(
select
sqrt(sum(sq_stdev_by_group)/2) pooled_stdev
from
(
select
power(stdev(score),2) sq_stdev_by_group
from ##temp_group_scores
group by group_id
) for_pooled_stdev
) pooled_stdev
return
end
The following screen shot displays the result set output by the stored procedure.
- The first two column values are for the means for Group_1 and Group_2, respectively.
- The third column value is for the difference between the means.
- The fourth column value is for the computed t statistic for the mean difference.
- The fifth column denotes the degrees of freedom to use when referencing a published table of significant t values at different degrees of freedom and probability levels.

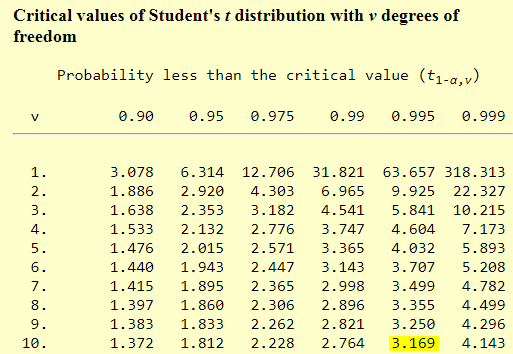
The following excerpt from the NIST/SEMATECH published table of statistically significant t values has highlighting added for this tip. The highlighting is for the t value of 3.169, which is the statistically significant t value for 10 degrees of freedom at the .005 probability level in a one-tailed test. Because our computed t value has an absolute value of 3.446, the placebo group has a mean value that is statistically less than the treatment group at beyond the .005 probability level. In the worked example from professor Martin's web page, he reports the probability level of the difference between the means more precisely at .003, which concurs generally with our outcome. Professor Martin's outcome is likely more precise because he used a specialized calculator or a simulator for more precise probability values associated with t values than is commonly provided by published tables of critical t values. His web page did not indicate the means by which he derived a probability level of .003.
The following screen shot shows the raw data for a paired difference t test. There are ten rows in the result set one for each of ten cars labeled as subject_1 through subject_10. The apply_1_result column is for miles-per-gallon using premium gasoline. The apply_2_result column is for miles-per-gallon using regular gasoline. Notice that the mile-per-gallon result is nearly always greater when premium gasoline is used instead of regular gasoline.
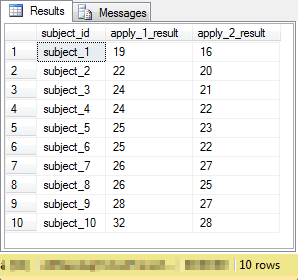
Wikipedia offers the following equation for computing a t value when paired differences are contrasted, such as in the preceding screen shot.
- The X-bar value with a D subscript is for the mean difference between the paired measurements.
- The sD term is the sample standard deviation of the paired differences. You can use the SQL Server built-in stdev function to compute this quantity.
- The n value is for the number of paired differences; this value is ten for our sample data.
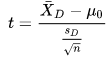
The degrees of freedom for the above t statistic is the number of paired differences less one. This is nine for the sample data.
The following script shows the create procedure statement for a stored procedure to compute a t statistic value for a set of paired differences.
- The innermost query named for_t_inputs computes the difference for each pair of miles-per-gallon measurements. There is one row for each subject (car) in the innermost query's result set.
- The next query out, named for_t_value, uses the differences from the innermost query to compute the overall average difference and the sample standard deviation of the differences. This middle level query also counts the number of paired measurements. There is just one row in the result set for this middle level query.
- Finally, the outermost query reports the overall average difference, the computed t value for the paired differences, and the degrees of freedom to assist in evaluating the statistical significance of the differences.
create procedure compute_paired_sample_t
as
begin
set nocount on;
-- compute paired sample t value based on
-- values in the ##temp_subject_id_results table
select
avg_difference
,avg_difference/ (stdev_difference/sqrt(cast(obs as float))) computed_t
,obs-1 df
from
(
select
avg(difference) avg_difference
,stdev(difference) stdev_difference
,count(*) obs
from
(
-- compute subject differences
select
subject_id
,apply_1_result
,apply_2_result
,(apply_1_result - apply_2_result) difference
from ##temp_subject_id_results
) for_t_inputs
) for_t_value
return
end
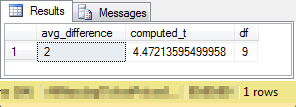
This last screen shot is for the result set from the compute_paired_sample_t stored procedure with the data for the second t test. There are just three columns of output in a single row.
- The first column is for the average difference between the paired values for all subjects in the sample. The premium gasoline delivered on average two more miles per gallon than regular gasoline.
- The next column is for the computed t value. With our sample data, the computed t is 4.4721…
- The last column is for the degrees of freedom, which is nine for our sample data.
From the preceding critical values t distribution table from the NIST/SEMATECH data source, you can tell that the computed t is significant beyond .001 probability level for a one-tailed test. Clearly, the cars in the sample delivered statistically more miles per gallon when using premium gasoline than when using regular gasoline. This is because the critical t value for significance at the .001 probability level for nine degrees of freedom is 4.269, but the t value for the paired difference was even greater at beyond 4.4721. In other words, there was less than one chance in a thousand that this t value could be attained if premium gasoline did not deliver better miles per gallon results than regular gasoline!
Next Steps
There are four script files available for download with this tip. Each file corresponds to one of the four sections on computing a type of statistic.
The script files for three sections are stand-alone, but the script file for the section on computing medians is dependent on external data from another tip.
- For the stand-alone script files, all data that you need to compute statistics are in the script file. You can update the data with your own custom data.
- For the script file on computing medians, you need to download data from here for a database of all NASDAQ closing prices and a table of moving averages for those closing prices. Code to populate the source data global temporary table with data for golden crosses and death crosses is in the 'script for median overall and by category variable.sql' file. The median examples are meant to show you how to integrate the statistics stored procedures into a T-SQL application as well as how to compute medians under two different scenarios.
About the author
 Rick Dobson is an author and an individual trader. He is also a SQL Server professional with decades of T-SQL experience that includes authoring books, running a national seminar practice, working for businesses on finance and healthcare development projects, and serving as a regular contributor to MSSQLTips.com. He has been growing his Python skills for more than the past half decade -- especially for data visualization and ETL tasks with JSON and CSV files. His most recent professional passions include financial time series data and analyses, AI models, and statistics. He believes the proper application of these skills can help traders and investors to make more profitable decisions.
Rick Dobson is an author and an individual trader. He is also a SQL Server professional with decades of T-SQL experience that includes authoring books, running a national seminar practice, working for businesses on finance and healthcare development projects, and serving as a regular contributor to MSSQLTips.com. He has been growing his Python skills for more than the past half decade -- especially for data visualization and ETL tasks with JSON and CSV files. His most recent professional passions include financial time series data and analyses, AI models, and statistics. He believes the proper application of these skills can help traders and investors to make more profitable decisions.This author pledges the content of this article is based on professional experience and not AI generated.
View all my tips






