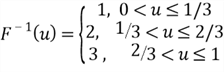By: Nai Biao Zhou | Comments (3) | Related: > TSQL
Problem
Dr. Dallas Snider [1], a MSSQLTips author, mentioned that SQL Server RAND() function could generate random values uniformly distributed from 0 through 1, exclusive. He generated random numbers from the normal distribution with a specific mean and standard deviation [1]. In his other tip [2], he created a function to generate random values in a range. Using SQL Server RAND function for generating random variables from specific probability distributions is a popular topic on the web. Many professionals, for example Dwain Camps [3], have provided excellent solutions. With so many solutions available, we need to find one that fits our requirements. To select effective techniques and examine their performances, database professionals would like to know the principles behind these techniques.
Solution
The notion of "completely random" on an interval means every value
in the interval has an equal chance to be chosen. If the SQL Server RAND() function
returns a completely random number between 0 and 1, we say that the function has
the uniform distribution on the interval (0,1), denoted by
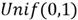 .
Dwain [3] examined the distribution of uniform random numbers generated by SQL Server
RAND() function. He concluded that the uniformity is not great, but probably good
enough for noncritical purposes [3]. In this tip, we assume SQL server RAND() function
can produce a completely random number between 0 and 1, exclusive.
.
Dwain [3] examined the distribution of uniform random numbers generated by SQL Server
RAND() function. He concluded that the uniformity is not great, but probably good
enough for noncritical purposes [3]. In this tip, we assume SQL server RAND() function
can produce a completely random number between 0 and 1, exclusive.
The universality of the uniform, a remarkable characteristic of the uniform distribution,
allows us to construct a random variable with any continuous distribution from a
given
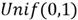 [4]. This characteristic also has several other names, for example inverse transform
sampling. We will use T-SQL to generate random numbers from continuous distributions
and discrete distributions by using the universality of the uniform theorem.
[4]. This characteristic also has several other names, for example inverse transform
sampling. We will use T-SQL to generate random numbers from continuous distributions
and discrete distributions by using the universality of the uniform theorem.
This tip is organized as follows. In section 1, we explore concepts of random variable and distribution. Section 2 introduces three named discrete probability distributions. We look at two named continuous probability distributions in section 3. Next, in section 4, we give practice in the use of the universality of the uniform theorem for generating random variables from specific probability distributions. In this tip, T-SQL is used to produce random numbers, and R is used to create graphic representations. The sections build on each other. Information presented early in the tip will be helpful for generating random numbers in the later sections.
All the source codes used in this tip were tested with SQL Server Management Studio V17.4, Microsoft Visual Studio Community 2017, Microsoft R Client 3.4.3, and Microsoft ML Server 9.3 on Windows 10 Home 10.0 <X64>. The DBMS is Microsoft SQL Server 2017 Enterprise Edition (64-bit).
1 – Basic Concepts
The following T-SQL statements are used to randomly choose an integer value between 1 and 3, inclusive:
-- Declare and initialize variables DECLARE @lower_limit INT = 3 DECLARE @upper_limit INT = 1 -- Choose a random integer between @lower_limit and @upper_limit, inclusive SELECT ROUND((@upper_limit - @lower_limit) * RAND(CHECKSUM(NEWID())), 0) + @lower_limit
Intuitively, these T-SQL statements completely randomly selected one of these three integers. In other words, all these integer numbers have an equal chance of being choosen. I wrote a script in R that ran these SQL statements 10,000 times and then loaded those chosen numbers into a data frame. I plotted a bar chart of the frequency distribution for these numbers to visualize the chance of occurrence of each integer number.
# Reset the compute context to your local workstation.
rxSetComputeContext("local")
# Define connection string to SQL Server
sql.server.conn.string <- "Driver=SQL Server;Server=.Database=TutorialDB;Trusted_Connection={Yes}"
# Execute T-SQL statements through an RxSqlServerData data source object
data.source.object <- RxSqlServerData(sqlQuery = "
SELECT top 10000
u.random_value,
(ROUND((3-1)*u.random_value, 0)+1) as random_integer
FROM sys.all_columns a1
CROSS APPLY sys.all_columns a2
CROSS APPLY
(
SELECT RAND(CHECKSUM(NEWID())) as random_value
) u",
connectionString = sql.server.conn.string)
# Read the result into a data frame in the local R session.
data.frame.random.numbers <- rxImport(data.source.object)
# Create a Frequency Distribution Bar Chart quickly with the plot() function
# when the categorical variable to be plotted is a factor or ordered factor.
plot(as.factor(data.frame.random.numbers$random_integer),
main = "Frequency Distribution of Randomly Selected Integers Between 1 and 3",
xlab = "Random Integer",
ylab = "Number of Occurrence",
col = "blue")
The bar chart, shown in Figure 1, illustrates that the chance of selecting integer number "2" is twice as many chances as other two integers. This concludes that the preceding SQL statements cannot generate completely random integers on an interval.
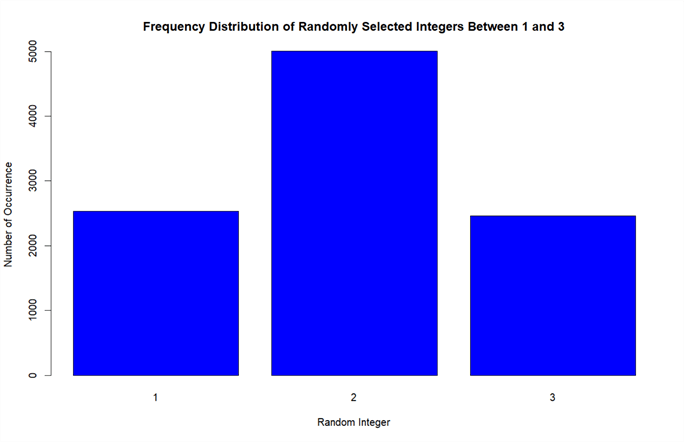
Figure 1 Frequency Distribution of Random Integers Between 1 and 3 Generated by SQL Server RAND Function
Sometimes, we may be required to randomly pick a number from an integer array in which elements are not consecutive, furthermore, each element may have a different probability to be chosen. These tasks become complicated. I do not think we can tackle these tasks without understanding of random variables and their distributions. We will walkthrough these concepts in this tip.
1.1 Random variables
When we consider something random, mostly we mean all the people or things involved
have an equal chance of being chosen. When we describe events as random, we mean
that a definite plan or pattern is not followed [6]. The Collins online dictionary
states that a variable is a factor that can change in quality, quantity, or size,
which we must consider in a situation [7]. Putting all together these definitions,
we can consider a random variable a symbol that can represent a random selected
number, categories, etc. This kind of definition does not tell where randomness
comes from. To make the notion of random variable both conceptually and technically
correct, we define it as a function mapping the sample space to a set of real numbers
[4]. Professor Jost also gave an informal definition: a random variable is a process
for choosing a random number [5]. We often denote random variables by capital letters,
for example
 .
A random variable numerically describes outcomes of an experiment and reveals some
aspects of the experiment.
.
A random variable numerically describes outcomes of an experiment and reveals some
aspects of the experiment.
In the experiment of rolling a balanced die, the sample space is {1 spot, 2 spots,
3 spots, 4 spots, 5 spots, 6 spots}. Let
 be the remainder after division of the number of spots by 3. Then,
be the remainder after division of the number of spots by 3. Then,
 is a random variable with possible values 0, 1, and 2. Let
is a random variable with possible values 0, 1, and 2. Let
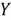 be the quotient. The possible values of
be the quotient. The possible values of
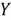 are 0, 1 and 2. Let
are 0, 1 and 2. Let
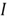 be 1 if the remainder is 0 and 0 otherwise. Since the random variable
be 1 if the remainder is 0 and 0 otherwise. Since the random variable
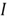 indicates whether the number of spots is evenly divisible by 3, we also call this
kind of random variable an indicator random variable. The mapping from the sample
space to the set of real numbers is shown in Table 1.
indicates whether the number of spots is evenly divisible by 3, we also call this
kind of random variable an indicator random variable. The mapping from the sample
space to the set of real numbers is shown in Table 1.
| Number of Spots (s) | Possible Values of X | Possible Values of Y | Possible Values of I |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 2 | 0 | 0 |
| 3 | 0 | 1 | 1 |
| 4 | 1 | 1 | 0 |
| 5 | 2 | 1 | 0 |
| 6 | 0 | 2 | 1 |
Table 1 The Random Variables X, Y and I Defined on the Sample Space
Table 1 reveals the fact that multiple random variables can be defined on the
same sample space, and one experiment outcome may map to several different real
numbers. We have also observed that the randomness in a random variable is due to
the random outcomes of an experiment. The probability of each outcome in the sample
space determines the probability that the random variable will take on a value or
an interval. In addition, we derived an equation for
 ,
,
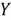 and
and
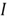 :
:
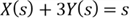
where
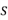 denotes the number of spots.
denotes the number of spots.
Then we write
 in terms of
in terms of
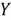 by rearranging the equation:
by rearranging the equation:
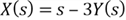 .
These two equations help to reinforce the understanding that random variable is
a function mapping each outcome in sample space to a real number.
.
These two equations help to reinforce the understanding that random variable is
a function mapping each outcome in sample space to a real number.
When a random variable can take on only a finite set of numeric values or an
infinite sequence, we name this variable discrete random variable. The set of values
is called the support of the discrete random variable. On the other side,
when a random variable can take any numeric values in an interval, possibly infinite,
for example,
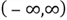 ,
the variable is named as a continuous random variable.
,
the variable is named as a continuous random variable.
1.2 Distributions
In the example of choosing one number from three consecutive integers, we expected to select a completely random integer number. However, the bar chart in Figure 1 argued that those chosen integer numbers are not uniformly distributed. The behavior of expected random numbers is different from those actual generated random numbers. We can describe this kind of difference by using the language of probability, that is distribution. The distribution of a random variable specifies the probabilities of all events associated with this random variable [4], consequently, describes the behavior of the random variable.
1.2.1 Probability Mass Function
For a discrete random variable,
 ,
the probability distribution can be expressed by a probability mass function (hereinafter
referred to as the "PMF"), denoted by
,
the probability distribution can be expressed by a probability mass function (hereinafter
referred to as the "PMF"), denoted by
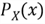 .
This function provides the probability for each possible value of the random variable:
.
This function provides the probability for each possible value of the random variable:
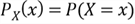
where
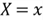 denotes an event that maps to a subset of the sample space.
denotes an event that maps to a subset of the sample space.
In the experiment of rolling a balanced die, demonstrated in Table 1,
 is the remainder after division. The possible experiment outcomes, 1 spot and 4
spots, in the sample space map to the integer value 1 of the support of
is the remainder after division. The possible experiment outcomes, 1 spot and 4
spots, in the sample space map to the integer value 1 of the support of
 .
Both subsets, {1 spot, 4 spots} and { 1 }, mean the same event
.
Both subsets, {1 spot, 4 spots} and { 1 }, mean the same event
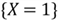 .
Note that
.
Note that
 is a function. We can write the event in another form:
is a function. We can write the event in another form:
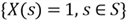 .
Thus, we use naïve definition [4] to calculate the probability of the event:
.
Thus, we use naïve definition [4] to calculate the probability of the event:
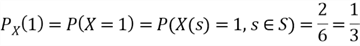
For completeness, we compute the probabilities of all possible values of
 .
All these equations together determine the PMF of
.
All these equations together determine the PMF of
 :
:
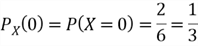
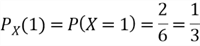
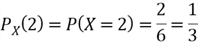
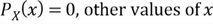
The PMF
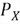 must satisfy the following two conditions:
must satisfy the following two conditions:
- PMF must be nonnegative for each value of the random variable;
- The sum of the probabilities for each value of the random variable must equal to 1.
1.2.2 Cumulative Distribution Functions
In the rolling a die experiment, the random variable
 has 3 possible values: 0, 1 and 2. When the number of possible values increases,
the probability of each value gets smaller, and the effect of noise increases [8].
This limit might be removed by using the cumulative distribution function (hereinafter
referred to as the "CDF"). Unlike the PMF, which is defined for discrete
random variables only, the CDF can describe both discrete random variables and continuous
random variables.
has 3 possible values: 0, 1 and 2. When the number of possible values increases,
the probability of each value gets smaller, and the effect of noise increases [8].
This limit might be removed by using the cumulative distribution function (hereinafter
referred to as the "CDF"). Unlike the PMF, which is defined for discrete
random variables only, the CDF can describe both discrete random variables and continuous
random variables.
The CDF of a random variable
 ,
denoted by
,
denoted by
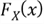 or
or
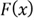 ,
is the function given by:
,
is the function given by:
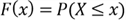
where
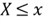 denotes an event that is a subset of the sample space to which
denotes an event that is a subset of the sample space to which
 was assigned a real value less than or equal to
was assigned a real value less than or equal to
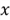 .
.
Shown in Table 1,
 is the remainder after division. The event
is the remainder after division. The event
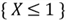 maps to the subset {1 spot, 3 spots, 4 spots, 6 spots} of the sample space. We use
naïve definition [4] to calculate the probability of this event:
maps to the subset {1 spot, 3 spots, 4 spots, 6 spots} of the sample space. We use
naïve definition [4] to calculate the probability of this event:
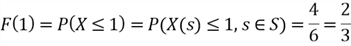
An effective method for deriving a CDF is to convert a PMF to the CDF. The events
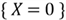 ,
,
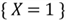 and
and
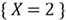 are mutually exclusive events, thus we can use the addition rule:
are mutually exclusive events, thus we can use the addition rule:
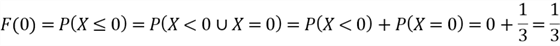
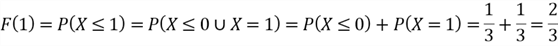
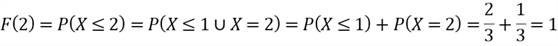
It is observed that a CDF for discrete random variables is not continuous. In addition, the PMF and CDF of a random variable contain the same information. If we have known the CDF of a discrete random variable, we can compute the PDM, for example,
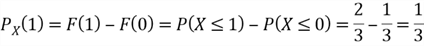
Continuous random variables differ from discrete random variables in that a continuous
random variable
 that takes on any value in an interval. Because there are infinite number of values
that
that takes on any value in an interval. Because there are infinite number of values
that
 could assume, the probability of
could assume, the probability of
 taking on a specific value is 0, that is
taking on a specific value is 0, that is
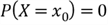 where
where
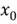 is the specified value. No matter whether we describe a discrete random variable
or a continuous variable, the CDF must satisfy the following three conditions [4]:
is the specified value. No matter whether we describe a discrete random variable
or a continuous variable, the CDF must satisfy the following three conditions [4]:
- The CDF is an increasing function where: if
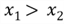 ,
then
,
then
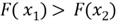 ;
;
- The CDF is continuous from the right, namely, right-continuous;
- The CDF converges to 0 and 1 in the limits;
Now we give the mathematical definitions of a continuous distribution and a continuous random variable: when a CDF of a random variable is differentiable, we consider that the random variable possesses a continuous distribution, and this random variable is a continuous random variable [4].
1.2.3 Probability Density Functions
A probability density function (hereinafter referred to as the "PDF"),
denoted by
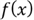 determines a continuous random variable distribution and the CDF does too. They
contain the same information about the continuous random variable distribution.
We have already introduced CDF in section 1.2.2. Given a CDF
determines a continuous random variable distribution and the CDF does too. They
contain the same information about the continuous random variable distribution.
We have already introduced CDF in section 1.2.2. Given a CDF
 of a continuous random variable
of a continuous random variable
 ,
the PDF is the derivative of the CDF:
,
the PDF is the derivative of the CDF:
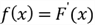
where
 is in the support of
is in the support of
 .
.
Since the CDF is an increasing function and converges to 1 at the upper limit, the PDF of a continuous random variable must satisfy these two criteria:
- PDF must be nonnegative;
- PDF must integrate to 1 over the support of the random variable;
To find the probability of the event,
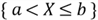 ,
we compute the area on the interval (a, b] under the probability density curve.
Note that the endpoints of the interval have probability 0, therefore the probability
will not change when we include or exclude the endpoints in the computation.
,
we compute the area on the interval (a, b] under the probability density curve.
Note that the endpoints of the interval have probability 0, therefore the probability
will not change when we include or exclude the endpoints in the computation.
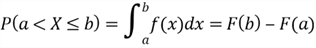
On the other hand, we can derive a CDF from a known PDF:
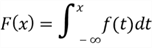
where
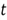 is a dummy variable.
is a dummy variable.
Let’s give a practice in use of CDF and PDF to describe a continuous random
variable. We simulated a continuous random variable
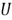 by using SQL function RAND(). The continuous random variable distribution can be
determined by either the CDF or the PDF:
by using SQL function RAND(). The continuous random variable distribution can be
determined by either the CDF or the PDF:
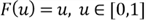
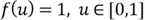
To find the probability of the random variable taking a value less than 0.5,
we compute the area between 0 and 0.5 under the horizontal line
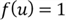 ,
which is a rectangle area.
,
which is a rectangle area.
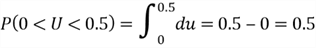
When we generate completely random values by using SQL function RAND(), intuitively, the chance to get a value less than 0.5 is 50%. The intuition agrees with the mathematic calculation.
2 – Discrete Probability Distributions
The distribution of the discrete random variable
 can be expressed with a PMF:
can be expressed with a PMF:
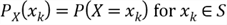
where
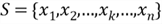 denotes the support of the random variable
denotes the support of the random variable
 ,
,
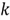 is an integer number, and
is an integer number, and
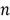 is the size of the sample space. It is noting that
is the size of the sample space. It is noting that
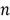 could be infinite.
could be infinite.
By arranging the elements of
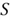 in an ascending order, then we derive the CDF:
in an ascending order, then we derive the CDF:
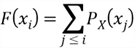
In this section we consider three common distribution functions of discrete random variables: the discrete uniform distribution, the Bernoulli distribution and the binomial distribution.
2.1 The Discrete Uniform Distribution
The discrete uniform distribution is perhaps the simplest discrete probability
distribution [9]. In the experiment of completely randomly choosing a number from
a nonempty finite set of numbers, by adopting the notations used in book [4], let
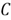 be the set,
be the set,
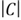 be the size of the set, and
be the size of the set, and
 be the chosen number. The distribution of
be the chosen number. The distribution of
 is a discrete uniform distribution with the parameter
is a discrete uniform distribution with the parameter
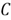 ,
denoted by
,
denoted by
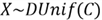 .
Then we have the PMF and CDF of this distribution:
.
Then we have the PMF and CDF of this distribution:
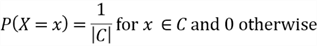
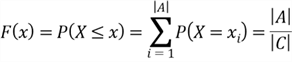
where
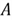 denotes a subset that contains all values in
denotes a subset that contains all values in
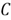 less than or equal to
less than or equal to
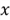 ,
and
,
and
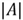 denotes the size of the subset.
denotes the size of the subset.
The discrete uniform distribution is used very often in practice. The example
given in the section 1 tried to generate a random number from the discrete uniform
distribution:
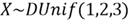 .
.
2.2 The Bernoulli Distribution
A Bernoulli trial is a random experiment that results in only two possible outcomes:
success and failure. The probability of success
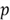 is the same every time the experiment is conducted. The Bernoulli distribution,
denoted by
is the same every time the experiment is conducted. The Bernoulli distribution,
denoted by
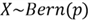 ,
arises from the realization of a single Bernoulli trial [10]. The Bernoulli random
variable
,
arises from the realization of a single Bernoulli trial [10]. The Bernoulli random
variable
 has a value of 1 when success occurs and 0 when failure occurs in a trial. The PMF
is given by:
has a value of 1 when success occurs and 0 when failure occurs in a trial. The PMF
is given by:
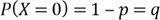
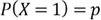
where
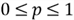 .
.
Any random variables having this PMF possess the Bernoulli distribution with
the parameter
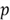 .
Since every event has two states: occur, and fail to occur, a Bernoulli trial is
naturally associated to every event. This kind of Bernoulli random variable, called
the indicator random variable of the event, is often used to simplify problems in
probability, therefore is very useful.
.
Since every event has two states: occur, and fail to occur, a Bernoulli trial is
naturally associated to every event. This kind of Bernoulli random variable, called
the indicator random variable of the event, is often used to simplify problems in
probability, therefore is very useful.
2.3 The Binomial Distribution
In the experiment of performing
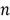 independent Bernoulli trials, the probability of success
independent Bernoulli trials, the probability of success
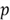 is the same in each trial. The number of successes in the experiment is a discrete
random variable, denoted by
is the same in each trial. The number of successes in the experiment is a discrete
random variable, denoted by
 .
We call the distribution of
.
We call the distribution of
 the binomial distribution with parameters
the binomial distribution with parameters
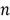 and
and
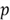 ,
denoted by
,
denoted by
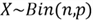 .
In addition to the PMF and CDF, this is the third way to describe a distribution,
which we use a story to explain how the distribution can arise [4]. Then we derive
the PMF from the story:
.
In addition to the PMF and CDF, this is the third way to describe a distribution,
which we use a story to explain how the distribution can arise [4]. Then we derive
the PMF from the story:
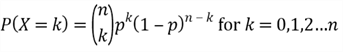
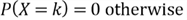
To strengthen the understanding of the binomial distribution, let’s look at the example 6.3 in Stewart’s book [10]:
A grocery store receives a very large number of apples
each day. Since past experience has shown that 5% of them will be bad, the manager
chooses six at random for quality control purposes. Let
 be the random variable that denotes the number of bad apples in the sample. What
values can
be the random variable that denotes the number of bad apples in the sample. What
values can
 assume? For each possible value of
assume? For each possible value of
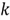 ,
what is the value of
,
what is the value of
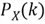 ?
(Stewart, 2009,p 119).
?
(Stewart, 2009,p 119).
When the manager randomly selects an apple, the trial has two possible outcomes: a bad apple or a good apple. The purpose of the experiment is to detect bad apples. When a bad apple is detected, success occurs, and failure occurs otherwise. Since the manager chooses 6 apples from a very large amount that can be considered an indefinitely large, all 6 trials are independent and the probability of success for each trial is constant, that is 5%.
This experiment satisfies the following requirements of being a binomial distribution:
- All trials in the experiment are independent;
- Each trial has two possible outcomes: success and failure;
- The probability of success is the same in each trial;
Therefore,
 has a binomial distribution with parameters
has a binomial distribution with parameters
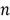 and
and
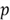 ,
denoted by
,
denoted by
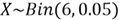 .
The random variable
.
The random variable
 is the random variable that denotes the number of bad apples in the sample. The
variable
is the random variable that denotes the number of bad apples in the sample. The
variable
 can have any value in the set {0, 1, 2, 3, 4, 5, 6}. The PMF is given by:
can have any value in the set {0, 1, 2, 3, 4, 5, 6}. The PMF is given by:
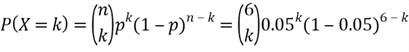
Table 2 shows all probabilities associated with the number of bad apples detected. The probability that the manager finds no bad apples is 0.735. The probability of finding 1 bad apple is 0.232. The chance to find all 6 bad apples is very low.
|
|
| 0 | 0.735 |
| 1 | 0.232 |
| 2 | 0.031 |
| 3 | 2.14e-03 |
| 4 | 8.46e-05 |
| 5 | 1.78e-06 |
| 6 | 1.56e-08 |
Table 2 Binomial PMF for
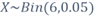
3 – Continuous Probability Distributions
The probability distribution of a continuous random variable is called a continuous probability distribution. A continuous probability distribution differs from a discrete probability distribution in that the continuous probability distribution can be described by a PDF and the discrete probability distribution can be described by a PMF. In this section, we will introduce two well-known continuous distributions: the uniform distribution and the standard normal distribution.
3.1 The Uniform Distribution
We translate the notion "completely random" into a mathematical expression. The following PDF is used to describe a random variable that takes completely random values on a real number interval (a, b):
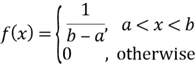
A continuous random variable has the uniform distribution with parameters a and
b on the interval (a, b) when it possesses this PDF. We denote this distribution
by
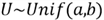 .
The CDF is given by
.
The CDF is given by
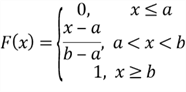
The
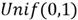 is called standard uniform distribution which has simple PDF and CDF:
is called standard uniform distribution which has simple PDF and CDF:
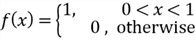
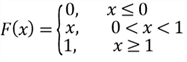
Figure 2 illustrates the PDF and the CDF of the
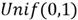 .
We have observed a special characteristic of the uniform distribution on this figure:
partitioning the interval (0,1) into many small subintervals, the probability of
choosing a random value in any subinterval is proportional to the length of the
subinterval. The actual position of the subinterval does not affect the probability.
For example, the chance to take a value in the subinterval (0.0, 0.6) is the same
as in the subinterval (0.3, 0.9), and is three times as many as in the subinterval
(0.5, 0.7).
.
We have observed a special characteristic of the uniform distribution on this figure:
partitioning the interval (0,1) into many small subintervals, the probability of
choosing a random value in any subinterval is proportional to the length of the
subinterval. The actual position of the subinterval does not affect the probability.
For example, the chance to take a value in the subinterval (0.0, 0.6) is the same
as in the subinterval (0.3, 0.9), and is three times as many as in the subinterval
(0.5, 0.7).
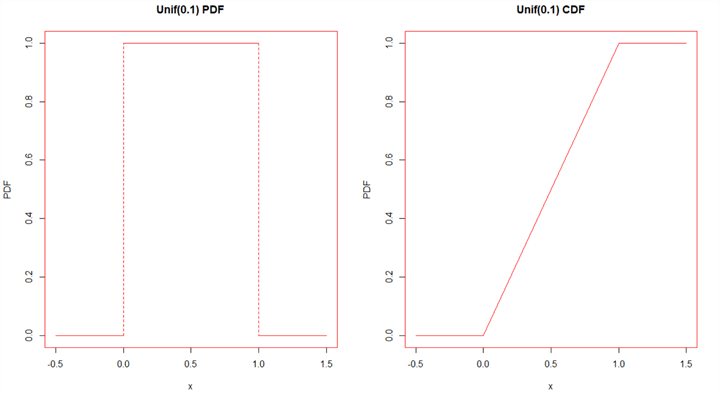
Figure 2 The Probability Density Function and The Cumulative Distribution Function of
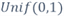 [4]
[4]
3.2 The Standard Normal Distribution
The normal distribution, which has the bell-shaped curve, plays a fundamental
role in statistics. The standard normal distribution, denoted by
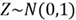 ,
has mean 0 and variance 1. The normal distribution is extremely widely used in statistics
due to the central limit theorem [10]. Since we want to generate test data from
the standard normal distribution later, this section just simply gives the PDF and
CDF of the standard normal distribution.
,
has mean 0 and variance 1. The normal distribution is extremely widely used in statistics
due to the central limit theorem [10]. Since we want to generate test data from
the standard normal distribution later, this section just simply gives the PDF and
CDF of the standard normal distribution.
The PDF and the CDF of the standard normal distribution are given by
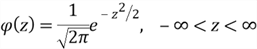
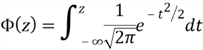
Conventionally, the Greek letter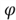 denotes the standard normal PDF,
denotes the standard normal PDF,
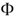 denotes the standard normal CDF, and
denotes the standard normal CDF, and
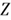 denotes the standard normal random variable.
denotes the standard normal random variable.
4 – Random Number Generator
We have now seen five well-known distributions: the discrete uniform distribution, the Bernoulli distribution, the binomial distribution, the uniform distribution and the standard normal distribution. In this section, random numbers from these distributions will be generated by using SQL server function RAND(). Techniques used in this section can generate random numbers from other distributions as well. Other programming languages can also use these techniques to simulate random variates as long as the uniform pseudo random number generator is available in the programming environment.
4.1 Universality of the Uniform
The universality of the uniform, possessed by the uniform distribution, allows
us to create a random variable from any continuous distribution. On the other hand,
we can transform any continuous distribution into a
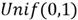 [4]. This property also has several other names, for example inverse transform sampling.
We can produce random values from both continuous distributions and discrete distributions
by using the universality of the uniform theorem.
[4]. This property also has several other names, for example inverse transform sampling.
We can produce random values from both continuous distributions and discrete distributions
by using the universality of the uniform theorem.
The universality of the uniform theorem is the foundation to these random number generation techniques covered in this tip. To precisely present this theorem, I quote it from Hwang & Blitzstein’s book [4]:
(Universality of the Uniform). Let
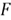 be a CDF which is a continuous function and strictly increasing on the support of
the distribution. This ensures that the inverse function
be a CDF which is a continuous function and strictly increasing on the support of
the distribution. This ensures that the inverse function
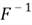 exists, as a function from (0, 1) to
exists, as a function from (0, 1) to 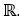 .
We then have the following results.
.
We then have the following results.
- Let
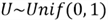 and
and
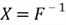 (U).
Then
(U).
Then
 is an r.v. with CDF
is an r.v. with CDF
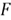 .
.
- Let
 be an r.v. with CDF
be an r.v. with CDF
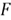 .
Then
.
Then
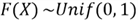 .(
Blitzstein & Hwang, 2015, p205)
.(
Blitzstein & Hwang, 2015, p205)
In their book, "r.v" denotes random variable;
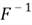 denotes the inverse function of CDF. We have already known the definition of the
CDF:
denotes the inverse function of CDF. We have already known the definition of the
CDF:
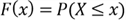
where
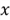 is a real number and
is a real number and
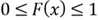 .
.
The function returns the cumulative probability of which the random variable
 takes a value less than or equal to the real number
takes a value less than or equal to the real number
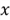 .
In other words, given a real number
.
In other words, given a real number
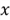 ,
the function returns a value of cumulative probability, denoted by
,
the function returns a value of cumulative probability, denoted by
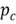 .
Then the inverse function of CDF can be written as
.
Then the inverse function of CDF can be written as
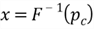
The inverse function returns a real number
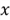 when the cumulative probability value
when the cumulative probability value
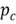 is known. The inverse function tells us what value
is known. The inverse function tells us what value
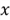 would make the probability of the event
would make the probability of the event
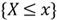 be
be
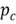 .
For example, a snowblower manufacture investigates engine failure times. They can
use the inverse function of a CDF to compute the time by which 3% of engines would
fail. In this example, the cumulative probability 3% was passed to the inverse function
and the failure time was returned.
.
For example, a snowblower manufacture investigates engine failure times. They can
use the inverse function of a CDF to compute the time by which 3% of engines would
fail. In this example, the cumulative probability 3% was passed to the inverse function
and the failure time was returned.
The first part of the theorem states that, by using the
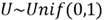 ,
we can create a random variable
,
we can create a random variable
 from any continuous distribution. Let’s prove this:
from any continuous distribution. Let’s prove this:
- Assume an arbitrary continuous distribution with CDF
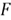 ,
and the inverse function of CDF
,
and the inverse function of CDF
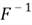 exists;
exists; - Construct a random variable
 by plugging
by plugging
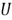 into
into
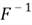 ,
i.e.,
,
i.e.,
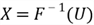 ;
;
- The CDF of the
 distribution is defined by
distribution is defined by
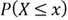 ;
;
- Plug
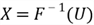 into this definition:
into this definition: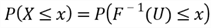
- Since
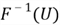 is an increasing function, the inequality
is an increasing function, the inequality
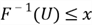 is equivalent to the inequality
is equivalent to the inequality
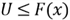 ;
;
- The CDF of the
 distribution from step 5 can be re-written as:
distribution from step 5 can be re-written as:
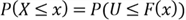
- Since
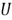 has
has
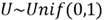 ,
the probability is proportional to the length of the subinterval. That means
,
the probability is proportional to the length of the subinterval. That means
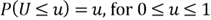 .
Namely,
.
Namely,
 since
since
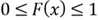 ;
;
- Obtain this equation:
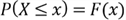 ;
that means the CDF of
;
that means the CDF of
 distribution has the CDF
distribution has the CDF
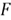 ;
;
Through step 1 to step 8, we have proved that the distribution of the random
variable
 possesses the CDF
possesses the CDF
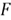 ,
which is the arbitrary distribution, therefore we prove the first part of the theorem.
,
which is the arbitrary distribution, therefore we prove the first part of the theorem.
The second part of the theorem states
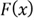 has the standard uniform distribution, i.e.,
has the standard uniform distribution, i.e.,
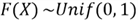 .
We have already known that the values of
.
We have already known that the values of
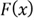 fall within the range [0,1], but we are not sure all possible values are uniformly
distributed on the range.
fall within the range [0,1], but we are not sure all possible values are uniformly
distributed on the range.
To prove this part, we will use a fact that a function of a random variable is
a random variable [4]. Since
 is a random variable and
is a random variable and
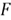 is a function,
is a function,
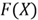 is a random variable. It is noting that a function of discrete random variables
is still discrete. The second part of this theorem does not work for discrete random
variables.
is a random variable. It is noting that a function of discrete random variables
is still discrete. The second part of this theorem does not work for discrete random
variables.
Let a random variable
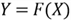 .
Then, we verify that
.
Then, we verify that
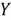 has the standard uniform distribution:
has the standard uniform distribution:
- Assume a continuous distribution with CDF
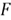 ,
and the inverse function of CDF
,
and the inverse function of CDF
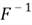 exists;
exists; - Define the random variable
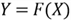 and the CDF of
and the CDF of
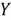 is
is
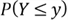 ;
;
- Plug
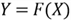 into
into
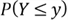 ,
then
,
then
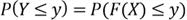 ;
;
- Since
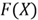 is an increasing function, the inequality
is an increasing function, the inequality
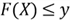 is equivalent to the inequality
is equivalent to the inequality
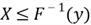 ;
;
- The CDF of
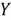 from step 3 can be re-written as
from step 3 can be re-written as
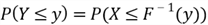
- Since
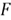 is CFD of
is CFD of
 ,
i.e.
,
i.e.
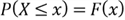 ,
then
,
then
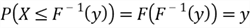
- From steps 5 and 6, we have known:
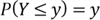
- The CDF
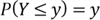 describes distribution
describes distribution
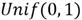 ,
therefore we proved the second part of the theorem;
,
therefore we proved the second part of the theorem;
The proof helps to strengthen our understanding of the theorem. In the rest of this tip, we will demonstrate a method to generate random variables from specified distributions. The method can be summarized into 4 steps:
- Derive the inverse function
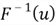 of a specified CDF
of a specified CDF
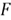 ;
;
- Produce a random number from the standard uniform distribution,
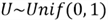 ;
;
- Plug the random number into the inverse function
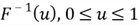 ;
;
- Return generated random number
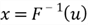 ,
which has the CDF
,
which has the CDF
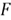 ;
;
4.2 Discrete Random Number Generator
The inverse function of the CDF for a discrete function is discontinuous. Assuming
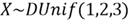 ,
the CDF is given by
,
the CDF is given by
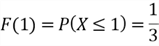
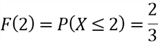
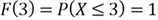
Figure 3 illustrates the CDF for the discrete function. The point (2, 0.6) implicates
how we define the inverse function: given
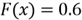 ,
we then find
,
we then find
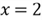 .
By defining
.
By defining
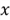 in terms of CDF, we obtained the inverse function in the following equation. This
expression demonstrates a simple search algorithm.
in terms of CDF, we obtained the inverse function in the following equation. This
expression demonstrates a simple search algorithm.
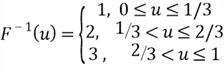
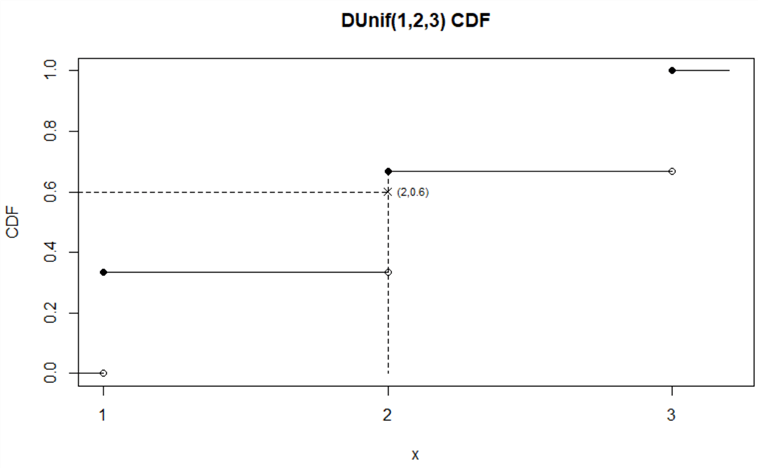
Figure 3 The Cumulative Distribution Function for
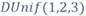
4.2.1 Generating a Random Number from the Discrete Uniform Distribution
Let’s revisit the example: generating a completely random integer number in the range [1,3].
Step 1. Derive the inverse function
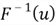 of the CDF
of the CDF
 .
We have already derived the inverse function:
.
We have already derived the inverse function:
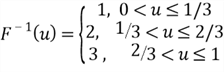
Step 2. Produce a random number from
 .
We use the following SQL statement to generate a random value:
.
We use the following SQL statement to generate a random value:
SELECT RAND(CHECKSUM(NEWID())) AS Random_Number
The query returned a random number: 0.351873119639275. If you run this query, you would obtain a different value from mine.
Step 3. Plug the value,
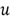 = 0.351873119639275, into the inverse function
= 0.351873119639275, into the inverse function
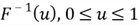 :
:
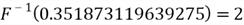
Step 4. Return the generated random number
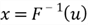 .
The random number generator returns
.
The random number generator returns
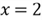 .
.
I wrote a script to examine whether the random numbers generated are distributed
as
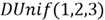 .
In the script, I ran this 4-steps procedure 10,000 times, then loaded the results
into a data frame in R. I plotted a bar chart of frequency distribution to visualize
the probability of choosing each integer in the set {1, 2, 3}.
.
In the script, I ran this 4-steps procedure 10,000 times, then loaded the results
into a data frame in R. I plotted a bar chart of frequency distribution to visualize
the probability of choosing each integer in the set {1, 2, 3}.
# Reset the compute context to your local workstation.
rxSetComputeContext("local")
# Define connection string to SQL Server
sql.server.conn.string <- "Driver=SQL Server;Server=.;Database=TutorialDB;Trusted_Connection={Yes}"
# Create an RxSqlServerData data source object
data.source.object <- RxSqlServerData(sqlQuery = "
SELECT top 10000
x.random_value,
CASE
WHEN x.random_value <= (1.0/3.0) THEN 1
WHEN x.random_value > (1.0/3.0) and x.random_value <= (2.0/3.0) THEN 2
WHEN x.random_value > (2.0/3.0) and x.random_value <= 1.0 THEN 3
END as random_integer
FROM sys.all_columns a1
CROSS APPLY sys.all_columns a2
CROSS APPLY
(
SELECT RAND(CHECKSUM(NEWID())) as random_value
) x
",
connectionString = sql.server.conn.string)
# Read the data into a data frame in the local R session.
data.frame.random.numbers <- rxImport(data.source.object)
# Create a Frequency Distribution Bar Chart quickly with the plot() function
# when the categorical variable to be plotted is a factor or ordered factor.
plot(as.factor(data.frame.random.numbers$random_integer), main = "Frequency Distribution of Random Integers",
xlab = "Random Integer",
ylab = "Number of Occurrence",
col = "blue")
I have obtained a bar chart as shown in Figure 3. Comparing to Figure 1, the chance of selecting one number from these three integer numbers was almost equally likely.
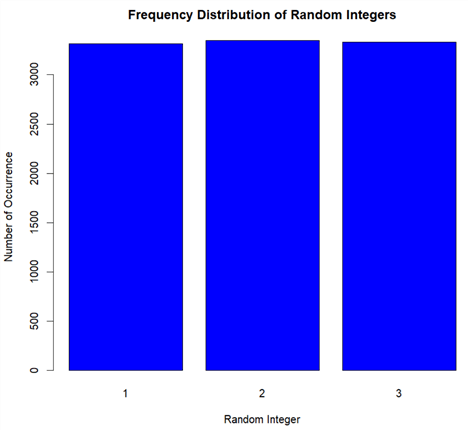
Figure 4 Frequency Distribution of Generated Random Integers
4.2.2 Generating a Random Number from the Bernoulli Distribution
Now let’s look at a case where events are not equally likely to occur.
We are asked to generate sample data from a Bernoulli distribution,
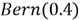 .
.
Step 1. Derive the inverse function
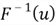 of the CDF
of the CDF
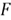 .
The
.
The
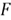 is written as
is written as
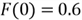
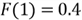
Then, the inverse function of this CDF is given by
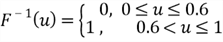
Step 2. Produce a random number from
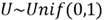 .
We used the following SQL statement to generate a random value, and the query returned
a random number: 0.418275981900669:
.
We used the following SQL statement to generate a random value, and the query returned
a random number: 0.418275981900669:
SELECT RAND(CHECKSUM(NEWID())) AS Random_Number
Step 3. Plug the value,
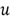 = 0. 418275981900669, into the inverse function
= 0. 418275981900669, into the inverse function
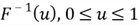 :
:
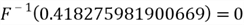
Step 4. Return the generated random number
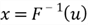 .
The random number generator returns
.
The random number generator returns
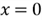 .
.
To verify the generated random numbers are from
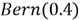 ,
I ran the 4-step procedure 10,000 times through a R script. I plotted a bar chart
of frequency distribution to visualize the chances of generating the number 0 and
1.
,
I ran the 4-step procedure 10,000 times through a R script. I plotted a bar chart
of frequency distribution to visualize the chances of generating the number 0 and
1.
# Reset the compute context to your local workstation.
rxSetComputeContext("local")
# Define connection string to SQL Server
sql.server.conn.string <- "Driver=SQL Server;Server=.;Database=TutorialDB;Trusted_Connection={Yes}"
# Create an RxSqlServerData data source object
data.source.object <- RxSqlServerData(sqlQuery = "
SELECT top 10000
x.random_value,
CASE
WHEN x.random_value <= 0.6 THEN 0
WHEN x.random_value > 0.6 and x.random_value <= 1.0 THEN 1
END as random_integer
FROM sys.all_columns a1
CROSS APPLY sys.all_columns a2
CROSS APPLY
(
SELECT RAND(CHECKSUM(NEWID())) as random_value
) x
",
connectionString = sql.server.conn.string)
# Read the data into a data frame in the local R session.
data.frame.random.numbers <- rxImport(data.source.object)
# Create a Frequency Distribution Bar Chart quickly with the plot() function
# when the categorical variable to be plotted is a factor or ordered factor.
plot(as.factor(data.frame.random.numbers$random_integer), main = "Frequency Distribution of Random Integers",
xlab = "Random Integer",
ylab = "Number of Occurrence",
col = "blue")
The bar chart, shown in Figure 5, illustrates that the chance of success, i.e.
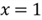 ,
is 40%, and the chance of failure, i.e.
,
is 40%, and the chance of failure, i.e.
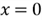 ,
is 60%. The sample data has the desired distribution.
,
is 60%. The sample data has the desired distribution.
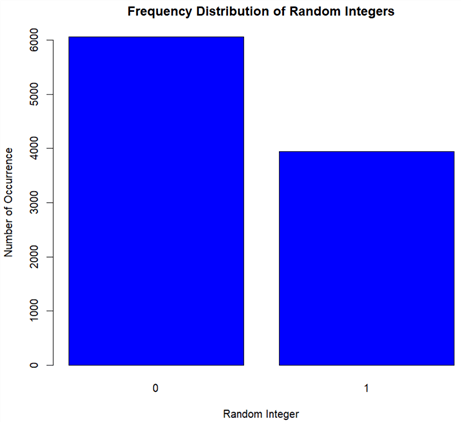
Figure 5 Frequency Distribution of Generated Random Integers
4.2.3 Generating a Random Number from the Binomial Distribution
Deriving an inverse function
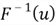 of a CDF
of a CDF
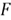 is the critical step in this 4-step process. Sometimes, it may be difficult to find
the inverse function of a CDF. This section introduces a search algorithm to find
the value of random variable
is the critical step in this 4-step process. Sometimes, it may be difficult to find
the inverse function of a CDF. This section introduces a search algorithm to find
the value of random variable
 when given a value of CDF.
when given a value of CDF.
Assuming
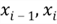 are in the support of
are in the support of
 ,
and they are in an ascending order. Because the CDF
,
and they are in an ascending order. Because the CDF
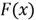 is an increasing function, this inequality exists:
is an increasing function, this inequality exists:
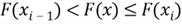
Through the method of computing CDF from PMF, the above inequality can be written as:
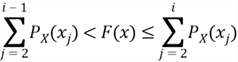
Then, given PMF, we can find the value of
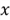 that makes
that makes
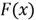 satisfy the inequality.
satisfy the inequality.
Let’s look at the grocery store example in the section 2.3. To simplify the calculation, we use the data in Table 2.
Step 1. Derive the inverse function
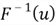 .
Inspired by
Matt’s article [11], I wrote a Pseudo-code to explain how to numerically
compute the returning values of the inverse function:
.
Inspired by
Matt’s article [11], I wrote a Pseudo-code to explain how to numerically
compute the returning values of the inverse function:
Input: the lookup value "u", a list of PMF values "probability list", a list of sequential random numbers "random number list". //Each element in the probability list corresponds the element in the random list.
Output: the value of random variable.
discrete inverse function ("u", "probability list", "random number list")
{
FOR each position number in the probability list
IF the position number is 1 THEN
Do Nothing
ELSE
F1 = sum of values in the probability list from 1 to the position number less 1
F2 = sum of values in the probability list from 1 to the position number
IF (the value of "u" is greater than F1)
and (the value of "u" is less than or equal to F2) THEN
REUTN the element in the random number list based on the position
END IF
END IF
END FOR
}
Step 2. Generate a random number from
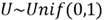 .
We used the following SQL statement to generate a random value and the query returned
a random number: 0.782271114545155:
.
We used the following SQL statement to generate a random value and the query returned
a random number: 0.782271114545155:
SELECT RAND(CHECKSUM(NEWID())) AS Random_Number
Step 3. Plug the value,
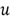 =
0.782271114545155, into the inverse function
=
0.782271114545155, into the inverse function
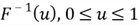 :
:
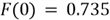
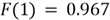
Since
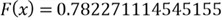 ,
we have
,
we have
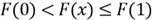
The approach to find the returning value of the inverse function is analogous to Figure 3, thus
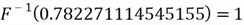
Step 4. Return the generated random number
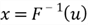 .
The random number generator returns
.
The random number generator returns
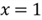 .
.
I wrote a SQL script to run the 4-step procedure 10,000 times, then computed the mean and variance of these generated numbers.
USE TutorialDB GO CREATE TABLE #generated_random_numbers ( random_numbernumeric(16,14) ); GO DECLARE @random_value TABLE ( posint, kint, pnumeric(16,14) ) DECLARE @random_list_size int = 7, @look_count int = 2, @unif numeric(16,14) = RAND(CHECKSUM(NEWID())), @rtn_random_value int = 0 insert into @random_value values (1, 0,0.7350919), (2,1,0.2321343), (3,2,0.03054398), (4,3,0.002143437), (5,4,8.460938e-05), (6,5,1.78125e-06), (7,6,1.5625e-08) WHILE @look_count <= @random_list_size BEGIN IF (@unif > (SELECT SUM(p) FROM @random_value WHERE pos <= @look_count -1) AND @unif <= (SELECT SUM(p) FROM @random_value WHERE pos <= @look_count)) SELECT @rtn_random_value = k FROM @random_value WHERE pos <= @look_count SET @look_count = @look_count + 1 END INSERT INTO #generated_random_numbers VALUES(@rtn_random_value) GO 10000 SELECT COUNT(*)AS [Sample Size], AVG(random_number)AS [Expectation], VAR(random_number)AS [Variance] FROM #generated_random_numbers GO SELECT CAST(random_number as INT)AS [Random Number], COUNT(*)*1.0/10000.0AS[Relative Frequency] FROM #generated_random_numbers GROUP BY random_number ORDER BY random_number GO DROP TABLE #generated_random_numbers; GO
In theory, the expectation and variance of binomial distribution
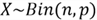 are given by
are given by
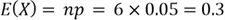
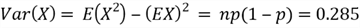
Comparing the statistics of the generated numbers, shown in Figure 6, to the
theoretical computation results, they are close. The relative frequency table in
Figure 6 does not include random numbers 4, 5 and 6. The probabilities to produce
these numbers are very low. We need to increase the sample size in order to generate
all possible values. The results in Figure 6 indicate that the sample data approximately
has
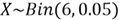 .
.
Figure 6 The Screenshot of Sample Statistics Calculated by T-SQL
4.3 Continuous Random Number Generator
We have given some practice in use of the universality of the uniform theorem to generate discrete variables from specific distributions. The critical step is to derive an inverse or near-inverse function of CDF. When the CDF of a continuous variable is invertible, we continue to use the 4-step method. Tim [12] provides a list of inverse functions of CDFs. We must consider other approaches when we cannot express the inverse function by using the standard elementary functions. In this section, we first walkthrough an example when the inverse function of CDF exists, then we generate a random variable from a distribution without a closed-form inverse function of the CDF.
4.3.1 Generating a Random Number from the Uniform Distribution
We are going to generate test data from
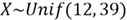 .
the CDF is given by
.
the CDF is given by
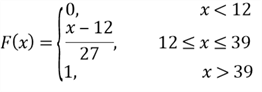
Step 1. Derive the inverse function
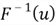 of the CDF
of the CDF
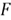 :
:
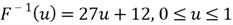
Step 2. Produce a random number from
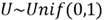 .
We used the following SQL statement to generate a random value and the query returned
a random number: 0.220432802523734:
.
We used the following SQL statement to generate a random value and the query returned
a random number: 0.220432802523734:
SELECT RAND(CHECKSUM(NEWID())) AS Random_Number
Step 3. Plug the value,
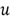 =
0.220432802523734, into the inverse function
=
0.220432802523734, into the inverse function
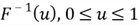 :
:
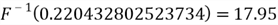
Step 4. Return the generated random number
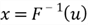 .
The random number generator returns
.
The random number generator returns
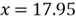 .
.
To examine the generated random numbers are from
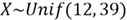 ,
I wrote a script to execute the 4-step procedure 10,000 times, then loaded the results
into a data frame in R. I plotted a histogram to illustrate the frequency distribution.
,
I wrote a script to execute the 4-step procedure 10,000 times, then loaded the results
into a data frame in R. I plotted a histogram to illustrate the frequency distribution.
# Reset the compute context to your local workstation.
rxSetComputeContext("local")
# Define connection string to SQL Server
sql.server.conn.string <- "Driver=SQL Server;Server=.;Database=TutorialDB;Trusted_Connection={Yes}"
# Create an RxSqlServerData data source object
data.source.object <- RxSqlServerData(sqlQuery = "
SELECT top 10000
x.random_value,
x.random_value * 27.0 + 12.0 as random_number
FROM sys.all_columns a1
CROSS APPLY sys.all_columns a2
CROSS APPLY
(
SELECT RAND(CHECKSUM(NEWID())) as random_value
) x
",
connectionString = sql.server.conn.string)
# Read the data into a data frame in the local R session.
data.frame.random.numbers <- rxImport(data.source.object)
# Create a Histogram of Random Numbers
hist(data.frame.random.numbers$random_number, main = "The Histogram of Random Numbers",
breaks = seq(12,39,by=3),
xlab = "Random Number",
ylab = "Frequency",
col = "blue")
Figure 7 indicates that these random numbers are approximately uniformly distributed in the range [12, 27].
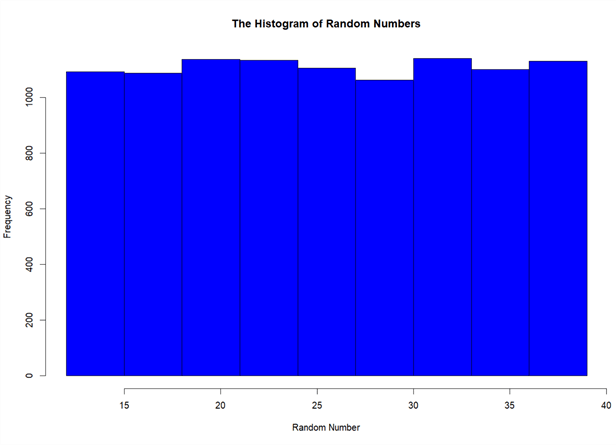
Figure 7 The Histogram of Random Numbers
4.3.2 Generating a Random Number from the Standard Normal Distribution
The standard normal distribution, denoted by
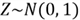 ,
is widely used probability distribution. Both PDF and CDF, given in the section
3.2, are not closed-form expression. We are going to use the Box-Muller transformation
[13] for generating a standard normal variable:
,
is widely used probability distribution. Both PDF and CDF, given in the section
3.2, are not closed-form expression. We are going to use the Box-Muller transformation
[13] for generating a standard normal variable:
- Generate two continuous random variables from the standard uniform distribution:
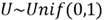 and
and
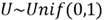 ;
;
- Create two functions of these two standard uniform random variables:
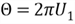
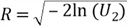
- Obtain two identically independent standard normal distributions:
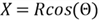
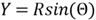
Several approaches [14,15] have proven the Box-Muller transformation. I prefer to the explanation in chapter 8 of book [4], which is easier to understand.
I have run a script to examine these random numbers generating from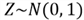 .
The script ran these 3 steps 10,000 times. I plotted a histogram to illustrate the
frequency distribution of these random numbers.
.
The script ran these 3 steps 10,000 times. I plotted a histogram to illustrate the
frequency distribution of these random numbers.
# Reset the compute context to your local workstation.
rxSetComputeContext("local")
# Define connection string to SQL Server
sql.server.conn.string <- "Driver=SQL Server;Server=.;Database=TutorialDB;Trusted_Connection={Yes}"
# Create an RxSqlServerData data source object
data.source.object <- RxSqlServerData(sqlQuery = "
SELECT top 10000
sqrt(-2.0*log(random_value_2))*cos(2.0*pi()*(random_value_1)) as random_number_x,
sqrt(-2.0*log(random_value_2))*sin(2.0*pi()*(random_value_1)) as random_number_y
FROM sys.all_columns a1
CROSS APPLY sys.all_columns a2
CROSS APPLY
(
SELECT RAND(CHECKSUM(NEWID())) as random_value_1,
RAND(CHECKSUM(NEWID())) as random_value_2
) x
",
connectionString = sql.server.conn.string)
# Read the data into a data frame in the local R session.
data.frame.random.numbers <- rxImport(data.source.object)
# Create a a standard normal distribution
densitySamps <- seq(-4, 4, by = 0.01)
# 2 figures arranged in 1 row and 2 columns
par(mfrow = c(1, 2))
# Create a Histogram of Random Numbers
hist(data.frame.random.numbers$random_number_x, main = "The Histogram of Random Variable X",
xlab = "X",freq = FALSE)
# Add a standard normal density curve
lines(densitySamps, dnorm(densitySamps), lwd = 2, col = "red")
# Create a Histogram of Random Numbers
hist(data.frame.random.numbers$random_number_y, main = "The Histogram of Random Variable Y",
xlab = "Y", freq = FALSE)
# Add a standard normal density curve
lines(densitySamps, dnorm(densitySamps), lwd = 2, col = "red")
Figure 8 illustrates that the random variables approximately have the standard normal distribution.
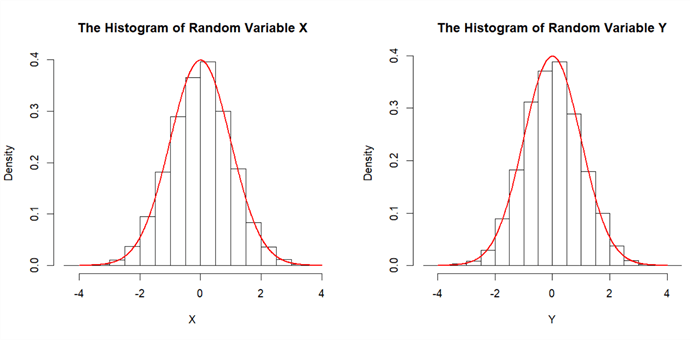
Figure 8 The Histograms of two Random Variables X and Y
Summary
In this tip, we have explored random variables and their distributions. We have learned the universality of the uniform theorem, and Box-Muller transformation, as well as how to create random values from a specific distribution. We used R language to execute SQL statements for generating random numbers and applied visualization techniques to examine frequency distributions of these random numbers.
The universality of the uniform theorem has been proved in this tip so that the 4-step method was provided to generate a random variable from any specific distribution. We also demonstrated numerical methods to find inverse functions of cumulative distribution functions.
References
[1] Snider, D. (2016, March 29). SQL Server T-SQL Code to Generate a Normal Distribution. Retrieved from https://www.mssqltips.com/sqlservertip/4233/sql-server-tsql-code-to-generate-a-normal-distribution/.
[2] Snider, D. (2014, August 04). Create Your Own RANDBETWEEN Function in T-SQL. Retrieved from https://www.mssqltips.com/sqlservertip/3297/create-your-own-randbetween-function-in-tsql/.
[3] Camps, D. (2012, July 03). Generating Non-uniform Random Numbers with SQL. Retrieved from https://www.sqlservercentral.com/articles/generating-non-uniform-random-numbers-with-sql/.
[4] Blitzstein, K. J. & Hwang, J. (2015). Introduction to Probability. Boca Raton, FL: CRC Press.
[5] Jost, S. (2017). CSC 423: Data Analysis and Regression. Retrieved from DePaul University Website: http://facweb.cs.depaul.edu/sjost/csc423/
[6] Collins online dictionary. Random. Retrieved from https://www.collinsdictionary.com/dictionary/english/random.
[7] Collins online dictionary. Variable. Retrieved from https://www.collinsdictionary.com/dictionary/english/variable.
[8] Downey, B. A. (2014, October). Think Stats, 2nd Edition. Sebastopol, CA: O’Reilly Media.
[9] Guttman, I., & Gupta, C. B. (2013). Statistics and Probability with Applications for Engineers and Scientists. Hoboken, NJ: John Wiley & Sons.
[10] Stewart, J. W. (2009). Probability, Markov Chains, Queues, and Simulation. Princeton, NJ: Princeton University Press.
[11] Bonakdarpour, M. (2016, February 02). Inverse Transform Sampling. Retrieved from fiveMinuteStats: https://stephens999.github.io/fiveMinuteStats/inverse_transform_sampling.html/.
[12] Hargreaves, T. (2019, February). Generating Normal Random Variables - Part 1: Inverse Transform Sampling. Retrieved from T-Tested: https://www.ttested.com/generating-normal-random-variables-part-1/.
[13] Box, G. E. P.& Muller, Mervin E. (1958). A Note on the Generation of Random Normal Deviates. Ann. Math. Statist. 29 (1958), no. 2, 610--611. doi:10.1214/aoms/1177706645. https://projecteuclid.org/euclid.aoms/1177706645
[14] Goodman, J. (2005, August). Chapter 2: Simple Sampling of Gaussians. Retrieved from Courant Institute: https://www.math.nyu.edu/faculty/goodman/teaching/MonteCarlo2005/notes/GaussianSampling.pdf.
[15] Vafa, K. (2017, February). The Box-Muller Transform. Retrieved from keyonvafa.com: http://keyonvafa.com/box-muller-transform/.
Next Steps
- Many Q&As on the web have covered random value generation. Some methods may not generate completely random numbers, although they many do produce random numbers. We can use knowledge of probability to verify these random variables distributions. However, this tip is only an introduction to probability, and there is still more to learn if you wish to develop data analysis skills. I strongly recommend the course: Statistics 110: Probability, which has been taught at Harvard University by Professor Joe Blitzstein. More information about this course are available on the course site: https://projects.iq.harvard.edu/stat110.
- Check out these related tips:
About the author
 Nai Biao Zhou is a Senior Software Developer with 20+ years of experience in software development, specializing in Data Warehousing, Business Intelligence, Data Mining and solution architecture design.
Nai Biao Zhou is a Senior Software Developer with 20+ years of experience in software development, specializing in Data Warehousing, Business Intelligence, Data Mining and solution architecture design.This author pledges the content of this article is based on professional experience and not AI generated.
View all my tips