Getting Started with Statistics using Python

By: Hristo Hristov   |   Updated: 2022-05-03   |   Comments (2)   |   Related: > Python

Problem

In your work as a data analyst, you may frequently be up against heaps of numerical data. A typical first step in making sense of a large data set is calculating some descriptive statistics, such as the mean, median, mode, variance and standard deviation, among others. With these measures at hand we can proceed further to more complex data analysis.

Solution

This tutorial proposes several ways to describe your data by using pure Python programming language with no additional libraries used. This tutorial has one goal: show Python in action in the statistics context. It is fair to say in your daily work you will probably use libraries such as numpy, pandas or scipy instead of building the code yourself. Here though you can see the internal workings of the functions. That said, let us begin with the mean.

Mean

Consider the following sample data where we have a list of integers (could also be a float data type) and we wanted to calculate the mean. The mean of a sequence of numbers is the sum of the numbers divided by the length of the sequence:

numbers = [4,10,29,33,42,67]
def find_mean(list_of_numbers):
     sum_n = sum(list_of_numbers)
     len_n = len(list_of_numbers)
     mean = sum_n/len_n
     return mean
    
result = find_mean(numbers)

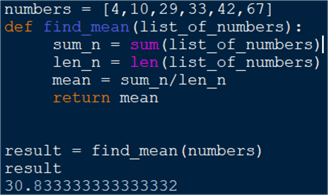
We define a function that accepts a single parameter which is a list of numbers. The function definition contains:

• variable sum_n using the sum function to sum up all members of the list
• variable len_n using the len function to get the length of the sequence
• and a variable for the result: mean, which is by the definition dividing the sum by the length.

In this case the result is 30.83. Notice the function sum accepts any iterable so you could easily directly pass a tuple or a set to it instead of a list. Len on the other hand, accepts any object and counts the number of items contained within.

Median

The median is another type of average which tells us what the middle value of a dataset is.

To find it, we must arrange the sequence of numbers in ascending order. The way the median is calculated depends on if the sequence contains an even or an odd number of elements. Therefore, we need to account for both cases:

numbers_even = [4,10,29,33,42,67] # 6 elements
numbers_odd = [4,10,29,33,42,67,99] # 7 elements
def find_median(list_of_numbers):
    list_of_numbers.sort()
    length = len(list_of_numbers)
    length_is_odd = True if length % 2 == 0 else False
    if length_is_odd:
        index = length//2
        median = list_of_numbers[index]
    else:
        index_1 = length//2
        index_2 = index_1 + 1
        median = (list_of_numbers[index_1] + list_of_numbers[index_2]) / 2
    return median
 
find_median(numbers_odd)
find_median(numbers_even)

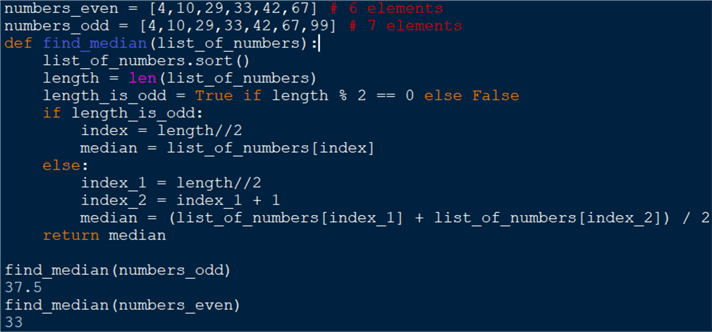
If an odd number of elements is present, then the median is the middle value, which is easy to spot. If there are even numbers, we must sum up the middle two values. Their mean is the median of the sequence. So, the function definition consists of:

• Sorting the sequence using sort(). This function works in place, overwriting the current object, therefore we do not need an extra variable to hold the sorted sequence.
• Taking the length of the sequence using len()
• Defining a Boolean variable length_is_odd checking if the input sequence has an odd or even number of elements
• Branching out the function definition according to the length_is_odd variable:
  • If true, we just do an integer division of the sequence length by 2 (denoted by double /). This action performs integer division and automatically returns an integer. Then we pass the result as an index to our input sequence and get the median
  • If false, the length is an even number. We must take the middle two members. We do so by another integer division to take the "left" index and assigning to index_1. By adding 1 to that result, we get index_2 denoting the "right" index. Finally, we take the mean of the two values which is the median of the sequence of even numbers.

We could even use our previous function for calculating the mean. However, the code may become a bit more verbose as we need an extra sequence variable to hold the numbers at index 1 and 2:

# continued 
middle_numbers = []
middle_numbers.append[list_of_numbers[index_1]]
middle_numbers.append[list_of_numbers[index_2]]
median = find_mean(middle_numbers)

Mode

The mode of a sequence is the number occurring most frequently.

To implement this, we must construct an algorithm consisting of two steps:

1. Count the occurrences of each number in the sequence
2. Take the number with the highest occurrence.

Here is an example:

n = [4,4,4,4,6,6,6,6,6,6,8,8,8,8,9,10,2,2,2,2,2,2,2,2,2,2]
def calculate_mode(list_of_numbers):
    counter = {}
    for i in list_of_numbers:
        if i in counter:
            counter[i]+=1
        else:
            counter[i] = 1
    key_max = sorted(counter, key=counter.get, reverse=True)[:1][0]
    frequency = counter[key_max]
    return key_max, frequency
 
calculate_mode(n)

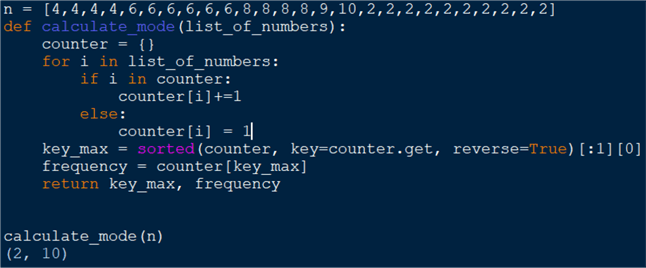
Here we have a list of numbers n. All elements are present more than once and we must find out which element has the highest frequency. In the calculate_mode function we start by instantiating an empty dictionary counter. For every element of the input sequence, we check if the number is already a key in that dictionary. If so, we increment the count by one. If not, we create the key. Then, we sort the dictionary with the sorted function in reverse order and take the first element by slicing (slicing by index [:1] is non inclusive, thus taking the first element only). However, the key is a one-element list so we must add [0] to ensure grabbing the only integer value contained. From there it is easy to return the key and the corresponding value which is the frequency of the number in the input sequence. In this case the mode is 2 appearing 10 times.

Note: previously we have used the sort() function. Here we cannot use it because it is applicable only to lists. The function we can use to sort the dictionary is sorted which returns a copy of the object being sorted.

Min, max and range

Another description you may want to produce for your data set is the minimum and maximum values and the range (the difference between the min and the max).

Here we have a very small data set, but for a much bigger one, the min, max and range may be impossible to spot without using a dedicated function for that. For example:

numbers = [4,10,29,33,42,-67]
def find_range(list_of_numbers):
    n_min = min(list_of_numbers)
    n_max = max(list_of_numbers)
    n_range = n_max - n_min
    return n_min, n_max, n_range
find_range(numbers)
(-67, 42, 109)

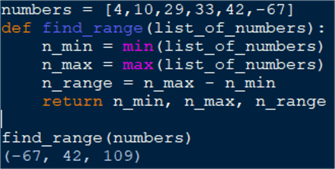
This is straightforward: we use the built-in min and max functions accordingly. To get the range we subtract the min from the max. Finally, we return a tuple of the results. If you assign the function output to a variable you will be able to access each value by its index, [0] being the minimum for the argument dataset.

Variance and standard deviation

Both variance and standard deviation (STDev) represent measures of dispersion, i.e., how far from the mean the individual numbers are.

For example, a low variance means most of the numbers are concentrated close to the mean, whereas a higher variance means the numbers are more dispersed and far from the mean. There is a caveat here: calculating the variance correctly depends on if we are working with a sample of data or with the whole population. Our function needs to account for that:

def find_variance(list_of_numbers, var_type):
    # argument check
    valid_var_types = ['sample', 'population']
    if var_type not in valid_var_types:
        raise ValueError(f'Incorrect argument for variance type passed: {var_type}! Allowed values \'sample\' or \'population\'')
    # define correct sequence length        
    seq_length = len(list_of_numbers)-1 if var_type == 'sample' else len(list_of_numbers)
    # using the previously defined function
    mean = find_mean(list_of_numbers) 
    # find differences and squared differences
    differences = [number-mean for number in list_of_numbers]
    squared_differences = [x**2 for x in differences]
    # calculate
    variance = sum(squared_differences)/seq_length
    std = variance ** 0.5
    return round(variance, 2), round(std, 2)
 
numbers = [4,10,29,33,42,67]
find_variance(numbers, 'sample')
find_variance(numbers, 'population')
find_variance(numbers, 'pop')

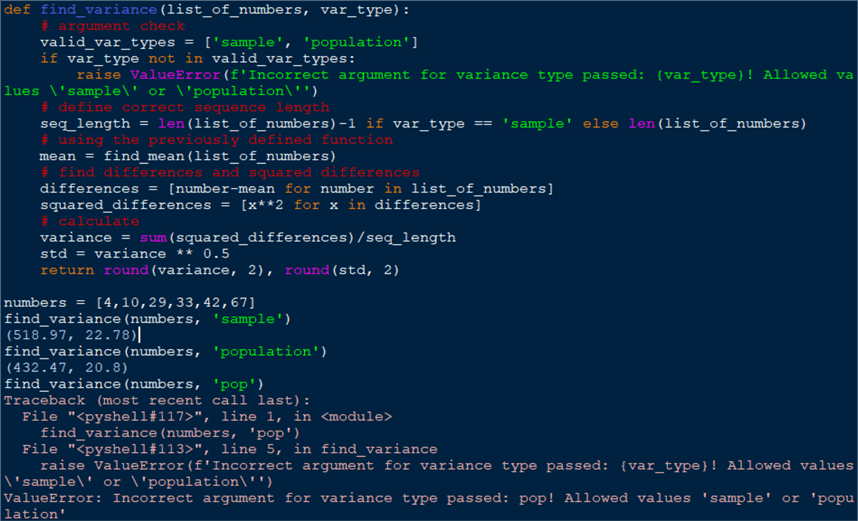
The function definition begins by defining a list of the valid "variance types" we can accept as arguments: sample or population. If another argument is passed, the function will raise a ValueError. Then we have the variable seq_length. If we are working with a sample, then we take the length of the sequence – 1. If we are working with a population, then we take the length as is. Next, we calculate the mean by using the function we have already defined. According to the definition of the variance in statistics, the next thing is to make a list of the differences between each element in the sequence and the mean. Having this list differences, we then need to square each of those values and store it in the squared_differences list. Notice the use of list comprehension which comes in handy, instead of using a for loop. Finally, we calculate the variance by summing up the values in the squared differences list and dividing by the respective length. For some readability, we can round the result up and return a tuple of the variance and the standard deviation. We can test the function with two calls with the same sequence. In the first case we represent a sample, while in the second a population.

Correlation

The correlation coefficient, typically referring to Pearson's, is a measure of dependence between two sets of data.

Here we will construct a Python function from scratch for calculating the correlation coefficient according to the formula for a sample:

def find_correlation(x,y):
    length = len(x)
    # sum of products
    products = [x_i*y_i for x_i, y_i in zip(x,y)]
    sum_products = sum(products)
    sum_x = sum(x)
    sum_y = sum(y)
    squared_sum_x = sum_x**2
    squared_sum_y = sum_y**2
    # x squared and sum
    x_sq = [x_i**2 for x_i in x]
    x_sq_sum = sum(x_sq)
    #y squared and sum
    y_sq = [y_i**2 for y_i in y]
    y_sq_sum = sum(y_sq)
    # calculate correlation according to the formula
    numerator = length*sum_products - sum_x*sum_y
    denominator_term1 = length*x_sq_sum - squared_sum_x
    denominator_term2 = length*y_sq_sum - squared_sum_y
    denominator = (denominator_term1*denominator_term2)**0.5
    corr = numerator/denominator
    return corr

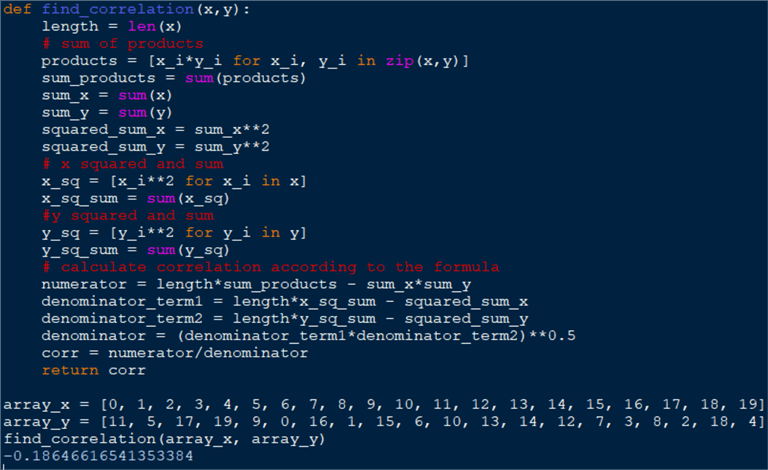
The function definition begins by taking the length of the sequence x. The assumption is x and y are of the same length. A more secure way to do it would be to check the length first and take the one of the shorter sequence if the two are different. After that, we multiply each element from x with each element in y and assign the result to the products variable. We sum the elements of x and y and calculate the square of each sum according to the definition for finding a correlation, resulting in the variables sum_x, sum_y, squared_sum_x and squared_sum_y. Next, for each input sequence we square the contained element and sum the result. The variables are x_sqand x_sq_sum for x and y_sq and y_sq_sum for y. In the last block of code, we construct the numerator and denominator terms according to the statistical formula for correlation. The result is calculated by dividing the numerator by the denominator.

To double-check our function, we can resort to the scipy package where we have a built-in pearsonr function:

As we see the result is essentially the same.

Conclusion

In this tutorial we examined how to develop from scratch functions for calculating the mean, median, mode, max, min range, variance, and standard deviation of a data set. Additionally, we investigated how to find the correlation between two datasets. With these examples, I hope you will have a better understanding of using Python for statistics.

Next Steps

• Measures of central tendency
• Measures of dispersion
• Pearson Correlation Coefficient (PCC)
• Linear Regression with Python in SQL Server
• Learn Python with me
  • Define and call functions in Python
  • Python list comprehension

About the author

Hristo Hristov is a Data Scientist and Power Platform engineer with more than 12 years of experience. Between 2009 and 2016 he was a web engineering consultant working on projects for local and international clients. Since 2017, he has been working for Atlas Copco Airpower in Flanders, Belgium where he has tackled successfully multiple end-to-end digital transformation challenges. His focus is delivering advanced solutions in the analytics domain with predominantly Azure cloud technologies and Python. Hristo's real passion is predictive analytics and statistical analysis. He holds a masters degree in Data Science and multiple Microsoft certifications covering SQL Server, Power BI, Azure Data Factory and related technologies.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips