By: John Miner | Updated: 2024-03-19 | Comments | Related: 1 | 2 | 3 | 4 | 5 | > Apache Spark
Problem
There are two ways in which a big data engineer can transform files: Spark dataframe methods or Spark SQL functions. I like the Spark SQL syntax since it is more popular than dataframe methods. Every language has at least three core data types: strings, numbers, and date/time. How do we manipulate numbers using Spark SQL?
Solution
The previous tip reviewed the syntax for date/time Spark SQL functions. This tip will focus on learning the available numeric functions.
Spark SQL has so many numeric functions that they must be divided into three categories: basic, binary, and statistical. Today, we will discuss what I consider basic functions that are seen in most databases and/or languages.
Business Problem
Our manager has asked us to explore the syntax of the numeric functions available in Azure Databricks. In my examples, I will execute Spark SQL using the magic command in a Python notebook. This is how I test my SQL syntax before embedding it in a spark.sql call. At the end of this article, big data engineers will have a good overview of numeric functions.
Basic Arithmetic
The Spark ecosystem has evolved since its creation in 2012. The engine is written in Scala, but the library (PySpark) used in the examples is in Python. Therefore, it is not surprising that some functions return the same result but are named differently. In this section, I will cover what is known as operators in a given programming language.
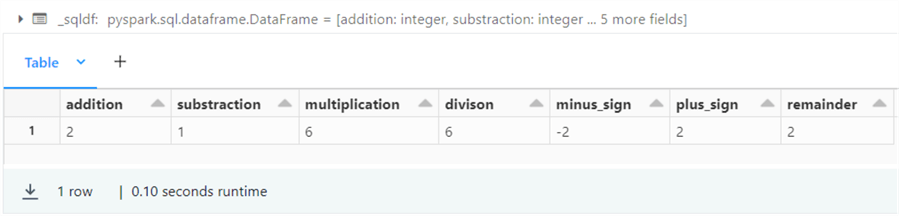
%sql -- -- 1 - Basic Arithmetic -- select 1 + 1 as addition, 2 - 1 as subtraction, 2 * 3 as multiplication, 18 / 3 as division, - 2 as minus_sign, + 2 as plus_sign, 20 % 3 as remainder;
The above code snippet performs some random arithmetic. Please see the table below, which has links to the functions explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | + | Addition operator |
| 2 | - | Subtraction operator |
| 3 | * | Multiplication operator |
| 4 | / | Division operator |
| 5 | % | Remainder operator |
| 6 | + | Positive operator |
| 7 | - | Negative operator |
The output below shows the results of executing the Spark SQL query. I chose to use whole numbers (integers) as the data type. However, the same functionality is available for real numbers (floating point).
This use case was kind of simple. Let's imagine a customer is looking to build a house with 10,000 square feet of space using the following geometric shapes. What might be the dimensions of each house?
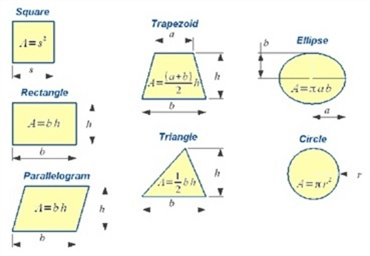
The code snippet below has sample house sizes for each shape. The total square footage must be 10,000.
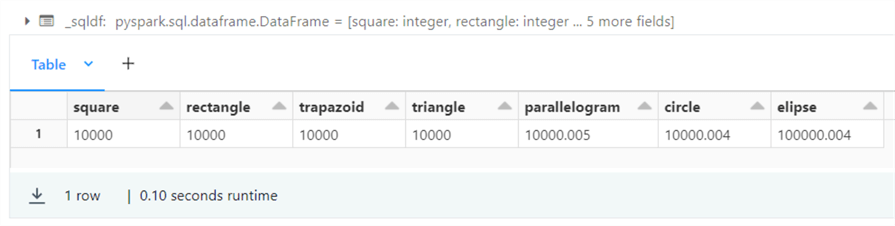
%sql -- -- 2 – Simple geometry problems -- select 100 * 100 as square, 40 * 250 as rectangle, (75 + 125) / 2 * 100 as trapazoid, (200 * 100) / 2 as triangle, round(75 * 133.3334, 3) as parallelogram, round(pi() * 3183.1, 3) as circle, round(pi() * 318.3099 * 100, 3) as ellipse;
The output below shows the results of executing the Spark SQL query. Did you notice the ellipse is off by a factor of 10? Please adjust the dimensions to obtain the correct square footage.
Basic Comparisons
Comparing two numbers is part of human nature. For instance, my Ford Ranger has six cylinders, and your Dodge Ram has eight cylinders. Obviously, you have a bigger engine in your truck. The code below explores operators: less than, greater than, less than or equal to, and greater than or equal to. Interestingly, the equals and not equals operators have several forms.
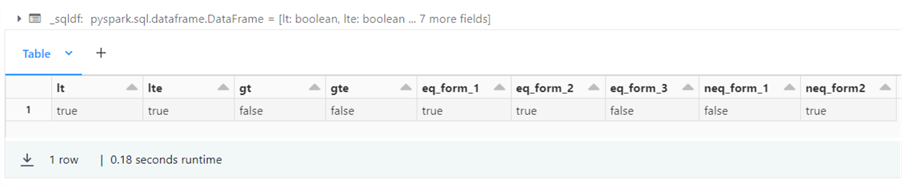
%sql -- -- 3 – numeric comparison -> boolean results -- select 1.5 < 2 as lt, 2 <= 2 as lte, 2 > 3 as gt, 2 >= 3 as gte, 4 = 4 as eq_form_1, 5 == 5 as eq_form_2, Null <=> 1 as eq_form_3, 6 != 6 as neq_form_1, 7 <> 8 as neq_form2;
Please see the table below that has links to the operators explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | < | Less than operator. |
| 2 | <= | Less than or equal to operator. |
| 3 | > | Greater than operator. |
| 4 | >= | Greater than or equal to operator. |
| 5 | = | Equals form 1. |
| 6 | == | Equals form 2. |
| 7 | <=> | Equals form 3 |
| 8 | != | Not equals form 1. |
| 9 | <> | Not equals form 2. |
The output below shows the results of executing the Spark SQL query for testing comparison operators.
While operators are not that interesting, they are very useful. A simple use case is when the current loan payment number equals the number of payments dictated in the loan setup. This condition indicates that the loan is paid off.
Try Functions
Many languages support a version of the arithmetic operators that have error checking. Thus, overflows caused by division by zero are prevented. The following Spark SQL query uses the try functions supported by Spark SQL.
%sql -- -- 4 - Basic Arithmetic - try statements -- select try_add(1, 1) as addition, try_subtract(1, 3) as subtraction, try_multiply(2, 3) as multiplication, try_divide(18, 3) as division;
The output below shows the results of executing the above Spark SQL query for try functions.
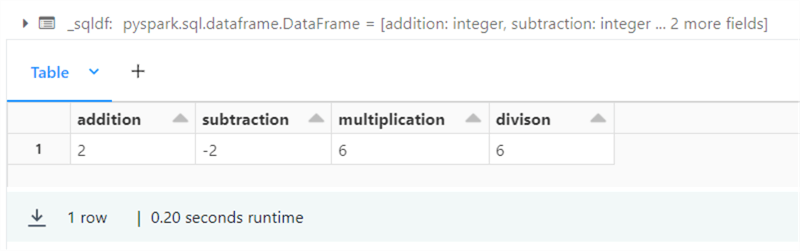
One special try function works on summing up columns in a table. The code below creates a derived table named tab1 with a single column named col1.
%sql -- Try sum function select try_sum(col1) from values (0), (5), (10), (15), (20), (25) as tab1(col1);
The image below shows the output from executing the above Spark SQL query. Remember, any columns that are not named take on the expression as the name.
Please see the table below that has links to the functions that were explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | try_add | Perform addition. |
| 2 | try_subtract | Perform subtraction. |
| 3 | try_multiply | Perform multiplication. |
| 4 | try_divide | Perform division. |
| 5 | try_sum | Sum a given column. |
I do not use the try functions as much as other functions; however, they are available for your use in your Spark SQL queries.
What is Your Sign?
A number is either positive or negative. There are several functions to adjust and/or test a number's sign. The query below explores the boiling point of liquid nitrogen, liquid oxygen, and liquid water in degrees Celsius. Please see this website for these interesting facts.
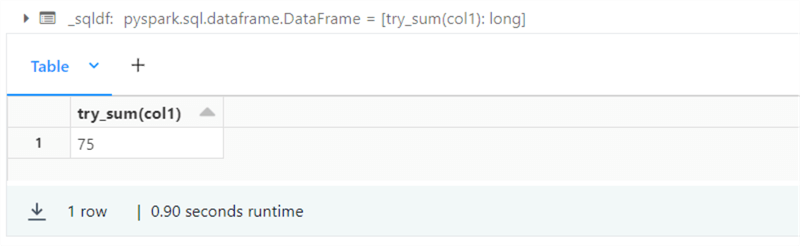
%sql -- -- 5 – about your sign -- select abs(-31) as liquid_nitro, positive(-100) as liquid_h20, negative(183) as liquid_oxygen, sign(100) as positive, sign(-100) as negative, signum(0) as neutral;
The output below shows the results of executing the Spark SQL query for sign functions. The only surprising result is the positive function. It is considered a NOP piece of code, i.e., what goes in comes out. In my opinion, this function should always return the positive of any value. In short, an alias for the abs function.
Please see the table below for links to the sign functions explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | abs | Absolute value. |
| 2 | positive | Just return the value. |
| 3 | negative | Negate the value. |
| 4 | sign | Return negative one, positive one, or zero values. |
| 5 | signum | Returns either -1, 1, or 0 depending upon input. |
Out of all these functions, I use the absolute value the most.
Round vs. Truncate
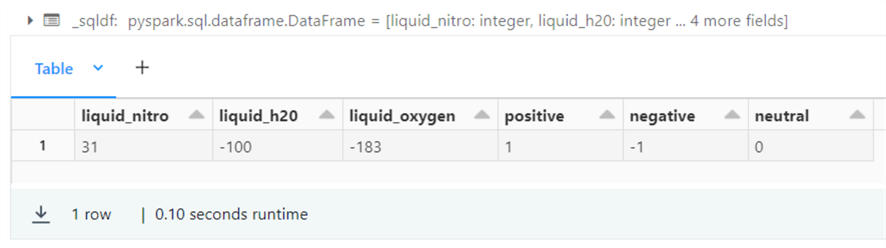
The Spark SQL language contains two rounding functions. The inputs to the function are the candidate number to round and the number of decimals. One uses the half even algorithm and the other uses half up algorithm. Additionally, you might want the next largest integer (ceiling) or the next smallest integer (floor). Another way to define the ceiling function is to calculate the floor and add one to the result. I categorize these two functions as truncate since the decimal part of the number is lost. The example below shows the uses of these functions.
%sql -- -- 6 – round vs truncates -- select round(pi(), 0) as round_zero, bround(pi(), 1) as round_one, bround(pi(), 2) as round_two, ceil(2.1) as ceil_three, ceiling(2.0) as ceil_two, floor(2.49) as floor_two;
The output below shows the results of executing the Spark SQL query for rounding, ceiling, and floor.
Please see the table below for links to the functions explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | bround | Round to nearest integer using half even algorithm. |
| 2 | round | Round to nearest integer using half up algorithm. |
| 3 | ceiling | Return next largest integer. |
| 4 | floor | Return next smallest integer. |
In a recent article on PostgreSQL, I had to use the floor function because the casting from a decimal to an integer was rounding the number. These functions will come in handy in your future adventures with Spark SQL.
Give Me the Power!
The memory in computers is based upon powers of two. The Spark SQL language supplies the developer with three unique power functions. Remember, fractional powers such as ½ are the same as the square root. The snippet below investigates these functions.
%sql -- -- 7 – whole vs fractional powers -- select cbrt(27) as cube_root_1, sqrt(16) as square_root_1, pow(27, 1/3) as cube_root_2, power(16, 1/2) as square_root_2, power(3, 3) as cubed_three;
The output below is from the above query.
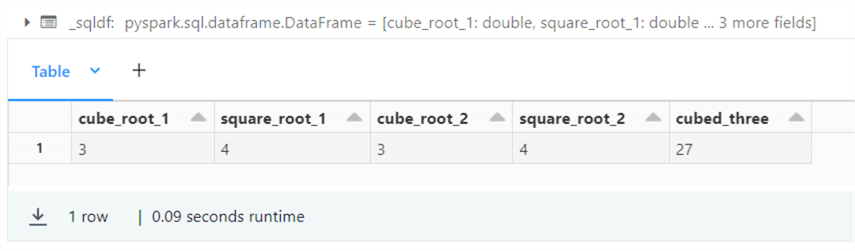
Please see the table below with links to the functions explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | sqrt | Square root of a number. |
| 2 | cbrt | Cube root of a number. |
| 3 | pow | Number x raised to power y. |
| 4 | power | Number x raised to power y. |
In mathematics, exponentiation is one way to express a number x raised to the y power.
Exponential and Factorial Numbers
Leonhard Euler established the fundamental relationship between trigonometric functions and the complex exponential function. The equation uses the base of the natural logarithm [e], imaginary numbers [i], and trigonometry functions of sine [sin] and cosine [cos]. An imaginary number is the square root of negative one. Exponential functions raise e to the power of n. Last, the factorial of n is the product of all positive integers less than or equal to n.
%sql -- -- 8 – Eulers number, exponential, and factorial -- select e() as eulers_number, power(e(), 0) as power_zero, exp(0) as equals_one, expm1(0) as equals_zero, factorial(5) as equals_120;
The above query explores these mathematical numbers. The screenshot below shows the output of the above query.
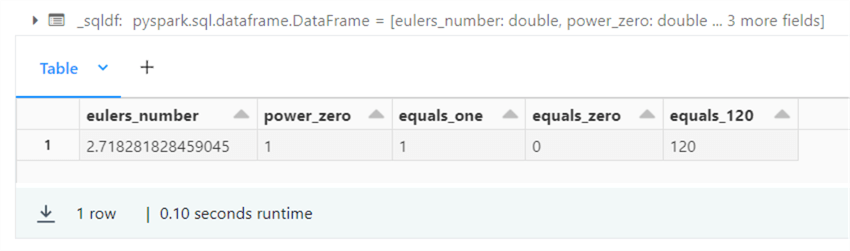
Please see the table below that has links to the functions that were explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | e | Returns Euler's number. |
| 2 | exp | Returns e raised to power n. |
| 3 | exp1m | Returns exp(n) minus 1. |
| 4 | factorial | Returns the factorial n. |
The exponential function arises whenever a quantity grows or decays at a rate proportional to its current value. One such situation is continuously compounded interest.
Logarithmic Functions
The logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. In high school, we used to graph numbers that varied wildly in experiments using a logarithmic scale of base 10.
The Spark SQL query below explores the four functions available to a developer.
%sql -- -- 9 – logarithmic functions -- %sql select log2(128) as base_two, log(3, 27) as base_three, log10(100) as base_ten, log1p(0) as equals_zero;
The screenshot below shows the output of the function calls.
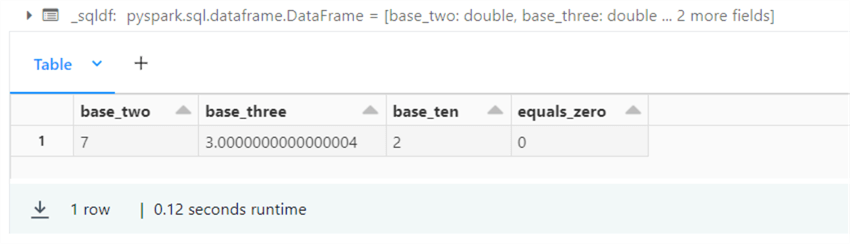
Please see the table below that has links to the functions that were explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | log | Returns logarithm of x base y. |
| 2 | log2 | Returns logarithm of x base 2. |
| 3 | log10 | Returns logarithm of x base 10. |
| 4 | log1p | Return logarithm of 1 + expr. |
| 5 | ln | Returns natural logarithm base e. |
The logarithm scale is handy in displaying wildly varying data in a very compact form.
Greatest vs. Least
The following two functions work on arrays. Given a set of numbers, what is the greatest (largest) value in the set? The opposite of greatest is least. Given a set of numbers, what is the least (smallest) value in the set?
%sql -- -- 10 – greatest vs least in numeric arrays -- %sql select greatest(2, 6, 4) as largest_no, least(1, 3, 5) as smallest_no;
The output from executing the above Spark SQL statement is seen below.
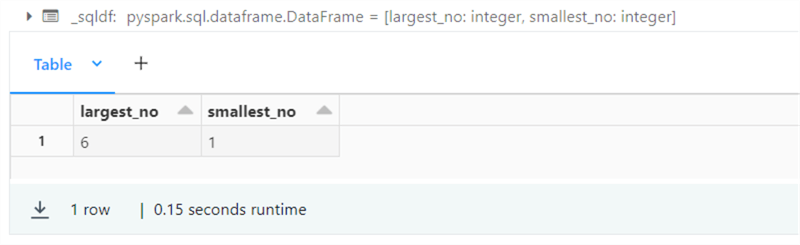
Please see the table below that has links to the functions that were explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | greatest | Return largest number in array. |
| 2 | least | Return smallest number in array. |
I have not had the chance to use these functions with my clients since the max and min aggregate functions are available for numeric columns. But if you have arrays associated with each row, there might be a use case for trying these functions.
Random Numbers
The problem with random number generators is the fact that the same function and the same seed create the same series. The Spark SQL language contains three different functions. Please see the documentation links below. Interestingly, the rand and random functions produce the same series given the same seed.
%sql -- -- 11 – Not so random numbers! -- select rand(0) as func1, random(1) as func2, randn(0) as func3;
The above query creates three random numbers, as seen in the image below.
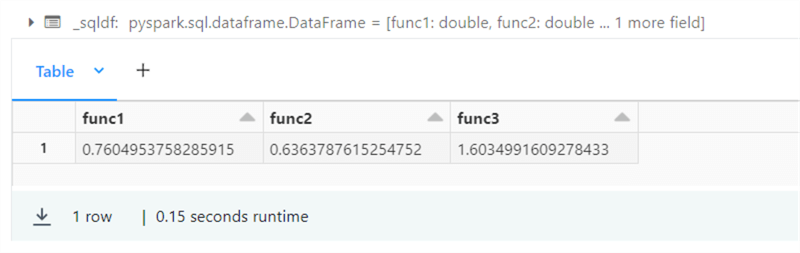
Please see the table below that has links to the functions that were explored in this simple query.
| Example | Function | Description |
|---|---|---|
| 1 | rand | Returns a value between 0 and 1. |
| 2 | randn | Returns a value from a normal distribution. |
| 3 | random | Returns a value between 0 and 1. |
Random number functions are very useful when you are trying to generate test data.
Casting Functions
The format of data is never consistent between systems. Therefore, if you combine payroll data from SAP and JD Edwards in your data lake, you might have to cast data from one type to another. The Spark SQL language supplies the developer with many functions. The sample code below explores these functions.
To save space, any column prefixed with "t_" represents the final type, and any column prefixed with "m_" depicts the maximum value for the given data type. I want you to be aware of potential overflows that can cause a positive number to turn negative.
%sql
--
-- 12 – explore type casting
--
select
bigint(1.9) as t_bigint,
int(0.9) as t_int,
rint(12.56) as t_double,
power(2, 15)-1 as m_smallint,
smallint(pow(2, 15)) as t_smallint,
power(2,7)-1 as m_tinyint,
tinyint(power(2,7)) as t_tinyint,
boolean(0) as t_false,
boolean(1) as t_true,
to_binary('😃', 'utf-8') as t_binary,
to_number('1,454', '9,999') as s2n,
format_number(123456.123456, 4) as n2s;
The output from executing the above Spark SQL statement is seen below. The type-case of large numbers to small and tiny integers results in negative numbers when the maximum value that can be stored is exceeded. The last two functions convert a number to a string and vice versa.
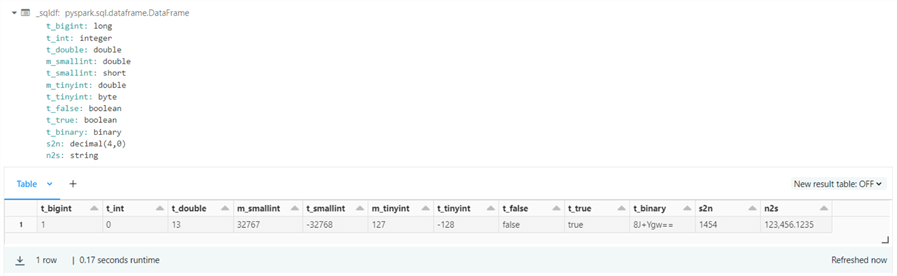
Please see the table below for links to the functions that can be used to cast numeric values from one type to another.
| Example | Function | Description |
|---|---|---|
| 1 | bigint | Convert expression to big integer type. |
| 2 | int | Convert expression to integer type. |
| 3 | rint | Convert expression to double type. |
| 4 | smallint | Convert expression to small integer type. |
| 5 | tinyint | Convert expression to tiny integer type. |
| 6 | boolean | Convert expression to boolean type. |
| 7 | to_binary | Convert expression to binary type. |
| 8 | to_number | Convert a string to a number. |
| 9 | format_number | Convert a number to a string using a format. |
| 10 | decimal | Convert to a decimal type. |
| 11 | double | Convert to a double type. |
In short, we can easily convert from one number format to another using these functions.
Trigonometry Functions
The review of different numeric functions is almost complete. To effectively build structures, humans had to learn about triangles and angles. In geometry, the sum of all the angles in a triangle must equal 180 degrees. However, most mathematicians use radians when solving complex problems. The snippet below shows some relations between pi, degrees, and radians.
%sql -- -- 13 – degrees vs radians -- select degrees(pi()) as half_circle, radians(180) as life_of_pi, 360 / (2 * pi()) as radian_to_degrees;
The image below shows the output of running the above query. We can see that the equation "2 * pi = 360 degrees" is true, and one radian is almost 57.3 degrees.
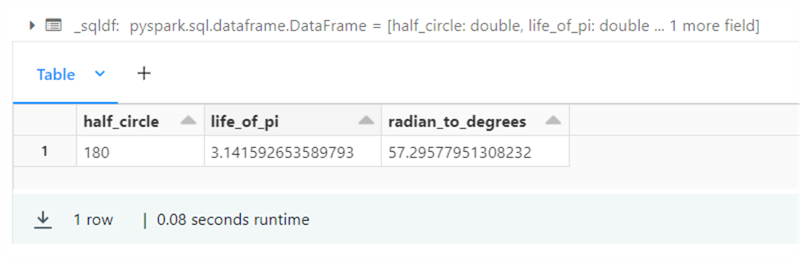
The following two screenshots were taken from a math tutoring for schools website called Third Space Learning. In the capstone section, we will have six problems to solve with right-angled triangles. The ratios of sine, cosine, and tangent of the angle have a relationship to the adjacent, opposite, and hypotenuse sides of the triangle. Please see the image below. We can use these formulas to find the length of a side given one angle and one side.

The inverse trigonometry functions are used when the sides are known and the angle is missing. They are sometimes called arc sine, arc cosine, and arc tangent.

There are a ton of trigonometry functions. I am going to skip the hyperbolic functions. Today, we are going to focus on the following functions.
| Example | Function | Description |
|---|---|---|
| 1 | degrees | Convert radians to degrees. |
| 2 | radians | Convert degrees to radians. |
| 3 | pi | Ratio of circumference to diameter. |
| 4 | sin | Return sine of expression. |
| 5 | cos | Return cosine of expression. |
| 6 | tan | Return tangent of expression. |
| 7 | asin | Return inverse sine of expression. |
| 8 | acos | Return inverse cosine of expression. |
| 9 | atan | Return inverse tangent of expression. |
In the next section, we will use the above formulas to solve six capstone problems.
Capstone Project
Again, I want to thank the Third Space Learning website for these examples. I solved each problem using a Spark SQL formula executed in Azure Databricks. We will review and solve three trigonometry problems and three inverse trigonometry problems.
Trigonometry Problems
Example 1. The triangle has an angle of 30 degrees and an opposite side (0) length of 4 cm. What is the length of the hypotenuse (H)?
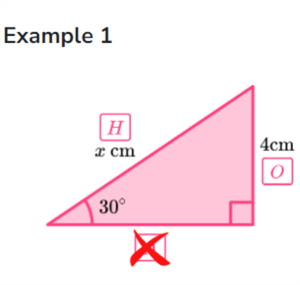
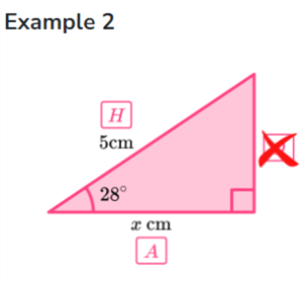
Example 2. The triangle has an angle of 28 degrees and a hypotenuse (H) length of 5 cm. What is the length of the adjacent (A) side?
Example 3. The triangle has an angle of 63 degrees and an adjacent side (A) length of 7 cm. What is the length of the opposite (O) side?
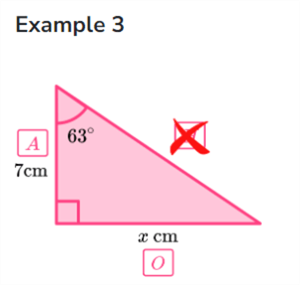
The simple Spark Query below solves our trigonometry problems. The hardest part to remember is that the functions use radians as a measurement type.
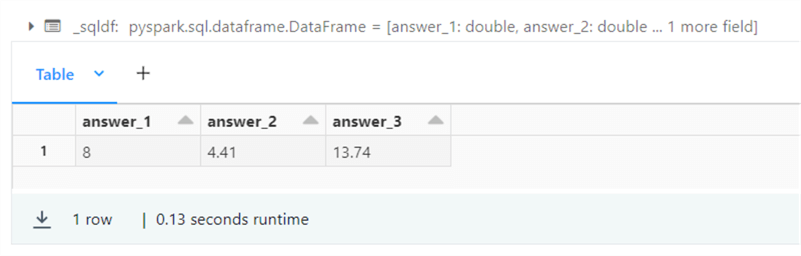
-- -- 14 – Capstone – trigonometric functions -- %sql select round(4 / sin(radians(30)), 2) as answer_1, round(5 * cos(radians(28)), 2) as answer_2, round(7 * tan(radians(63)), 2) as answer_3;
The output below shows the corresponding answers to our three trigonometry problems.
Inverse Trigonometry Problems
Sometimes, we know the length of two sides of the triangle and want to figure out the angle. That is where inverse trigonometry functions come into play.
Example 1. The first example shows a triangle with a hypotenuse side (H) of 10 cm and an opposite side (O) of 5 cm. What is the size of the angle in degrees?
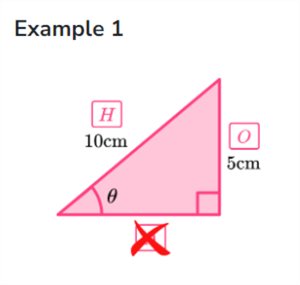
Example 2. The second example shows a triangle with an adjacent side (A) of 4 cm and a hypotenuse side (H) of 5 cm. What is the size of the angle in degrees?
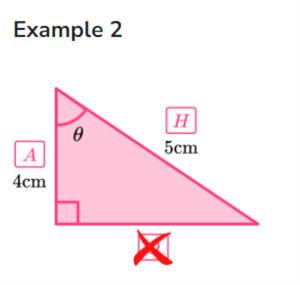
Example 3. The third example shows a triangle with an adjacent side (A) of 8 cm and an opposite side (O) of 12 cm. What is the size of the angle in degrees?
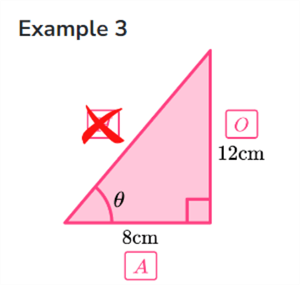
The simple Spark Query below solves our inverse trigonometry problems. The hardest part to remember is that the functions use radians as a measurement type. One must convert to degrees to obtain the correct answer.
-- -- 15 – Capstone – inverse trigonometric functions -- select round(degrees(asin(5/10)), 2) as answer_1, round(degrees(acos(4/5)), 2) as answer_2, round(degrees(atan(12/8)), 2) as answer_3;
The output below shows the corresponding answers to our three inverse trigonometry problems.
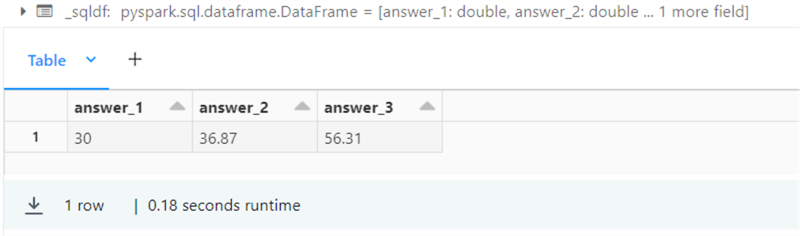
I always loved solving trigonometry problems in high school.
Summary
The Spark language contains a lot of math-related functions. First, we started with basic arithmetic and comparison functions. These functions will be used daily in queries against your datasets that contain numbers. Next, we covered many mathematical functions for rounding, signs, power series, exponential formulas, logarithmic scales, and factorial sequences. While you might not use these functions daily, it is important to know they exist.
Casting numeric data from one type to another is an important technique. Please be cognizant of overflows. Also, the random number function is useful when generating test data. These numbers can be used to perform a lookup in existing tables. For instance, if we want to generate full names from a list of 100 first and 100 last names. Two random numbers can be used to create a new name from two lookups: first name and last name.
Civilization would not have progressed without the understanding of angles and sides. That is how the Ancient Egyptians used rope to understand Pythagoras theorem. Today, we explored how to solve right-angle problems using both trigonometric and inverse trigonometric functions.
To recap, having a good understanding of how to manipulate the basic data types (date/time, numbers, and strings) is very important for the big data engineer. This article focused on basic numeric functions. Enclosed is the notebook used in this article. Next time, we will concentrate on working with string functions.
Next Steps
- Learn about string functions.
- Learn about statistical functions.
- Learn about binary functions.
About the author
 John Miner is a Data Architect at Insight Digital Innovation helping corporations solve their business needs with various data platform solutions.
John Miner is a Data Architect at Insight Digital Innovation helping corporations solve their business needs with various data platform solutions.This author pledges the content of this article is based on professional experience and not AI generated.
View all my tips
Article Last Updated: 2024-03-19






