Multiple Regression Model Enhanced with Bagging

By: Rick Dobson   |   Updated: 2021-01-08   |   Comments   |   Related: > TSQL

Problem

I read that bagging is one of several data science ensemble methods that can result in better model fits to a dataset.  Please clarify what bagging is relative to a basic decision tree model.  Also, demonstrate how to apply bagging for better multiple regression model fits to data from SQL Server.

Solution

Ensemble methods are a broad class of data science modeling techniques that aim to improve how a model fits some data.  Bagging, more formally called bootstrap aggregation, is a particularly easy ensemble method.  The popularity of bagging may come from its core feature of creating smaller "bags" of dataset rows from a larger dataset with many rows.  Each bag is composed of a random sample with replacement from the larger dataset.  The models for each bag of data are then aggregated into an overall bagged model.  A prime benefit of bagging is that it can reduce model variance relative to a single model estimated from the original larger dataset.  That is, the aggregated model estimated on multiple bags will fit the underlying data more closely (with less model variance) than a model based on the original larger dataset from which the samples are drawn.

Bagging works especially well for improving the fit of decision tree classification and regression models.  This tip is a case study of how to build a bagged model for estimating snowfall observations made at weather stations.  The model specifies that the amount of snowfall depends on the locale and season during which an observation is made.  The locale for an observation can be specified by the longitude and latitude of the weather station from which the observation was made.  A prior tip, T-SQL Code for the Decision Tree Algorithm – Part 3, illustrates how to build a decision tree regression model for this data.  After you initially explore a dataset and build a model for the dataset rows, you are likely to be able to build an improved model with bagging.  Data scientists often specify a bagging model's overall design from a single initial model based on all the dataset rows.

A main objective of this tip series is to grow an understanding among T-SQL developers of classic data science models.  To facilitate this goal, models are built with T-SQL code.

Data for this tip

The dataset for this tip consists of 294 rows of snowfall weather observations.  Each observation is from a weather station with a locale specified by latitude and longitude coordinates as well as the quarter within a year for the years from 2016 through 2019.  The weather stations reside in one of three states: New York (NY), Illinois (IL), or Texas (TX).  The data are derived from a SQL Server weather data warehouse.

Data science projects can require a fair amount of initial processing to configure source data for input to a model; this project is no exception to the general rule.  Nearly all the data wrangling code is described in a prior tip T-SQL Code for the Decision Tree Algorithm – Part 3.  Therefore, this section just reacquaints you with the basic dataset layout and one new line of code that is critical for the bagging application demonstrated in this tip.  The full set of data wrangling code is also available in the download for this tip.

The following screenshot shows the first ten weather observation rows from the original source dataset for this tip.  The data in the screen shot are from the rows of the #for_sd_reduction_with_date_and_geog_bins temp table.

• As you can see from the STATEPROV column values, all these rows are from a weather station in TX.
• The noaa_station_id column contains an identifier code (013962) for the weather station where the observations were recorded.  There are a handful of weather stations contributing weather observations from each of the three states in the data science project.
• The snowy_quarter_indicator column has a "wintery quarter" code value for observations made during either Q1 or Q4.  Observations made during either Q2 or Q3 are assigned a "non_wintery quarter" code value.
• The long_dec_degree_one_third_tile_indicator column classifies stations from TX with a west_east_west_indicator value.  All weather stations in Texas are in the most western third of longitude values in this dataset.
• The snow_avg column displays the average snowfall in inches for the observations during a quarter.
• The lat_dec_degree_one_third_tile_indicator column classifies stations from TX with a north_south_south_indicator value.  All weather stations in Texas are in the most southern third of latitude values in the dataset.
• A prior analysis of these data confirmed that
  • The long_dec_degree_one_third_tile_indicator values correlated better with snowfall at a station than lat_dec_degree_one_third_tile_indicator values.
  • Lat_dec_degree_one_third_tile_indicator values added no significant incremental explanatory capability when long_dec_degree_one_third_tile_indicator values were already in the model.

The row_id column in the following screenshot is a new column that was not in the prior tip that analyzed this dataset.  The row_id column is populated by the following select list item in the script for populating the #for_sd_reduction_with_date_and_geog_bins table.  The order by clause within the function specifies the order for rows in the results set.  The assignment of a distinct row_id column value for each row within the #for_sd_reduction_with_date_and_geog_bins table facilitates the specification of randomized rows in separate bags of rows.

row_number() over (order by noaa_station_id, year, quarter) row_id

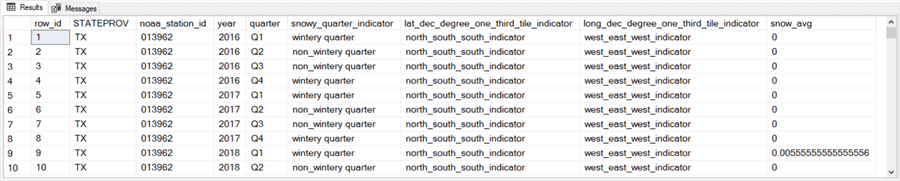
The next screenshot shows the first ten rows for a weather station in NY.  The weather station has an identification value of 014735.  As you can see, the results set showing observations from a NY weather station has the same layout as the results set showing rows from a weather station in TX.

• All the rows in the screenshot as well as the rest of the rows for weather stations from NY have a long_dec_degree_one_third_tile_indicator column value of west_east_east_indicator value.
• Additionally, only two rows in the following screenshot have a zero value for the snow_avg column.  In contrast, the preceding screenshot showing weather observations from a TX weather station has nine rows with a zero value in the snow_avg column.

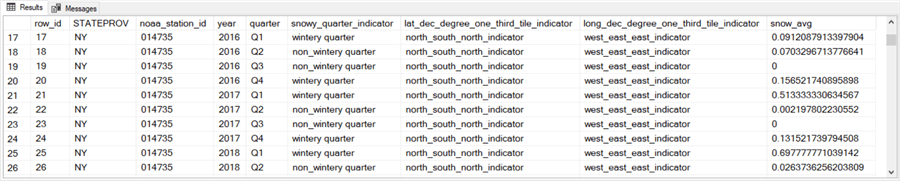
The next screen shot shows the first ten rows for a weather station in IL.

• All ten of the rows have a long_dec_degree_one_third_tile_indicator column value of west_east_middle_indicator.  This long_dec_degree_one_third_tile_indicator column value assignment is typical of all other observations from IL.

• Additionally, notice that the number of snow_avg column values that are zero is four.  This value is in between the number of zero values for the snow_avg column from the first ten weather rows from TX and the first ten weather rows from NY.

To facilitate the fitting of the bagged model to the data, a backup copy of the rows in the #for_sd_reduction_with_date_and_geog_bins table is made.  The name of the table with the backup data is #backup_of_#for_sd_reduction_with_date_and_geog_bins.

How to create and unit test bag samples

This section of the tip demonstrates how to designate five sets of eighty row_id values each.  Each set of row_id values corresponds to a bag of row_id values from the #for_sd_reduction_with_date_and_geog_bins table.  Therefore, the row_id values within each set can have values from 1 through 294.  The row_id values within each bag are drawn from a uniform random distribution based on the T-SQL rand function.  Because successive values are selected independently, it is possible for the same randomly selected row_id to reside more than once within each bag of row_id values.

The following script shows the T-SQL code for populating the #rand_digits temporary temp table with the five sets of eighty row_id values each.  There are three main steps in the script.

• The first step creates a fresh version of the #rand_digits temp table. 
• The second step declares and assigns values to local variables for controlling passes through a pair of nested while loops.
  • The outer loop is for each of the five bags.
  • The inner loop is for the eighty rows within each bag.
• The third step populates the #rand_digits temporary table by passing through the nested while loops 400 times for a total of eighty rows in each of five bags.

As you can see, the temp table has three columns.

• The sample_id column is a tinyint field to designate the sample.  This column will hold values of 1 through 5 for the first through the fifth bag.
• Row_id is the row order within a bag.  The range of values for this column is 1 through 80.
• Rand_digit is a pseudo random number based on the T-SQL rand function embedded in an expression.  Each rand_digit value generated by the following script can be in the range of 1 through 294.  These rand_digit values point at row_id values within the #for_sd_reduction_with_date_and_geog_bins table.

-- This code sample returns five sets of a uniform random distribution of 
-- digits in the range from @min_integer (1) through @max_integer (294)
 
 -- step 1: create a fresh copy of #rand_digits
begin try
drop table #rand_digits
end try
begin catch
   print '#rand_digits not available to drop'
end catch
 
create table #rand_digits
(
 sample_id tinyint
,row_id int
,rand_digit int
)
 
-- step 2: declare min and max random digit values
-- and variables values to control loop count
declare 
 @sample_ctr tinyint = 1
,@max_sample tinyint = 5  -- number of samples
,@loop_ctr int
,@max_loop_ctr int = 80  -- number of random row_id values per sample
,@min_integer tinyint =   1
,@max_integer int =  294  -- number of row_id values in original source data  
 
-- step 3: loop @max_max_sample times across samples
while @sample_ctr <= @max_sample
begin
   set @loop_ctr = 0
 
-- loop @max_loop_ctr times in a sample
   while @loop_ctr < @max_loop_ctr
   begin
 
   -- generate a random digit sequence with 
   -- values from @min_integer through @max_integer
   -- and insert it into #rand_digits 
   insert #rand_digits
   select 
      @sample_ctr
     ,@loop_ctr+1 row_id
     ,floor(rand()*(@max_integer - @min_integer + 1) + @min_integer) rand_digit
 
   set @loop_ctr = @loop_ctr + 1
 
   end
 
set @sample_ctr = @sample_ctr + 1
 
end

Here are a few sample scripts to unit test the results from the preceding script.

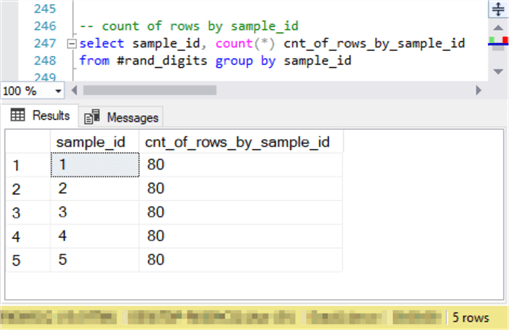
The following script counts the number of rows by sample_id value in #rand_digits.  Notice there are precisely 80 rows per sample_id value.  The sample_id values extend from 1 through 5.

The next screenshot shows a script segment to return the number of rand_digit values within each sample as denoted by sample_id.

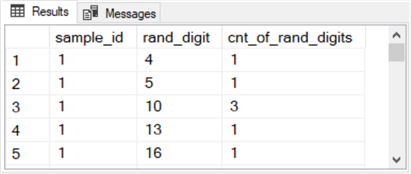
Here are the first five rows of output for sample_id 1.  Notice there are three instances of a rand_digit with a value of 10.

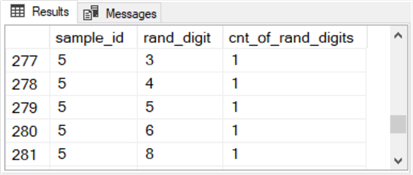
Here are the first five rows of output for sample_id 5.  In this set of rows, there are no duplicate values in the first five rows of the fifth bag.  Recall that duplicate values are legitimate because successive rand_digit values within a bag are independently drawn from a uniform random distribution with replacement.

When you use a pseudo random number generator, such as the rand function, you will not obtain identical results on successive re-runs of your application.  This is because the rand function strives to return values which are from a uniform random distribution.  This will not be a problem in normal use case applications.  However, if you need to preserve the results for unit testing or some other kind of requirement, you can save a set of pseudo random numbers and restore the exact same random numbers for successive re-runs of an application.  The download for this tip contains two additional scripts that support a store and re-use requirement.

• The first script saves the values in the #rand_digits temporary table in the dbo.backup_for_last_#rand_digits table within the default database.  By saving the rows from the #rand_digits temporary table in the dbo.backup_for_last_#rand_digits table, we enable the capability to re-run the data science solution with the same set of random digits.  This capability was particularly valuable when unit testing the code for this tip.
• The second script saves the row_id values from the #for_sd_reduction_with_date_and_geog_bins temp table that are not referenced in the #rand_digits table.  The saved values are retained in the dbo.hold_out_sample_for_bagging table of the default database.  A follow-up tip will use the hold-out sample to help assess the accuracy of the model for a sample of weather observations that was not used to train the bagged model.

Presenting models without bagging and with bagging

The following screen shot shows the Decision Tree Model from a prior tip T-SQL Code for the Decision Tree Algorithm – Part 3 for the data analyzed with the bagging ensemble method in this tip. The results are very briefly reviewed because they are discussed at length in the prior tip and the results from the prior tip are meant to serve as comparative purposes.

• The model starts with the root node based on 294 rows of data. The average daily snow across all rows is .0965 inches.
• The root node separates into three additional nodes at the first level. The separation is based on the longitudinal value for each weather station from which observations were made.  The three node names are
  • we_east_indicator rows which is for the third of longitudinal values that are east most.  The 97 observations in this node have the most amount of snowfall.
  • we_middle_indicator rows which is for the middle set of longitudinal values between the east most and west most values. The 89 observations in this node has less snowfall on average than the we_east_indicator rows and more snowfall than we_west_indicator rows.
  • we_west_indicator rows which is for the third of longitudinal values that are west most.  The 108 observations in this node have the least amount of snowfall.
• The six leaf nodes are all child nodes to the three first-level nodes.

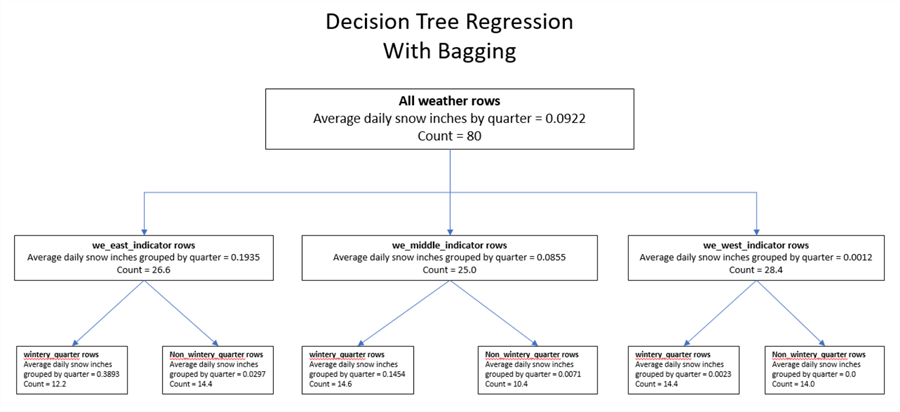
The next screenshot shows an adaption of the preceding decision tree regression model diagram based on the bagging ensemble method implemented in this tip.  While a decision tree diagram is used to display the results, the model is really an aggregated model based on five separate bags.  Whereas the preceding diagram is for a single model based on 294 individual observations, the following diagram is for the average of 400 dataset rows – some of which are repeats of other rows because of sampling with replacement for populating bags.

• The root node shows an average count of just 80.  This is because each bag is comprised of 80 weather rows.  Therefore, the average sample size is 80 across the five bags.  Also, the snowfall on average for the root node observations is slightly less than for the decision tree diagram in the preceding screen shot.
• The three nodes below the root node show the average snowfall and count for the three longitudinal segments.  The sum of the average counts for these three nodes (26.6, 25.0, and 28.4) is 80, which is the average count for the root node.
• The bottom set of six nodes are for wintery_quarter rows and non_wintery quarter rows.  Each first-level node divides into two nodes – one for wintery_quarter rows and a second for non_wintery quarter rows.
  • The sum of the average counts for each pair of leaf child nodes equals the average counts for the parent node of each pair.
  • Also, the average snowfall for each member of a pair of leaf nodes bound the average snowfall for each parent node.  That is, the snowfall for each first-level node falls between its two child nodes (for wintery_quarter rows and non_wintery quarter rows).
  • Again, the average snowfall for the leaf nodes in the bagged model fit is slightly different than for the decision tree regression model based on all individual rows in the source data set.
• The main purpose of the next section is to convey the highlights of how to compute values for populating the following diagram.
• A follow-up tip will compare the decision tree regression model with the bagged regression model.

T-SQL code for building a bagged model

The T-SQL code presented in this section illustrates key design features for generating the data for a diagram like the preceding one.  The T-SQL code for building a bagged model in this tip accepts as input source dataset rows (#backup_of_#for_sd_reduction_with_date_and_geog_bins) and a table (#rand_digits) denoting bags of randomly selected source data row_id values.  There are three main segments to the T-SQL code.

• The first segment creates key tables as well as declares local variables to prepare for the creation of the bagged model.
• The second segment generates means and counts as well as selected other values for each of the ten nodes in the preceding diagram for each of the five bags used in this tip.
• The third segment averages the means and counts from each bag of dataset rows to create the aggregated values displayed in the preceding diagram.

Here is the code from the first segment.

• The segment starts by conditionally dropping and recreating a fresh version of the #temp_for_bin_rows temp table.  This table is populated at multiple points in the second segment.  Its role is to hold a results set from which to compute snowfall averages and counts for the nine nodes below the root node for a bag.
• Next, the script excerpt conditionally drops and recreates a fresh version of the #results_from_samples temp table.  This table will be used to store a separate row for each of the ten nodes in the preceding diagram for each of the five bags in this data science project.  Each row in the table has columns
  • To identify bag number (sample_no) and node_id value
  • For the mean amount of snowfall (mean) and the sample size (n) for a node
  • Along with two additional values (stdevp for population standard deviation and cv for coefficient of variation) that can assist in interpreting the results within a bag
• This segment concludes with a declare statement for some local variables used to store intermediate values for the ten nodes computed for each bag.  Assignment statements in the second segment reveal the role of each of the local variables declared in the first segment.

-- create and populate #temp_for_bin_rows table
begin try
drop table #temp_for_bin_rows
end try
begin catch
   print 'drop table #temp_for_bin_rows table not available to drop'
end catch
 
-- create a fresh copy of #results_from_samples
begin try
drop table #results_from_samples
end try
begin catch
   print '#results_from_samples not available to drop'
end catch
 
create table #results_from_samples
(
sample_no tinyint
,node_id nvarchar(50)
,mean float
,[stdevp] float
,n float
,cv float
)
go
 
-- declare local variables
 
declare 
@target_mean float, @target_stdevp float, @target_n float, @target_cv float
,@wintery_q_mean float, @wintery_q_stdevp float, @wintery_q_n float, @wintery_q_cv float
,@non_wintery_q_mean float, @non_wintery_q_stdevp float, @non_wintery_q_n float, @non_wintery_q_cv float
 
,@we_east_indicator_mean float, @we_east_indicator_stdevp float, @we_east_indicator_n float, @we_east_indicator_cv float
,@we_middle_indicator_mean float, @we_middle_indicator_stdevp float, @we_middle_indicator_n float, @we_middle_indicator_cv float
,@we_west_indicator_mean float, @we_west_indicator_stdevp float, @we_west_indicator_n float, @we_west_indicator_cv float

Here is the code for the second segment.  This segment makes five passes through a while loop.  Each pass though the loop is for one of the five bags of dataset rows.

• The segment commences by declaring and assigning values to two local variables (@sample_ctr and @max_sample).  These local variable values control the number of passes through the while loop.
• The code within the while loop is bounded by a begin…end statement.  The code within this statement is executed for each of the five bags.
• There are four major steps within the begin…end statement.
  • Step 0 is for the root node.
    • This step starts by extracting the dataset rows for a  bag and storing them in #for_sd_reduction_with_date_and_geog_bins, which changes for each pass through the while loop.  The select statement to extract the sample data rows relies on an inner join of the #backup_of_#for_sd_reduction_with_date_and_geog_bins and #rand_digits temp tables, which both stay the same for all passes through the while loop.
    • Then, step 0 code computes target_mean, target_n, target_stdevp, and target_cv.
      • This tip only utilizes the target_mean and target_n
      • The other two values (target_stdevp and target_cv) can be of use when analyzing the results for an individual bag of dataset rows
    • The step concludes by inserting the computed values into the #results_from_samples table.
  • Step 1 is for the we_east_indicator rows node as well as its two child nodes (wintery_quarter rows node and non_wintery_quarter rows node). 
    • The code computes mean, n, stdevp, and cv values for the rows in each node.
    • After computing the scalar quantities, they are inserted into the #results_from_samples table as three separate rows.
  • Steps 2 and 3 perform analogous operations, respectively, for the we_middle_indicator rows node with its two child nodes and the we_west_indicator rows node with its two child nodes.  As a result, these steps add six more rows to the #results_from_samples table.
  • After step 3 completes, the @sample_ctr local variable is incremented by one.  This local variable keeps track of successive passes through the while loop.

-- declare min and max random digit values
-- and variables values to control loop count
declare 
 @sample_ctr tinyint = 1
,@max_sample tinyint = 5  -- number of samples
 
-- loop @max_max_sample times across samples
while @sample_ctr <= @max_sample
begin
 
-- display sample value
select @sample_ctr [results for sample]
  
   -- pull source data for @sample_ctr
 
   -- truncate #for_sd_reduction_with_date_and_geog_bins table
   truncate table #for_sd_reduction_with_date_and_geog_bins
 
   -- step 0: repopulate #for_sd_reduction_with_date_and_geog_bins table for @sample_ctr
   insert into #for_sd_reduction_with_date_and_geog_bins
   select 
    #rand_digits.rand_digit 
   ,STATEPROV
   ,noaa_station_id
   ,year
   ,quarter
   ,snowy_quarter_indicator
   ,lat_dec_degree_one_third_tile_indicator
   ,long_dec_degree_one_third_tile_indicator
   ,snow_avg
   from #backup_of_#for_sd_reduction_with_date_and_geog_bins
 
   inner join
 
   #rand_digits
   on #rand_digits.rand_digit = #backup_of_#for_sd_reduction_with_date_and_geog_bins.row_id
   where sample_id = @sample_ctr
  
   -- compute and insert into #results_from_samples 
   -- mean, standard deviation, n, and coefficient of determination 
   -- for target col (snow_avg) based on all rows
 
   select 
    @target_mean = avg(snow_avg)
   ,@target_stdevp = stdevp(snow_avg)
   ,@target_n =  count(*)
   ,@target_cv = (@target_stdevp/@target_mean) * 100
   from 
   #for_sd_reduction_with_date_and_geog_bins
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'All weather rows' Node_id
   ,@target_mean [@target_mean]
   ,@target_stdevp [@target_stdevp]
   ,@target_n [@target_n]
   ,@target_cv [@target_cv]
 
 
   -- step 1: compute and assign mean, standard, n, and coefficient of determination 
   -- for west_east_east_indicator rows
 
   if @sample_ctr = 1
      begin
         -- freshly populate #temp_for_bin_rows table with we_east_indicator rows
         select * 
         into #temp_for_bin_rows 
         from #for_sd_reduction_with_date_and_geog_bins 
         where long_dec_degree_one_third_tile_indicator = 'west_east_east_indicator'
      end
   else
      begin
         -- truncate table #temp_for_bin_rows
         -- freshly populate #temp_for_bin_rows table with we_east_indicator rows
         truncate table #temp_for_bin_rows
         insert into #temp_for_bin_rows
         select * 
         from #for_sd_reduction_with_date_and_geog_bins 
         where long_dec_degree_one_third_tile_indicator = 'west_east_east_indicator'
      end
 
   select  
    @we_east_indicator_mean = avg(snow_avg)
   ,@we_east_indicator_stdevp = stdevp(snow_avg)
   ,@we_east_indicator_n =  count(*)
   ,@we_east_indicator_cv = (@we_east_indicator_stdevp/@we_east_indicator_mean) * 100
   from #temp_for_bin_rows
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'we_east_indicator rows' Node_id
   ,@we_east_indicator_mean [@we_east_indicator_mean]
   ,@we_east_indicator_stdevp [@we_east_indicator_stdevp]
   ,@we_east_indicator_n [@we_east_indicator_n]
   ,@we_east_indicator_cv [@we_east_indicator_cv]
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   insert into #temp_for_bin_rows 
   select * 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_east_indicator'
   and snowy_quarter_indicator = 'wintery quarter'
 
   select  
    @wintery_q_mean = avg(snow_avg)
   ,@wintery_q_stdevp = stdevp(snow_avg)
   ,@wintery_q_n =  count(*)
   ,@wintery_q_cv = (@wintery_q_stdevp/@wintery_q_mean) * 100
   from #temp_for_bin_rows
 
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'east_wintery_quarter rows' Node_id
   ,@wintery_q_mean [@wintery_q_mean]
   ,@wintery_q_stdevp [@wintery_q_stdevp]
   ,@wintery_q_n [@wintery_q_n]
   ,@wintery_q_cv [@wintery_q_cv]
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   insert into #temp_for_bin_rows 
   select * 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_east_indicator'
   and snowy_quarter_indicator = 'non_wintery quarter'
 
   select  
    @non_wintery_q_mean = avg(snow_avg)
   ,@non_wintery_q_stdevp = stdevp(snow_avg)
   ,@non_wintery_q_n =  count(*)
   ,@non_wintery_q_cv = (@non_wintery_q_stdevp/@non_wintery_q_mean) * 100
   from #temp_for_bin_rows
 
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'east_non_wintery_quarter rows' Node_id
   ,@non_wintery_q_mean [@non_wintery_q_mean]
   ,@non_wintery_q_stdevp [@non_wintery_q_stdevp]
   ,@non_wintery_q_n [@non_wintery_q_n]
   ,@non_wintery_q_cv [@non_wintery_q_cv]
 
 
   -- step 2: compute and assign mean, standard, n, and coefficient of determination 
   -- for west_east_middle_indicator rows
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   -- freshly populate #temp_for_bin_rows table with we_middle_indicator rows
   insert into #temp_for_bin_rows
   select * 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_middle_indicator'
 
   -- compute for target
   select  
    @we_middle_indicator_mean = avg(snow_avg)
   ,@we_middle_indicator_stdevp = stdevp(snow_avg)
   ,@we_middle_indicator_n =  count(*)
   ,@we_middle_indicator_cv = (@we_middle_indicator_stdevp/@we_middle_indicator_mean) * 100
   from #temp_for_bin_rows
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'we_middle_indicator rows' Node_id
   ,@we_middle_indicator_mean [@we_middle_indicator_mean]
   ,@we_middle_indicator_stdevp [@we_middle_indicator_stdevp]
   ,@we_middle_indicator_n [@we_middle_indicator_n]
   ,@we_middle_indicator_cv [@we_middle_indicator_cv]
 
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   insert into #temp_for_bin_rows 
   select * 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_middle_indicator'
   and snowy_quarter_indicator = 'wintery quarter'
 
   -- compute for wintery rows
   select  
    @wintery_q_mean = avg(snow_avg)
   ,@wintery_q_stdevp = stdevp(snow_avg)
   ,@wintery_q_n =  count(*)
   ,@wintery_q_cv = (@wintery_q_stdevp/@wintery_q_mean) * 100
   from #temp_for_bin_rows
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'middle_wintery_quarter rows' Node_id
   ,@wintery_q_mean [@wintery_q_mean]
   ,@wintery_q_stdevp [@wintery_q_stdevp]
   ,@wintery_q_n [@wintery_q_n]
   ,@wintery_q_cv [@wintery_q_cv]
 
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   insert into #temp_for_bin_rows 
   select * 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_middle_indicator'
   and snowy_quarter_indicator = 'non_wintery quarter'
 
   -- compute for non_wintery rows
   select  
    @non_wintery_q_mean = avg(snow_avg)
   ,@non_wintery_q_stdevp = stdevp(snow_avg)
   ,@non_wintery_q_n =  count(*)
   ,@non_wintery_q_cv =
   case
      when @non_wintery_q_mean = 0 then null
      else (@non_wintery_q_stdevp/@non_wintery_q_mean) * 100
    end
   from #temp_for_bin_rows
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'middle_non_wintery_quarter rows' Node_id
   ,@non_wintery_q_mean [@non_wintery_q_mean]
   ,@non_wintery_q_stdevp [@non_wintery_q_stdevp]
   ,@non_wintery_q_n [@non_wintery_q_n]
   ,@non_wintery_q_cv [@non_wintery_q_cv]
 
 
   -- step 3: compute and assign mean, standard, n, and coefficient of determination 
   -- for west_east_west_indicator rows
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   -- freshly populate #temp_for_bin_rows table with we_west_indicator rows
   insert into #temp_for_bin_rows
   select * 
   --into #temp_for_bin_rows 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_west_indicator'
 
   -- compute for west_east_west_indicator rows
   select  
    @we_west_indicator_mean = avg(snow_avg)
   ,@we_west_indicator_stdevp = stdevp(snow_avg)
   ,@we_west_indicator_n =  count(*)
   ,@we_west_indicator_cv =
   case
      when @non_wintery_q_mean = 0 then null
      else (@non_wintery_q_stdevp/@non_wintery_q_mean) * 100
    end
   from #temp_for_bin_rows
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'we_west_indicator rows' Node_id
   ,@we_west_indicator_mean [@we_west_indicator_mean]
   ,@we_west_indicator_stdevp [@we_west_indicator_stdevp]
   ,@we_west_indicator_n [@we_west_indicator_n]
   ,@we_west_indicator_cv [@we_west_indicator_cv]
 
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   insert into #temp_for_bin_rows 
   select * 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_west_indicator'
   and snowy_quarter_indicator = 'wintery quarter'
 
   -- compute for wintery results rows
   select  
    @wintery_q_mean = avg(snow_avg)
   ,@wintery_q_stdevp = stdevp(snow_avg)
   ,@wintery_q_n =  count(*)
   ,@wintery_q_cv =
   case
      when @non_wintery_q_mean = 0 then null
      else (@non_wintery_q_stdevp/@non_wintery_q_mean) * 100
    end
   from #temp_for_bin_rows
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'west_wintery_quarter rows' Node_id
   ,@wintery_q_mean [@wintery_q_mean]
   ,@wintery_q_stdevp [@wintery_q_stdevp]
   ,@wintery_q_n [@wintery_q_n]
   ,@wintery_q_cv [@wintery_q_cv]
 
 
   -- clear #temp_for_bin_rows table
    truncate table #temp_for_bin_rows 
 
   insert into #temp_for_bin_rows 
   select * 
   from #for_sd_reduction_with_date_and_geog_bins 
   where long_dec_degree_one_third_tile_indicator = 'west_east_west_indicator'
   and snowy_quarter_indicator = 'non_wintery quarter'
 
 
   -- compute for non_wintery results rows
   select  
    @non_wintery_q_mean = avg(snow_avg)
   ,@non_wintery_q_stdevp = stdevp(snow_avg)
   ,@non_wintery_q_n =  count(*)
   ,@non_wintery_q_cv = 
    case
      when @non_wintery_q_mean = 0 then null
      else (@non_wintery_q_stdevp/@non_wintery_q_mean) * 100
    end
   from #temp_for_bin_rows
 
   -- add a row to #results_from_samples
   insert into #results_from_samples
   select
    @sample_ctr [sample_no]
   ,'west_non_wintery_quarter rows' Node_id
   ,@non_wintery_q_mean [@non_wintery_q_mean]
   ,@non_wintery_q_stdevp [@non_wintery_q_stdevp]
   ,@non_wintery_q_n [@non_wintery_q_n]
   ,@non_wintery_q_cv [@non_wintery_q_cv]
 
   select * from #results_from_samples
 
set @sample_ctr = @sample_ctr + 1
 
end			

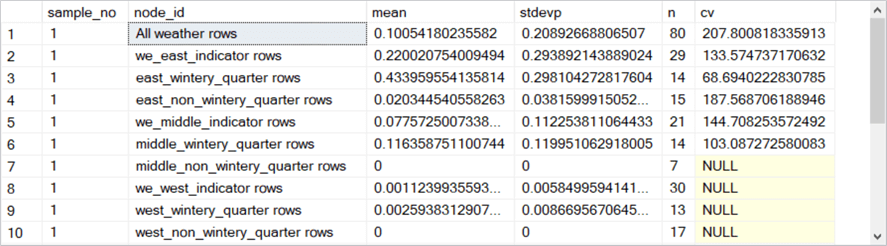
Here is a collection of five screen shots that shows the rows in the #results_from_samples table populated by the preceding script.

• The sample_no column within each screen shot denotes the bag number.  There are five bags numbered 1 through 5.
• The node_id value contains a string value that indicates the type of rows summarized on a row for a bag.
  • For example, the first row in the first screen shot has a node_id value of all weather rows – namely, rows for the root node.  This row is for all 80 rows in the first bag.
  • The rows with node_id value of we_east_indicator rows, we_middle_indicator rows, and we_west_indicator rows point at the three nodes immediately below the root node.  The n column values for the three rows (29, 21, and 30) sum to 80, which is the n column value for their parent node.
  • The six remaining rows with a sample_no value of 1 denote leaf nodes in the model for the first bag.
  • The rows for sample_no values of 2 through 5 point to corresponding nodes for the second through the fifth bags.

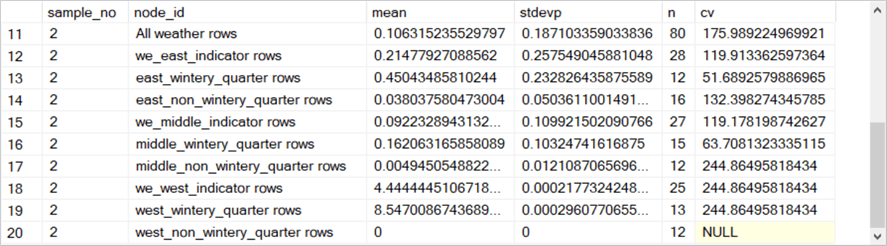
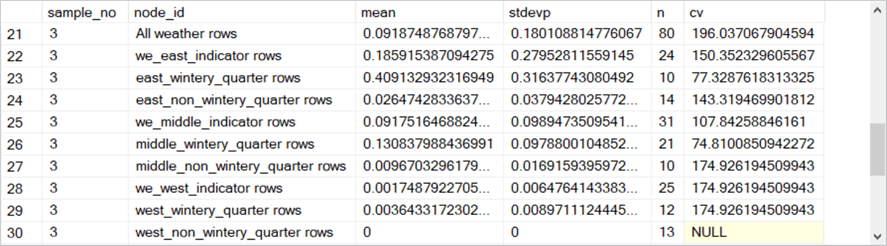
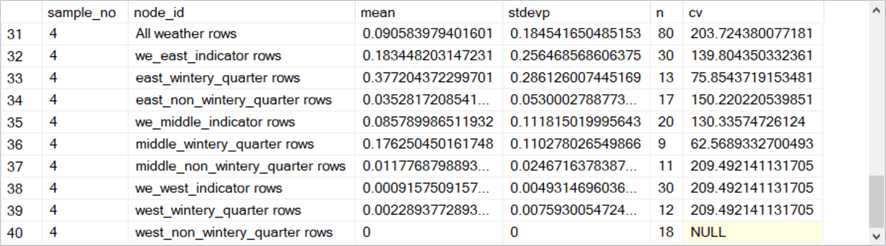
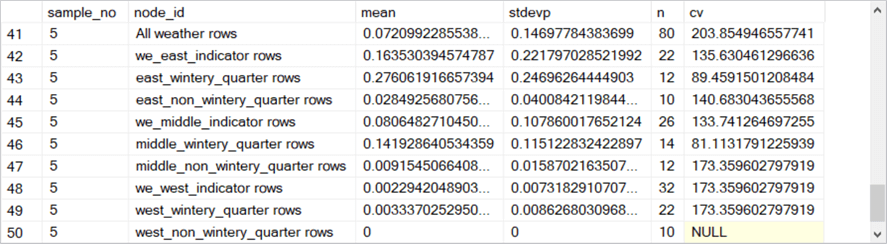
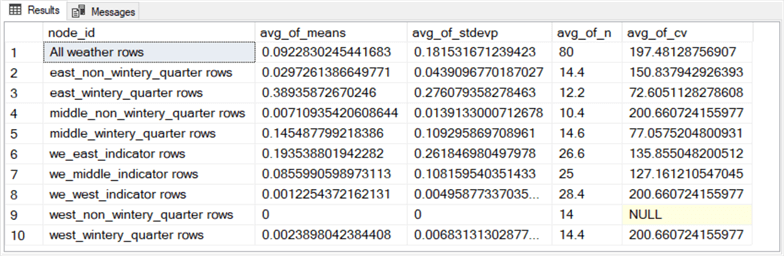
The fifty rows in the preceding collection of screenshots needs to be averaged by node_id value to compute the average snowfall (avg_of_means) and average count of rows (avg_of_n) for the bagged multiple regression model.  The following T-SQL script shows how easy it is to compute the average snowfall and count of observations for each node of the bagged regression model.  As you can see, the script also computes average values for population standard deviation (avg_of_stdevp) and coefficient of variation (avg_of_cv).  These latter two averages are sometimes used to assist in interpreting the model fit results.

-- compute average values for mean snowfall, stdevp for snowfall, 
-- number of observations for snowfall (n), and coefficient of variation
-- group by decision tree node
select 
node_id
,avg(mean) avg_of_means
,avg(stdevp) avg_of_stdevp
,avg(n) avg_of_n
,avg(cv) avg_of_cv
from #results_from_samples
group by node_id

The following screenshot displays the results set from the preceding script.

• Each row of values represents an average across the five bags in the data science project for this tip.
• The second decision tree diagram within the "Presenting models without bagging and with bagging" section of this tip displays the avg_of_means (for average daily snow by quarter) and avg_of_n (for Count) for the bagged model.
• While it is possible and even instructive to display the results set below in a decision tree, the output is not strictly speaking a decision tree model.  This is because the bagged model is really an average of five decision tree models – namely, one for each bag in this tip.

Next Steps

This tip's download includes a .sql file for performing the case study demonstrated in this tip, an Excel workbook file with sample datasets showing the data inputs for the .sql file, and a PowerPoint file with two decision tree diagrams for displaying the aggregated bagged model and a previous decision tree regression model estimated with the standard deviation reduction method.  There are four parts to the case study.  A fifth bullet in the following list is for creating a decision tree diagram for displaying the bagged model.

• Draw the initial sample or 294 rows from a data warehouse (or collect the rows from the Excel file with the original dataset rows).
• Draw five random samples with replacement of 80 rows each from the original dataset of 294 rows created in the preceding step.
• Estimate a model for each of the five sets or random row_id values.
• Average the model fits across the five random samples of 80 rows each.
• Display and compare via a PowerPoint presentation file decision tree diagrams for an original decision tree regression model versus the average bagged model.

After you confirm the sample works for the code and data in the download for this tip, you can implement the same general approach with some confidence to data from your organization.

The bagging model estimation technique is the object of many web pages around the internet.

• Here is a basic presentation of bagging: Bagging
• A more advanced presentation of bagging is available from this seminal source: Bagging Predictors
• You will often discover bagging presented along with complementary data science techniques; see, for example, these references: Ensemble methods: bagging, boosting and stacking and Bagging Vs Boosting In Machine Learning

About the author

Rick Dobson is an author and an individual trader. He is also a SQL Server professional with decades of T-SQL experience that includes authoring books, running a national seminar practice, working for businesses on finance and healthcare development projects, and serving as a regular contributor to MSSQLTips.com. He has been growing his Python skills for more than the past half decade -- especially for data visualization and ETL tasks with JSON and CSV files. His most recent professional passions include financial time series data and analyses, AI models, and statistics. He believes the proper application of these skills can help traders and investors to make more profitable decisions.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips