Build a Web Crawler in Python for a Website Content Audit

By: Nai Biao Zhou | Updated: 2022-03-02 | Comments | Related: > Python

Problem

Web Crawling is a technique that can traverse web applications automatically and search for hyperlinks. The crawling method used by a web crawler varies from project to project. Since Web content is critical to successful online businesses, content strategists often need to gather, audit, and analyze existing content on their websites. To facilitate an in-depth understanding of their web content, they may want to use a computer program to crawl websites and capture introductory information, including page titles, internal links, external links, and keywords. How can IT professionals build a web crawler that helps content strategists to conduct a website content audit?

Solution

A website content audit is an accounting of the content that organizations currently have online (Halvorson & Rach, 2012). We can use technologies to conduct a quantitative audit thereby discovering objective facts about web content. The author's other article, "Using Advanced Python Web Scraping to Conduct a Web Content Audit," creates a web scraper to audit a single web page. When auditing multiple web pages or an entire website, we use web crawling techniques to crawl sites and capture basic information.

Note that the difference between "web scraping" and "web crawling" is relatively vague, as many authors and programmers use both terms interchangeably (Broucke & Baesens, 2018). However, they have different concerns. Loosely speaking, web scraping refers to data extraction from websites or web pages. The extracted data is often stored locally in a new file format, for example, on spreadsheets or database tables. On the other hand, web crawling explores web pages and discovers hyperlinks on these pages. Web crawling enables a computer program to navigate web pages on its own. When building a web crawler, we often apply either a depth-first search (DFS) algorithm or a breadth-first search (BFS) algorithm.

To create a scenario that we can relate to, we design a fictitious project to conduct a website content audit to demonstrate the web crawling techniques. MSSQLTips.com, owned by Edgewood Solutions, has served the SQL Server community since 2006. To understand what the website has, the CTO at Edgewood Solutions wants to audit administrative contents on the website. The administrative contents include all pages except articles, for example, the Copyright, Privacy, and Disclaimer pages. These administrative web pages are static pages whose content only depends on URLs.

This article first explains how a simple web crawler can traverse web pages on its own. Given an URL, the web crawler visits the web page and extracts URLs from the page. Then, the crawler accesses these new URLs to retrieve more URLs. The process repeats, and the crawler traverses the web to visit as many pages as possible. The repetition seems infinite; however, the project created in this article defines a scope for web crawling, i.e., the web crawler should visit administrative web pages only.

We also examine the website structure. A static web page usually contains URLs that link to other web pages. We model interconnectedness using the tools of graph theory. To scratch the surface of graph theory, we briefly review graph terminology and representations. We then explore the DFS and BFS algorithms. Next, the article provides Python programs to implement these algorithms and complete the project.

The author uses Microsoft Visual Studio 2019 to edit Python scripts and test these scripts using Python 3.9 (64-bit) programming language on Windows 10 Pro 10.0 <X64>. We draw graphs using the free online tool. To create an isolated environment for the project, the author adds a virtual environment to the project using this requirement.txt:

beautifulsoup4==4.10.0
boilerpy3==1.0.5
bs4==0.0.1
certifi==2021.10.8
charset-normalizer==2.0.11
idna==3.3
joblib==1.1.0
numpy==1.22.2
pip==20.2.3
requests==2.27.1
scikit-learn==1.0.2
scipy==1.8.0
setuptools==49.2.1
soupsieve==2.3.1
threadpoolctl==3.1.0
urllib3==1.26.8
xlwt==1.3.0

1 – Prerequisite

We use Python language to implement the DFS and BFS algorithms. To walk through this article, we should be familiar with the basics of Python language, Regular Expression, and the Beautiful Soup library. We should also know the steps to create a Python project and add a virtual environment using Microsoft Visual Studio. The following articles cover these topics:

Some familiarity with the recursive programming technique and the top-down design approach would be helpful. These two articles explore these two topics:

2 – The Web Graph

In computer science, the graph data structure consists of a finite set of vertices (or nodes) and a set of edges that connect these vertices. We can use a graph data structure to represent a set of objects that relate to each other. Since static web pages often contain hyperlinks that allow users to move seamlessly from one page to another, we can view web pages and these hyperlinks as a graph. Each web page is a vertex (or node), and each hyperlink, which takes users from one page to another, is a directed edge. We can apply the DFS or BFS algorithms to traverse the graph.

2.1 Graph Terminology

The graph data structure is one of the most widely used data structures with applications across computing, mathematics, and other related fields (Ejonavi, 2020). Because applications are so widespread and diverse, people have developed many terminologies to describe different elements and properties of graphs. Therefore, we should know some common terminologies when working with graphs.

2.1.1 Vertices, Edges and Graphs

Assuming a simple website contains five pages, A, B, C, D, and E. Figure 1 illustrates the relationships among these web pages. The vertices (or nodes), denoted by circles, represent web pages. The edges, denoted by segments that connect vertices, represent hyperlinks. The arrows on segments indicate the direction of the connection. After we name vertices, we can use a pair of vertices to denote an edge. For example, when there is a link to page B on page A, we use (A, B) to denote the edge. We refer to the set of all such vertices and directed edges as the web graph (Manning et al., 2008).

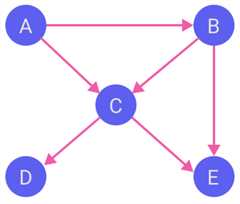
Figure 1 A Small Web Graph

In this simple web graph, the edges have a specific direction. For example, the edge (A, B) represents the connection from A to B. If all edges are unidirectional, we call the graph a directed graph or digraph. In that case, we refer to A as the source or parent vertex and B as the destination or child vertex (Guttag, 2016). However, Edges in a graph can be either directed or undirected (Ejonavi, 2020). The symbol {A, B} denotes an undirected edge between A and B. A graph with both directed and undirected edges is often called a mixed graph. We can convert an undirected or mixed graph into a directed graph. For example, we use two directed edges (A, B) and (B, A) to replace an undirected edge {A, B} (Goodrich & Tamassis, 2014).

We can use built-in data types or write Python classes to represent graphs and their components. For example, we use a python dictionary to represent a graph. In that case, a key in the dictionary maps an individual source node, and the key's corresponding value maps a list of destination nodes. This dictionary, called an adjacency list, consists of adjacent vertices for every vertex on the graph. For example, we use the following Python dictionary to represent the graph shown in Figure 1 (Klein, 2022):

edges = { 'A' : ['B','C'],
          'B' : ['C','E'],
          'C' : ['D','E'],
          'D' : [],
          'E' : []
        }

2.1.2 Graphs as a Python Class

We briefly discussed the four concepts: node, edge, digraph, and graph. Inspired by Professor Guttag, we write Python classes to represent these concepts. However, there is no straightforward and elegant way to represent a graph (Klein, 2022). This article provides a solution. We first define the node class. Then, since an edge has nodes, we use the composition technique to define the edge class. Next, we define the digraph class. Finally, we use the inheritance technique to define a subclass Graph, a specialized version of the parent class Digraph. The following code block presents the Python Node class. Section 4 gives the Internet address to download all other class definitions.

# Inspired by Professor Guttag's sample code (Guttag, 2016)
# The class represents a Node in a Graph.
class Node(object):
    '''
   Class that represents a Node
   '''
    # Overloading constructor. Called by Python each time a Node object is created.
    def __init__(self, name):
        '''
       Initializes instance variables (or instance attributes)
       '''
        # Assign the name to a Node
        self._name = name
 
    # Read the instance variable
    @property
    def name(self):
        '''
       Returns the name of a Node
       '''
        return self._name
    # Overloading __repr__, creates a canconical string represents an object
    def __repr__(self):
        '''
       Computes the "official" string representation of an object.
       This is the representation printed by the shell when evaluating the object.
       '''
        # Uses Python f-string to format output
        # Uses __name__ attribute of the class to get the class name
        return f"{type(self).__name__}({self._name})"
    # Overloading __str__, creates a pretty string representation of an object
    def __str__(self):
        '''
       Computes the pretty string representation of an object.
       This is the representation printed by the print() statement.
       '''
        return self._name

After defining classes to represent nodes, edges, digraphs, and graphs, we want to play a little bit with the simple web graph illustrated in Figure 1. So, we write a Python program to create a Digraph instance, shown in the following code block. The program demonstrates the use of the two methods defined in the Digraph class: has_node() and dests_of(). The has_node() method takes a node as the argument and determines if the node is in the digraph. The dests_of() method takes a node as the argument and returns a list of destination nodes.

from Digraph import Digraph
from Edge import Edge
from Node import Node
# Creates seven nodes
a, b, c, d, e = Node('A'), Node('B'), Node('C'), Node('D'), Node('E')
# Creates six unidirectional edges
ab, ac, bc = Edge(a, b), Edge(a, c), Edge(b, c)
be, cd, ce = Edge(b, e), Edge(c, d), Edge(c, e)
# Creates a Digraph
digraph = Digraph()
# Adds nodes to the Digraph
for node in [a, b, c, d, e]:
    digraph.add_node(node)
# Adds edges to the Digraph
for edge in [ab, ac, bc, be, cd, ce]:
    digraph.add_edge(edge)
# Print the string representation of the diagraph
print(digraph)
# Output:
#A->B
#A->C
#B->C
#B->E
#C->D
#C->E
# Tests the has_node() function
print(digraph.has_node(a))
# Output:
# True
# Tests the dests_of() function
print(digraph.dests_of(a))
# Output:
# [Node(B), Node(C)

2.1.3 Some Common Graph Terminologies

A graph is an abstract model of a network structure. Many applications, for example, social media networks, web pages, computer networks, and transportation networks, use these connectivity structures. In these applications, a fundamental operation is to traverse the graphs. Several graph algorithms are available to perform this operation (Mallawaarachchi, 2020). When applying graph theory in practice, we often come across these graph terminologies (Goodrich & Tamassis, 2014):

A vertex (or node) of a graph is an object that can connect to other objects.
An isolated vertex is a vertex that does not connect to any other vertices in the graph.
An edge is a connection between the vertices. An edge can be uni-directional or bi-directional.
A pair of parallel edges are two edges that have the same end vertices. For example, two uni-directional edges are parallel if they have the same source and destination.
A self-loop is an edge that connects a vertex to itself.
A weighted edge is an edge that associates a weight.
A graph is a data structure that consists of a finite set of vertices (or nodes) and edges connecting these vertices. Thus, a graph represents connections or relationships between pairs of objects.
An undirected graph is a graph in which all edges are bi-directional.
A directed graph, also called a digraph, is one whose edges are all directed.
A mixed graph is a graph that has both directed and undirected edges.
A weighted graph is a graph in which each edge associates a weight.
An unweighted graph is a graph in which each edge has no weights.
Adjacent vertices of a vertex are those vertices that connect to that vertex by edges.
An edge is an incident to a vertex if the vertex is one of the edge’s endpoints.
The order of a graph is the number of vertices in the graph.
The size of a graph is the number of edges in the graph.
The degree of a vertex is the number of edges incident to the vertex.
The outgoing edges (or out-degree) of a vertex are the directed edges whose source is that vertex.
The incoming edges (or in-degree) of a vertex are the directed edges whose destination is that vertex.
A path is a sequence of consecutive vertices. A simple path does not contain repeated vertices.
A cycle is a simple path where the last vertex is the same as the first.

Traversing the edges and vertices of a graph is a fundamental operation. We can examine all vertices and edges on the graph through a traversal. If the time spent on the traversal is proportional to the order and size of the graph, the traversal is efficient. We often use two traversal algorithms to visit nodes on a graph. They are depth-first search (DFS) and breadth-first search (BFS).

2.2 Depth-First Search Algorithm and Implementation

The depth-first search (DFS) algorithm traverses a graph using the backtracking technique to avoid getting stuck. When performing DFS, we begin at a specific starting node and then move to one destination of the start node. Then, the destination node becomes a new start node. We continue the process and move along a path. If we discover a dead end, we return to the previous node and look for an alternative path. If there is no alternative path, we continue to move backward one more node until we find an alternative path. The backtracking may lead us back to the start node. The process terminates when there are no more unvisited edges incidents on the start node.

2.2.1 Algorithm

When implementing DFS, we can use a stack data structure to support backtracking. We perform the insertion and deletion of an element only from one side of the stack. In that case, the stack follows the LIFO (Last In First Out) principle, i.e., the element inserted at last is the first element to come out. Additionally, we need to keep track of the visited nodes. The DFS algorithm works as follows:

Begin at a specific starting node, call it the current node, and add the current node to the visited node list.
Push all the current node's destination nodes into a stack.
The node at the top of the stack becomes the current node. Then, take the current node from the stack and add it to the visited node list.
Push all the current node's destination nodes not in the visited node list into the stack.
Repeat steps 3 and 4 until the stack is empty.

2.2.2 Explanation

We want to apply DFS to explore all nodes in the simple web graph, as shown in Figure 1. Table 1 illustrates the step-by-step process to implement the DFS.

Step	Traversal	Description
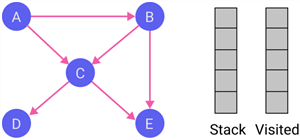
1		Initialize the stack and the visited list.
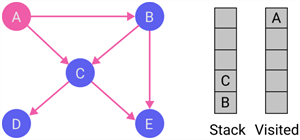
2		Begin from node A; therefore, node A is the current node. Then, put the current node to the visited list and push all its destination nodes, i.e., B and C, into the stack. Node C is at the top of the stack.
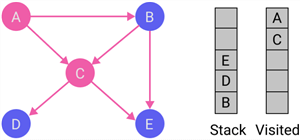
3		Node C becomes the current node. Put the current node C to the visited list and push all its destination nodes D and E into the stack. Node E is at the top of the stack.
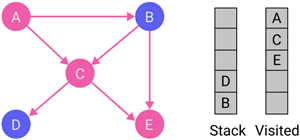
4		Node E becomes the current node. Put the current node E to the visited list, but Node E does not have destination nodes. So then, Node D is at the top of the stack.
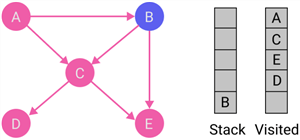
5		Node D becomes the current node. Put the current node D to the visited list, but node D does not have destination nodes. Therefore, node B is at the top of the stack.
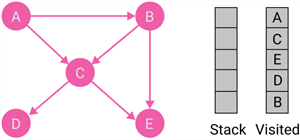
6		Node B becomes the current node. Put the current node B to the visited list. Node B has a destination node E, which is in the visited list already. The stack becomes empty; therefore, the process terminates.

Table 1 Depth-first Traversal Explained Step-by-Step

2.2.3 Implementation of DFS in Python

The DFS traversing process indicates that we can consider a node to be the start node when we reach the node. In other words, the problem of each node is a smaller version of the original problem. Therefore, the DFS algorithm has a recursive nature. Sometimes, recursion may provide clean and concise solutions for problems that may be difficult to solve with loops. In addition, recursion and looping share similarities: a recursive function can achieve any repetition task implemented by loops and vice versa (Zhou, 2020). This section provides an iterative and recursive implementation of DFS in Python.

2.2.3.1 Iterative implementation of DFS in Python

from collections import deque
from Digraph import Digraph
from Edge import Edge
from Node import Node
from Utility import find_all_unvisited_destination_nodes, print_path
# Uses stacks to implement the recursive nature of DFS.
def dfs_iterative(graph:Digraph, start:Node):
    '''
   Takes a digraph, starting node as arguments.
   Explores all nodes and prints the path.
   '''
    stack, visited, path = deque(), set(), list()
    # Picks a starting node and pushes it the stack.
    stack.appendleft(start)
    # Repeats the process until the stack is empty.
    while len(stack) > 0:
        # Pops a node from the stack and makes it current node.
        current_node = stack.popleft()
        # We do not want to visit the same node more than once.
        if current_node not in visited:
            # Marks the node as visited.
            visited.add(current_node)
            path.append(current_node)
            print_path(path)
            # Finds all unvisited destination nodes.
            unvisited_dest_nodes = find_all_unvisited_destination_nodes(graph, current_node, visited)
            if len(unvisited_dest_nodes) == 0:
                # Reaches dead end and backstepping occurs.
                while len(path) > 0 and len(
                    find_all_unvisited_destination_nodes(graph, path[-1], visited)) == 0:
                    path = path[:-1]
            else:                       
                # Pushes the unvisited destination nodes to stack.
                stack.extendleft(unvisited_dest_nodes)

Note that the above Python function invokes two user-defined functions: "find_all_unvisited_destination_nodes()" and "print_path()." Section 4 provides an Internet address to download the source code. In addition, the variables "path" and "visited" created inside the function are in the function's local scope. The number of elements in the "visited" list increases when the program traverses more nodes. When backstepping occurs, the program removes an element from the "path" list until finding an alternative path.

2.2.3.2 Recursive implementation of DFS in Python

from Edge import Edge
from Node import Node
from Digraph import Digraph
from collections import deque
from Utility import find_all_unvisited_destination_nodes, print_path
# Implement recursive depth-first search (DFS) algorithm
def dfs_recursive(graph:Digraph, current_node:Node, path:list = list(), visited = set()):
    '''
   Takes a digraph, current node as arguments.
   Constructs and prints the traversing path.
   '''
    # Marks the node as visited.
    # The function and the caller use the same list: visited.
    visited.add(current_node)
    # Created a new variable to store the path.
    new_path = path + [current_node]
    print_path(new_path)
    # Finds all unvisited destination nodes.
    unvisited_dest_nodes = find_all_unvisited_destination_nodes(graph, current_node, visited)
    if len(unvisited_dest_nodes) > 0:
        for node in reversed(unvisited_dest_nodes):                
            dfs_recursive(graph, node, new_path, visited)

The Python argument passing model is known as "Call by Object Reference" or "Call by assignment." If we pass immutable objects like whole numbers, strings, or tuples to a function, the passing is like call-by-value. The program cannot change the value of the immutable objects that we pass to the function. On the other hand, we can consider passing mutable objects to be call-by-reference (Klein, 2022). We use this feature to maintain the "visited" list. All recursive calls access the same list. However, to simulate the backstepping techniques, we create a new variable, "new_path," to store the traversing path. Therefore, recursive calls do not always access the same "path" object.

2.3 Breadth-First Search Algorithm and Implementation

Breadth-First Search (BFS) is another common approach to traverse a graph. We often use the iterative method to implement the BFS algorithm. In a breadth-first traversal, we begin at a starting node and then explore all destinations of the start node. We can consider the starting node to be at level 0 and its destination nodes to be at level 1. Next, we explore all destination nodes of every node at level 1. These new destination nodes are at level 2. The process expands level-wisely, and the program visits all destination nodes at the same level at a time. The process repeats until the program visit all nodes. Compared to the DFS algorithm, the BFS algorithm can effectively find the shortest path between two nodes (Hsu, 2021).

2.3.1 Algorithm

In DFS, we used a stack data structure to apply the LIFO principle. In that case, the program goes deeper and deeper in the graph till backtracking occurs. However, in BFS, we explore all nodes at the same depth level; therefore, we use a queue that follows the FIFO (First In First Out) principle. We also keep track of the visited nodes because we do not want to traverse a visited node. The BFS algorithm works as follows:

Begin at a specific starting node and place it into a queue.
Pop the front item of the queue and add the item to the visited node list.
Explore all destination nodes of the popped node and put all unvisited nodes at the back of the queue.
Repeat steps 2 and 3 until the queue is empty.

2.3.2 Explanation

We apply the BFS algorithm to explore all nodes in the simple web graph, as shown in Figure 1. Table 2 illustrates the step-by-step process to implement the BFS.

Step	Traversal	Description
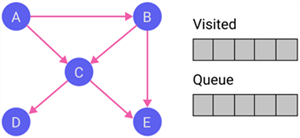
1		Initialize the queue and the visited list.
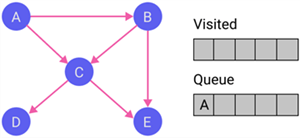
2		Begin from node A. Since the queue is empty, when we put the node at the back of the queue, the node sits at the front.
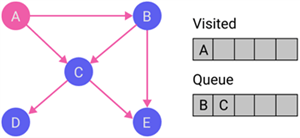
3		Discover all destination nodes of node A. Then, put all the unvisited destination nodes, i.e., B and C, at the back of the queue. Furthermore, put node A on the visited list.
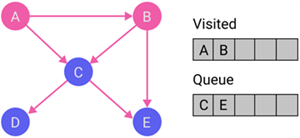
4		Discover all destination nodes of node B. Then, put the unvisited destination nodes, i.e., E, at the back of the queue. Moreover, we put node B on the visited list.
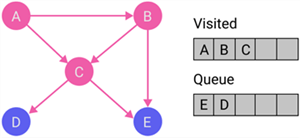
5		Discover all destination nodes of node C. Then, put the unvisited destination nodes, i.e., D, at the back of the queue. Furthermore, add node C to the visited list.
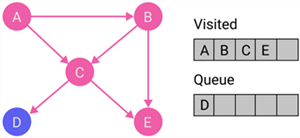
6		Discover all destination nodes of node E. The node does not have any destination node. Put node E to the visited list.
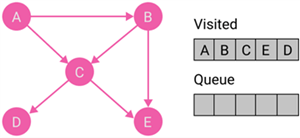
7		Discover all destination nodes of node D. The node does not have any destination node. Put node D to the visited list. The queue becomes empty; therefore, the process terminates.

Table 2 Bread-first Traversal Explained Step-by-Step

2.3.3 Implementation

from Edge import Edge
from Node import Node
from Digraph import Digraph
from queue import Queue
from Utility import find_all_unvisited_destination_nodes, print_path
# traverses level-wise from a starting node and uses a queue to store unvisisted nodes.
# Stores every path to the node into a list.
def BFS(graph:Digraph, start_node:Node):
    '''
   Takes a digraph, starting node as arguments.
   Explores all nodes and prints the path.
   '''
    queue, visited = Queue(), set()
    # Puts the starting node to the queue
    queue.put(start_node)
    # Initializes a path list that is a list of paths
    paths = [[start_node]]
    while queue.empty() == False:
        # Pops the item at the front of the queue.
        current_node = queue.get()   
        visited.add(start_node)        
        # Uses the list to implement FIFO rules.
        current_path = pathes.pop(0)
        print_path(current_path)
        # Finds all unvisited destination nodes.
        unvisited_dest_nodes = find_all_unvisited_destination_nodes(graph, current_node, visited)
        for dest_node in unvisited_dest_nodes:
            # Put the new destination node to the queue
            queue.put(dest_node)
            # Remembers the path to reach the destination node
            paths.append(current_path + [dest_node])

In the BFS implementation, we use a list to remember the paths from the starting node to specific nodes. If a node has an unvisited destination node in each iteration, we add the destination node to the path. We want to point out that the function marks a node as visited after the program dequeues the node from the queue. Alternatively, we can mark a node as visited when enqueuing a node into the queue.

3 – Creating a Web Crawler

To perform a website content audit, we first want to use a web crawler to discover the web pages. However, with the advent of new web technologies, web crawling can be more challenging. Many researchers and industrial groups provide solutions to address different issues and challenges (Mirtaheri et al., 2014). This article concentrates on solutions that can crawl traditional websites such as MSSQLTips.com. In a traditional website, we can access all the content through URLs.

3.1 Web Crawling

We can access all the content on a traditional website through URLs. First, a web crawler retrieves page contents for a URL. The web crawler then parses the downloaded contents and extracts other URLs. This process continues iteratively until the crawler explores all target web pages.

However, web technologies are evolving rapidly. As a result, new technologies always introduce challenges to web crawlers. For example, a web crawler can work with a traditional web application, but it may not work when crawling a Rich Internet Application (RIA). Therefore, we should select web crawling techniques accordingly. Table 3 summarizes three categories of web crawlers (Mirtaheri et al., 2014).

Category	Web Applications
Crawling Traditional Web Applications	Users can explore all the content of a web through URLs. We can use graph theory to help understand the structure of a web application and model the web application as a digraph. Nodes are pages with distinct URLs, and a directed edge represents a hyperlink on one page that points to another page.
Crawling Deep Web	A web application is database-driven. The web application generates web pages based on users' inputs. In that case, a web crawler may not access all web application contents merely by following URLs. However, we can still model the web application as a directed graph and consider pages to be nodes. A directed edge in the digraph represents a mechanism users can traverse from one page to another, such as submitting a form.
Crawling Rich Internet Applications	The web content does not depend on a URL in a web application because a web page can change content according to users' interactions. In this case, users change the state of DOM to retrieve different web content. Therefore, nodes represent the DOM states when we mode the web application as a digraph. A directed edge in the digraph represents a transmission between two DOM states.

Table 3 Different categories of web crawlers (Mirtaheri et al., 2014)

Today, many organizations, such as MSSQLTips.com, still use content management systems (CMS) to create and manage web content. Even though these websites are database-driven, all web content is reachable through URLs. Therefore, we can model these web applications as digraphs. We name these digraphs web graphs, as shown in Figure 1. Nodes are pages with distinct URLs, while a directed edge represents a hyperlink on one page that points to another page.

3.2 Traversing a Web Site

We discussed the DFS and BFS algorithms. These two algorithms provide solutions to traverse a web graph. A web crawler retrieves page contents for a URL, discovers new URLs on the page, and retrieves page contents for a new URL. The process repeats until the crawler explores all web pages in the scope. This process shows the nature of recursion; therefore, this article creates a web crawler that implements a recursive depth-first traversal algorithm.

3.2.1 Extracting Internal Links on a Web Page

The author’s other article (Zhou, 2021) provides a Python function "get_internal_links()" that can extract all URLs from a web page. We use that function in this article. We slightly modify the function and run a test. The following code block shows the source code of the function and the partial output of the program execution:

import re
import requests
from bs4 import BeautifulSoup
from urllib.parse import urljoin, urlparse
# Finds a list of all internal links
def get_internal_links(page_url:str, baseURL:str) -> set:
    '''
   Takes a beautiful soup object and base URL as arguments
   Returns a list of fully qualified internal links
   '''
    # Initializes the return value
    rtn_value = set()
    # Defines the regex to find internal links.
    regex = re.compile(r'^(' + baseURL + '\/|\/).+') 
    response = requests.get(page_url)
    soup = BeautifulSoup(response.content, 'html.parser')
    links = soup.find_all('a', {'href':regex})
    for link in links:
        try:
            href = link['href']
            # Removes the query string from the link
            url_path = urlparse(href).path
            # Gets fully qualified url
            fully_qualified_url = urljoin(base_url,url_path)
            rtn_value.add(fully_qualified_url)
        except AttributeError as e:
            pass
    return rtn_value
# The variable __name__ contains a string whose value depends on
# how the code is being used. A module's __name__ is set equal to
# __main__ when read from standard input, a script, or from an
# interactive prompt.
if __name__ == '__main__':  # Use this condition to determine the execution context.
    page_url = 'https://www.mssqltips.com/'
    base_url = 'https://www.mssqltips.com'
    urls = get_internal_links(page_url, base_url)
    print(*urls, sep='\n')
 
#Output
#https://www.mssqltips.com/sql-server-dba-resources/
#https://www.mssqltips.com/disclaimer/
#https://www.mssqltips.com/sqlserverauthor/57/rick-dobson/
#https://www.mssqltips.com/sqlservertip/1599/cursor-in-sql-server/
#https://www.mssqltips.com/sqlservertip/6429/sql-server-download-quick-links/
#https://www.mssqltips.com/sql-server-tutorials/
#...

3.2.2 A Simple Web Crawler

Since web crawling has a nature of recursion, we can use recursive techniques to write a clear and concise program that may be difficult to implement with loops. The following sample code provides a simple solution to crawl a website:

from collections import namedtuple
from Get_Internal_Links import get_internal_links
 
# To avoid an exhaustive site crawl, we add testing code to explore 10 pages
def traverse(page_url:str, base_url:str, visited:set, depth:int):
    '''
   Takes a page URL, a website base URL, a set and an integer as arguments
   Explores all internal link on the site
   '''
    # Adds this if statement to stop the recursion early
    if len(visited) > 10:
        exit()
    # The end of the testing code
    visited.add(page_url)
    # Discovers all unvisisted URLs on that page
    for link in get_internal_links(page_url, base_url):
        if link not in visited:
            print('Depth: {} URL: {}'.format(depth, link))
            # Invokes a recursive call
            traverse(link, base_url, visited, depth + 1)
# The variable __name__ contains a string whose value depends on
# how the code is being used. A module's __name__ is set equal to
# __main__ when read from standard input, a script, or from an
# interactive prompt.
if __name__ == '__main__':  # Use this condition to determine the execution context.
    page_url = 'https://www.mssqltips.com/'
    base_url = 'https://www.mssqltips.com'
    visited  = set()
    depth = 0
    traverse(page_url, base_url, visited, depth + 1)

Since every page contains links to other pages, the program may crash if it runs for a while. Furthermore, python limits the number of times a program can recursively call itself. By default, the recursion limit is 1000. Therefore, relying on recursion for web crawling is generally not a robust idea (Broucke & Baesens, 2018). However, our project asks us to explore all administrative contents on the MSSQLTips website. Therefore, this recursive technique should work for us. Moreover, as Mitchell mentioned, this recursive technique should be OK for any typical website we likely encounter (Mitchell, 2018).

4 – The Complete Source Code

The fictitious project asks us to audit administrative contents on the website MSSQLTips.com. We first need to create a web crawler to discover all administrative pages. This article has covered techniques to crawl a traditional website. We can apply the recursive depth-first algorithm to develop a web crawler. When retrieving web contents from a website, most robust crawlers separate the "crawling" part from the actual "scraping" part (Broucke & Baesens, 2018). After the web crawler extracts URLs, we pass these URLs to the web scraper to collect audit data.

By and large, the program that conducts the website content audit includes these steps:

Initializes variables, giving the landing page URL and the output folder.
Calls the recursive function to traverse web pages and save URLs into a Python set.
Loops through all URLs in the Python set.
Parses a page name from an URL.
Calls the web scrapping function to collect the audit data.

Click here for the complete code. After executing the program, the output folders should look like Figure 2.

Figure 2 The Excel Files Generated from the Website Content Audit

We present a simple version of the function "get_internal_links()" in Section 3.2.1. The function extracts all internal links on a web page. We make some changes to the regular expression to retrieve the administrative pages only. In practice, we should run some tests to ensure that the regular expression can capture all administrative pages. For demonstration purposes, we re-write the regular expression as follows:

regex = re.compile(r'^(' + base_url + '\/|\/)(?!(sql|search|mssqltips\-community)).+')

In addition, every web page on MSSQLTips.com contains a top menu section and a footer section. These two sections contain menus items. We remove these two sections from all pages except the landing page to avoid deep recursions. We can use the "PageElement.extract()" method to remove a tag from a beautiful soup tree. The following two Python user-defined functions show how to use the method:

# Removes the top bar section from the beautiful soup tree
def remove_top_bar_section(soup:object):
    '''
   Takes a beautiful soup object as an argument.
   Removes the top bar section from the beautiful soup tree
   '''
    top_section = soup.find("section", {'class':'top-bar-section'})
    top_section.extract()
 
# Removes the footer section from the beautiful soup tree
def remove_footer_section(soup:object):
    '''
   Takes a beautiful soup object as an argument.
   Removes the footer section from the beautiful soup tree
   '''
    soup.footer.extract()

Summary

We designed a fictitious project that provided a context to explore web crawling techniques. There are several categories of web crawlers. However, this article focuses on crawling traditional web applications. Mainly, the solution works for websites built on a content management system (CMS) platform.

We started with prerequisites on Python programming; we should be familiar with the basics of Python language, Regular Expression, and the Beautiful Soup library. At the same time, understanding the recursive programming techniques and the top-down design approach can help us walk through sample code.

We then covered some graph terminologies and used Python classes to define a graph and its components. After briefly introducing DFS and BFS algorithms, we explained the implementation of these algorithms by walking through examples step-by-step.

Next, we created a web crawler. After discussing the three categories of web crawlers, we provided simple solutions to traverse a website.

Finally, the article provided the complete source code that covers all steps to explore all administrative web pages on MSSQLTips.com, collect audit data and save data to Excel spreadsheets.

Reference

Bhadaniya, S. (2020). Depth First Search in Python (with Code) | DFS Algorithm. https://favtutor.com/blogs/depth-first-search-python.

Broucke, V. S. & Baesens, B. (2018). Practical Web Scraping for Data Science: Best Practices and Examples with Python. New York, NY: Apress.

Ejonavi, J. (2020). Data Structures 101: introducing graphs in JavaScript. https://www.educative.io/blog/data-structures-101-graphs-javascript.

Goodrich, T. M. & Tamassis, R. (2014). Algorithm design and applications. Danvers, MA: Wiley.

Guttag, V. J. (2016). Introduction to Computation and Programming Using Python. Cambridge, MA: The MIT Press.

Halvorson, K. & Rach, M. (2012). Content Strategy for the Web, Second Edition. Berkeley, CA: New Riders.

Hsu, R. (2021). Breadth First Search. https://medium.com/datascienceray/breadth-first-search-on-web-scarping-b25b0c7c21d.

Klein, B. (2022). Introduction to Applications of Python. https://python-course.eu/applications-python/

Mallawaarachchi, V. (2020). 10 Graph Algorithms Visually Explained. https://towardsdatascience.com/10-graph-algorithms-visually-explained-e57faa1336f3.

Manning, D. C., Raghavan, P., and Schütze, H. (2008) Introduction to Information Retrieval, Cambridge University Press.

Mirtaheri, M. S., Dinçktürk, E., M., Hooshmand, S., Bochmann, V. G., Jourdan, G. & Onut, V. I. (2014). A Brief History of Web Crawlers. https://arxiv.org/abs/1405.0749.

Mitchell, R. (2018). Web Scraping with Python, 2^nd Edition. Sebastopol, CA: O'Reilly Media.

Zhou, N. (2020). Recursive Programming Techniques using Python. https://www.mssqltips.com/sqlservertip/6549/recursion-in-python/.

Zhou, N. (2022). Using Advanced Python Web Scraping to Conduct a Web Content Audit. https://www.mssqltips.com/sqlservertip/7120/web-scraping-python-web-content-audit/.

Next Steps

To serve both organizations and users, we should conduct a content audit to analyze and assess web content systematically. Some organizations have interests in publishing as much content as possible to their website, or they do not remove aged content because they may think more content can provide more help. Nevertheless, more content may do more harm than good to the websites. For example, we may have experienced struggling to gather information from some websites. What is worse, some websites may provide contradictory information and confuse us. As a result, we may visit other websites and may never come back to these websites. In that case, web content failed to serve organizations and users. To use web content to achieve business objectives and meet users’ needs, these organizations should have a solid, centralized content strategy to guide content creation, delivery, and governance. A web content audit can help reveal strengths and weaknesses in the content strategy. This tip concentrates on a quantitative audit. There are some other content audits, and one of them is a qualitative audit. A qualitative audit conducted by human beings analyzes the quality and effectiveness of the web content based on defined characteristics (Halvorson & Rach, 2012).
Check out these related tips:

About the author

Nai Biao Zhou is a Senior Software Developer with 20+ years of experience in software development, specializing in Data Warehousing, Business Intelligence, Data Mining and solution architecture design.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips

Article Last Updated: 2022-03-02

Using Web Crawling in Python to Conduct a Website Content Audit