An Introduction to Assessing Normal Distribution with Python

By: Rick Dobson   |   Updated: 2023-02-01   |   Comments   |   Related: > Python

Problem

I seek a hands-on demonstration with Python to assess if a sample of values is normally distributed. I want a demonstration with both graphical and statistical approaches for assessing if a sample of data is normally distributed.

Solution

Assessing normality in a data sample is a classic task for statistics, data science, and data engineering practitioners. With a knowledge of the type of distribution for a dataset, you can judge whether data values are rare or common or compute the probability of a value falling within a confidence bound. Perhaps the most common distribution for many kinds of data is the normal distribution. Some other types of distributions commonly fitted to data samples have names like log normal, uniform, exponential, and binomial.

MSSQLTips.com has previously examined with T-SQL, how to fit different types of distributions to data samples (Using SQL to Assess Goodness of Fit to Normal and Uniform Distributions, Assessing with SQL and Data Science Goodness of Fit to Different Distributions and Using T-SQL to Assess Goodness of Fit to an Exponential Distribution). With the growing popularity of Python and data science, another approach is to use Python. As with many of my prior articles, the data samples are stock prices. So, if you are working with stocks, this can be an extra added benefit. However, no matter what data domain you are analyzing, this tip illustrates graphical and statistical techniques for assessing if values are normally distributed.

Pulling Data for This Tip

Historical prices for several securities tickers from a prior tip (Data Mining for Leveraged Versus Unleveraged ETFs) are provided to help you grow your skills at assessing with Python whether a dataset has a normally distributed column of values. Data for one ticker (SPY) are examined for 1994 and 2021 within this tip. You can use the sample scripts with other tickers and years to get more practice with the techniques covered in this tip.

Here's a T-SQL script to pull data for any of the datasets from the prior tip. The script relies on two local variables (@symbol and @year) to let users extract close values for a ticker symbol during a year. The script pulls SPY close values from 2021. Before displaying the close values, the script also displays some basic metrics for the sample, such as the mean and standard deviation of the sample values in the dataset.

-- declare variables
declare @year int, @symbol nvarchar(10)
 
-- process spy closes in 2021
select 
 @year = 2021
,@symbol = 'SPY';
 
drop table if exists #temp_closes;
 
-- populate #temp_closes for @symbol and @year
select [Close]
into #temp_closes
from [DataScience].[dbo].[symbol_date]
where symbol = @symbol  
and year(date) = @year
 
-- symbol, avg and sample standard deviation of close values
select 
 @symbol symbol
,@year [year]
,avg([Close]) avg_close
,stdev([Close]) stdev_close
from #temp_closes
 
-- display close values
select * from #temp_closes;

Here's an excerpt of the output from the preceding script:

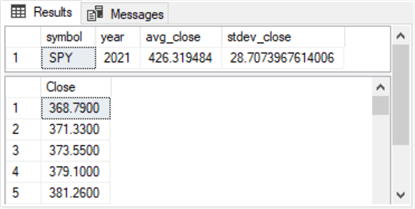
• The first pane identifies the sample dataset by ticker and year and provides two metrics for the sample. The two metrics (average and standard deviation) are often used to characterize a normally distributed set of values (what's the central value, and how are values dispersed on average about the central value).
• The second pane shows the first five close values in the dataset. In total, there are 252 SPY close values in the dataset for 2021. In general, there are about 252 trading days a year; each trading day's final trade indicates the close value for the day.

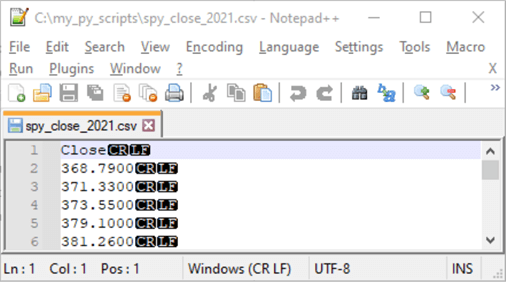
The list of close values and the column header are copied to a Notepad++ window. The data are saved with a CSV file format in the same path (c:\my_py_scripts\spy_close_2021.csv) as the Python scripts for assessing normality. The next section of this tip includes an illustration of one approach for reading a CSV file into Python.

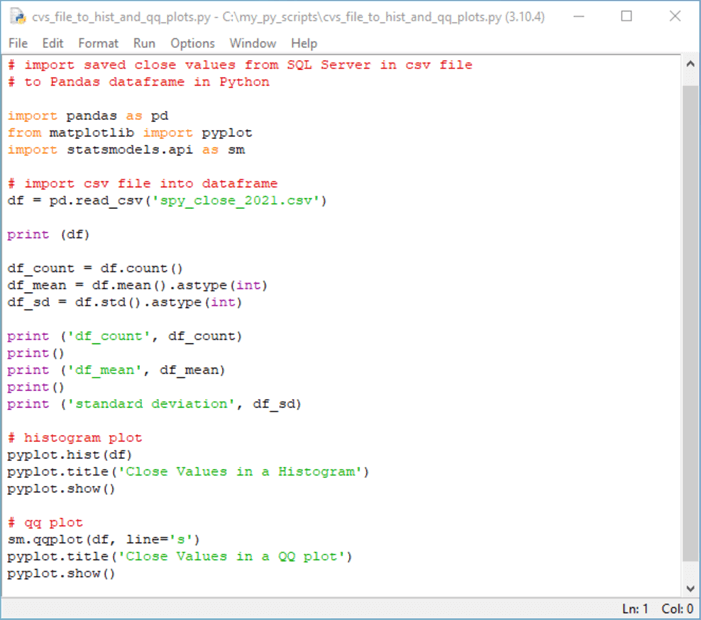
Importing, Processing, and Charting SPY Close Values from 2021

The script for this section shows how to create a histogram plot and a QQ plot for SPY close values in 2021. As you will see, these two plot types can help to visually assess if a dataset has normally distributed values.

• The script starts with three library references that the rest of the script needs to operate
  • The first library reference (import pandas as pd) imports the pandas library with an alias of pd; the library has a cvs_read function for reading a CSV file and returning a dataframe for use within Python
  • The second library reference (from matplotlib import pyplot) references the pyplot function library in the matplotlib application
    • pyplot has a built-in function for drawing a histogram based on column values from a dataframe or a Numpy array
    • the closer the bar chart is in appearance to a normal distribution, the more normal the underlying distribution
  • The third library reference (import statsmodels.api as sm) has a built-in function for computing and displaying qq charts. This type of chart displays sample quintile values to theoretical quintile values based on a normal distribution. The closer the sample quintile values are to the theoretical quintile values, the more normal the sample values are. The term quintile is used to denote the cumulative percent of values in a dataset below a designated value
  • If you do not have any of the libraries referenced in code samples throughout this tip installed on your computer, you can use the Python Install Program (pip) to install them. An internet search will provide numerous examples of how to use pip to install any of the libraries. For example, here is a link to a web page for installing the pandas library with two sets of instructions. The second answer was ranked as most helpful by the person posing the question
• The first line of code after the library references invokes the read_csv function to import the spy_close_2021.csv file and returns a dataframe named df
• Then, a print function displays by default the first and last five rows in the df dataframe
• Next, the count, mean, and standard deviation of values are saved and printed
• The next three lines create and display a histogram based on the values in df
• The last three lines create a qq plot of the sample quintile values versus the theoretical quintile values based on a normal distribution. For those who would like a brief introduction to qq plots, you can try either of these online resources (here and here)

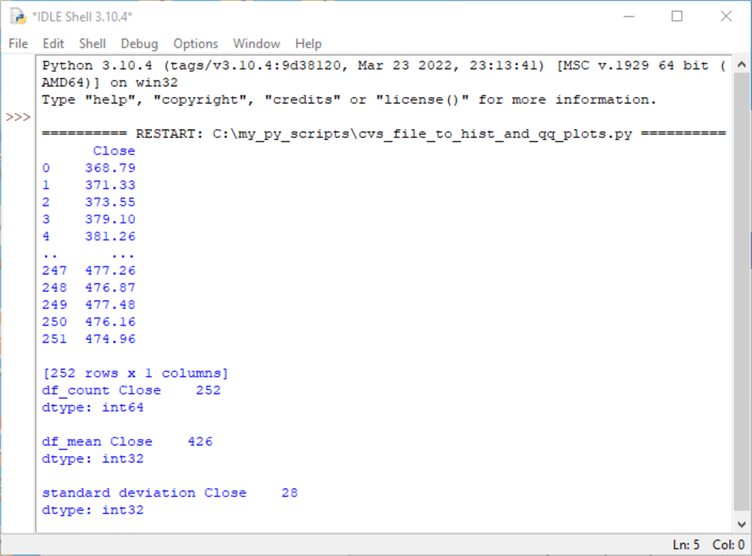
Here is the IDLE Shell window populated by the preceding script. The IDLE application is a development environment that downloads when you install Python from the Python.org website.

• The first and last five rows in the dataframe appear first
  • The first column of printed values is for the dataframe index row values
    • 0 through 4 are for the first five rows
    • 247 through 251 are for the last five rows
  • The second column values are for the actual values in the dataframe from the source CSV file. Notice that the second column values match the first five rows in the CSV file from the Notepad++ image at the end of the preceding section
  • After the first and last five rows, the IDLE Shell window displays the dimension for the df dataframe – namely, a single column with 252 rows
• The next three pairs of rows show the integer values for the count of dataframe rows as well as the mean and standard deviation of close values

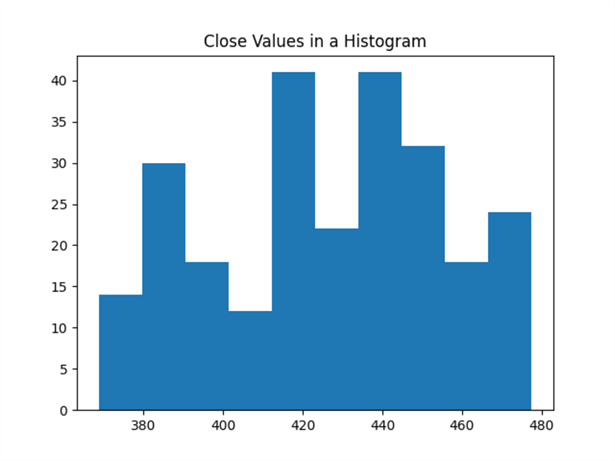
After displaying the shell window, the script presents two images. The first image is a histogram of the close values in the df dataframe. Notice that the histogram bars do not resemble a bell-shaped normal curve. This is because the left and right tails of the chart do not decline much relative to the central tendency of the chart bars. Also, there is a bar at the center of the x-axis that is dramatically shorter in height than the bars to either side of it. A histogram for a normally distributed set of values peaks at its central value, which is the mean, the median, and the mode for a normal distribution of values.

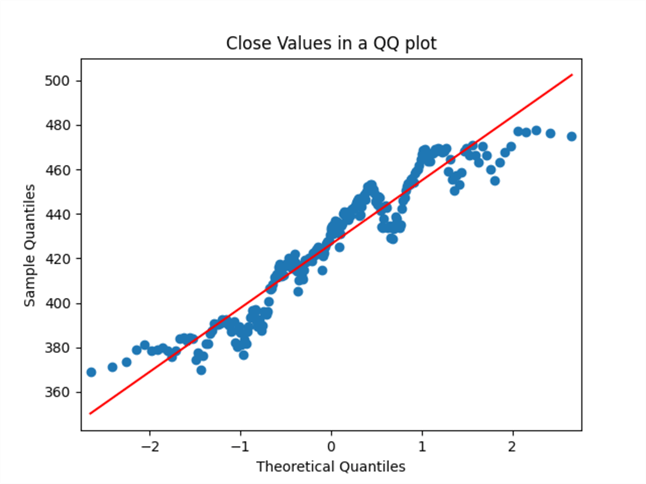
The next chart is the qq chart. It plots sample quintile values versus theoretical quintile values based on a normal distribution. If the values fall along the red diagonal line, then the data are normally distributed. As the plot of sample quintile values versus theoretical quintile values diverges from the diagonal line, the goodness of fit of the sample distribution to a normal bell-shaped curve diminishes.

Displaying Histogram and QQ Plots for Random Normally Distributed Values

The two plots in the preceding section do not offer strong visual support for the values in the df dataframe being normally distributed. However, could the weak support merely reflect random variations in sample values? One way of answering this question is to compute 252 gaussian random univariate values with a mean of 426 and a standard deviation of 28. Recall that the df dataframe in the prior section had 252 values with a mean of 426 and a standard deviation of 28.

The Numpy library for Python contains a pseudo-random univariate number generator for standard normal deviation values. The generated values approximate values drawn from a standard normal distribution with a mean of 0 and a standard deviation of 1. These standard normal deviate values can be transformed into a set of general normal deviate values by multiplying the standard deviate values by a scale factor based on the standard deviation of the general normal distribution and then adding a mean value to the transformed values for the central value of the general normal distribution.

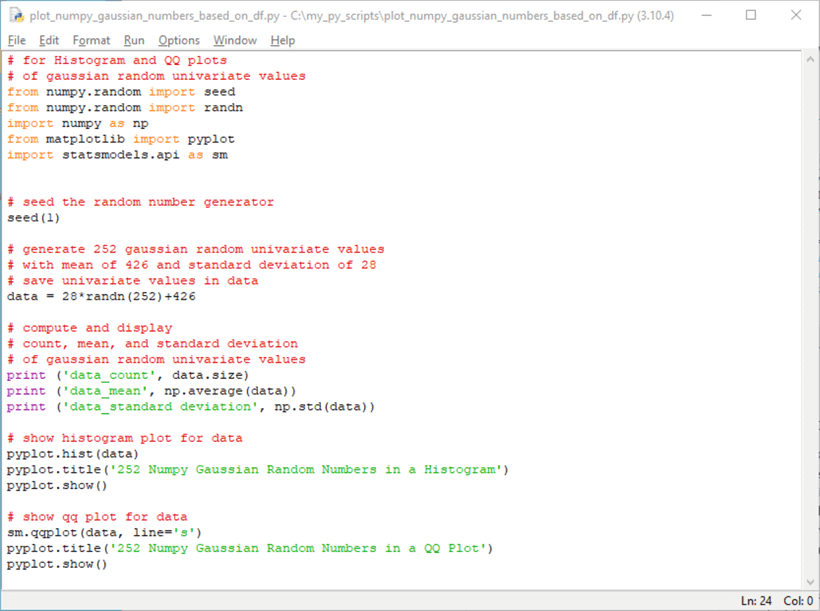
Using the general normal deviate values as input to Python code for displaying histogram and qq plots, we can see what random general normal deviate values plots should look like. The following Python script shows how to accomplish this. The histogram and qq plots from the script in this section can be compared to the histogram and qq plots in the preceding section to see how the sample values from the preceding section compare to values that are known to be drawn from a general normal distribution of 252 values with a mean of 426 and a standard deviation of 28.

• The library references include three lines of code not in the script from the prior section
  • The first reference is for the Numpy seed function. This function lets you designate a value for generating the same random sequence based on the argument for the seed function
  • The second reference is for the Numpy randn function. The randn function returns univariate normally distributed values
  • The third reference is for the general Numpy library. This library enables the computation of the count, mean, and standard deviation for values from a transformed distribution based on values returned by the randn function
  • The last two library reference statements are discussed in the prior section's script. These two libraries enable the generation of histogram and qq plots based on a distribution of values from a dataset or a Numpy array
• The statement after the library references gives an example of how to assign a value to the seed function
• The next statement shows how to specify the generation of 252 random values with the randn function; this statement also shows an expression for transforming the standard random deviate values with a mean of 0 and standard deviation of 1 to a mean of 426 and a standard deviation of 28 in a general normal distribution
• The next three statements show how to compute the count, mean, and standard deviation of the values in the general normal distribution; these are values in a Numpy array named data
• The next to the last three statements and the last three statements, respectively, generate histogram and qq plots for the values in the general normal distribution values (data)

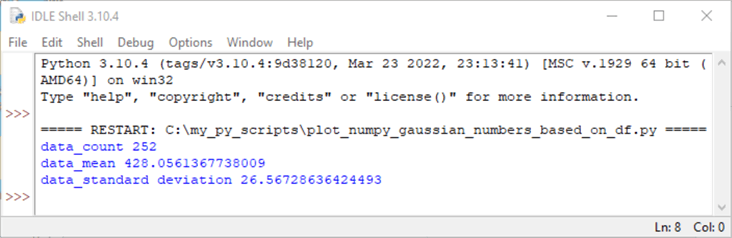
The following screenshot shows the count, mean, and standard deviation of the values in the data array. Notice that the mean value is 428.06. This does not perfectly match the transformation applied to the underlying univariate random values from the randn function. The deviation is explained by the random values returned by the randn function. Using a different seed value would result in a slightly different mean value.

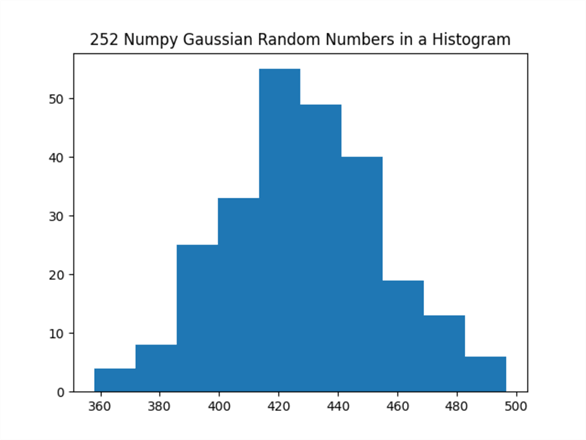
Here is the histogram plot generated by the preceding script file.

• The histogram has a peak histogram bar containing a data value of 426, which is the central value of the sample distribution examined in the preceding section
• The tails for the histogram chart decline as the bars move away from the central value

Here is the qq plot generated by the preceding script.

• Nearly all the points in the qq plot fall directly on the diagonal red line, and those that do not fall directly on the red line fall very near to it
• This indicates that sample quantile values from the Numpy array closely match the theoretical quantile values for a normally distributed set of values

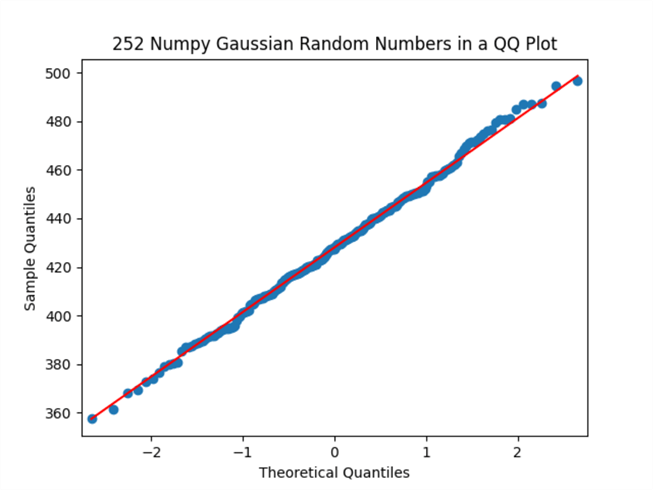
Across both the histogram and qq plots in this section, there is strong support that the values in the data array are normally distributed. This is not surprising because the data values were derived from a pseudo-random number generator for standard normal values. In contrast, the histogram and qq plots from the preceding section based on sample observations for SPY close values in 2021 do not strongly support the hypothesis that the sample close values are normally distributed. Because the sample SPY close values have the same mean and standard deviation as the normally distributed values from the Numpy randn function, but their histogram and qq plots appear substantially different, it is easy to conclude that the sample SPY close values are not normally distributed based on visual inspection.

Assessing Whether Values are Normally Distributed Based on a Statistical Test

There are multiple statistical tests for assessing whether the values in a test are normally distributed. Each test evaluates a different aspect of what it means for values to be normally distributed. A popular and powerful test is known as the Shapiro-Wilk test for normality. This test computes a statistic and reports the probability of rejecting the null hypothesis: the tested data are normally distributed. If the probability value for the computed statistic:

• Is less than or equal to .05, then you can reject the null hypothesis (that the underlying data are normally distributed).
• Is not less than or equal to .05, then you cannot reject the null hypothesis; this means the Shapiro-Wilk test cannot reject the assumption of a normally distributed dataset.

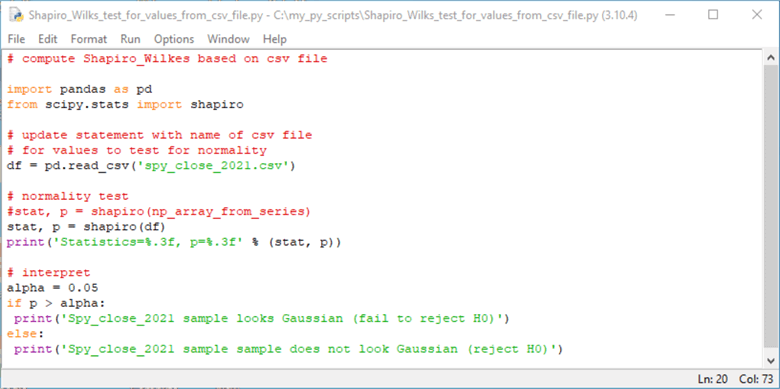
The Shapiro-Wilk test can be implemented with the Shapiro function from within the scipy.stats library for Python. The following two screenshots show two different use cases for the Shapiro function.

• The first use case assesses if the values in the CSV file are normally distributed. The use case references a CSV file with close values for the SPY ticker in 2021. After the library references, there are three steps to the use case
  • The first step is to read the CSV file into a dataframe (df)
  • The second step is to implement the normality test and display the results. The results consist of the computed statistic value (stat) and its probability of occurrence
  • The third step is to reject or not reject the null hypothesis of no difference between the values in the source dataframe and a normally distributed set of values
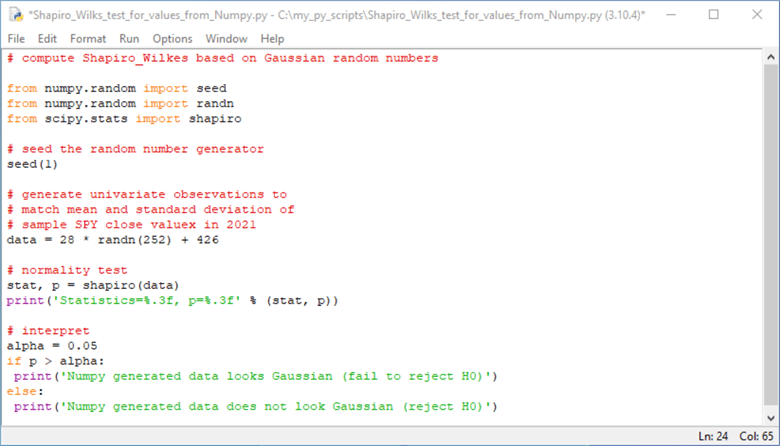
• The second use case assesses if it is possible to reject the assumption of normality for values from a Numpy array populated by a gaussian pseudo-random number generator. After the library references, there are four steps to the use case
  • Designate a seed value for the returned values from the randn function
  • Run the randn function and transform the standard normal distribution values to a general normal distribution of values
  • Implement the normality test and display the results. The results consist of the computed statistic value and its probability of occurrence
  • Reject or do not reject the null hypothesis of no difference between the transformed values from the Numpy randn function and distribution of normal values

The next screenshot shows sequentially the results from the first and second use cases.

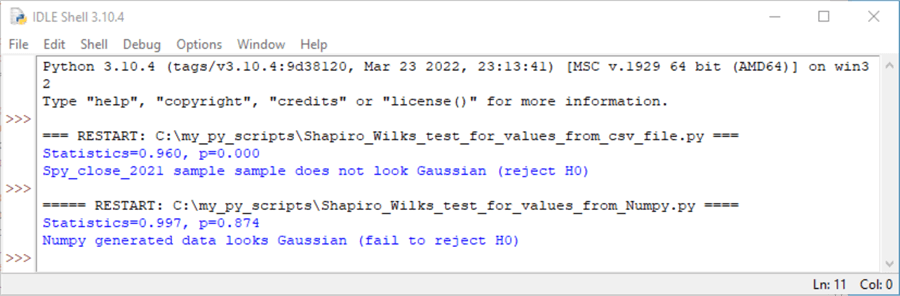
• The first use case results assess if the assumption of normality can be rejected for the values in the CSV file. Because the p-value is less than .05, the assumption of normality can be rejected. The values in the CSV file are not normally distributed.
• The second use case results assess if the assumption of normality can be rejected for the transformed values returned from the randn Numpy function. Because the p-value is not less than or equal to .05, then the assumption of normality cannot be rejected. The values in the data Numpy array look Gaussian.

Normality Charts and Statistical Tests for SPY Close Values from 1994

To help demonstrate key points in the tip to this point, the code for the histogram and qq plots, as well as the code for the statistical test for normality (Shapiro_Wilk), is presented for SPY close values from 1994. Here is the code for 1994 SPY close values. This script is identical to the example in the "Importing, processing, and charting SPY close values in 2021" section, except for the parameter for the read_csv method.

• In the prior section, the file name parameter is spy_close_2021.csv.
• In this section, the file name argument is spy_close_1994.csv.
• Therefore, the data in this section is from 1994 as opposed to 2021 in the prior section.

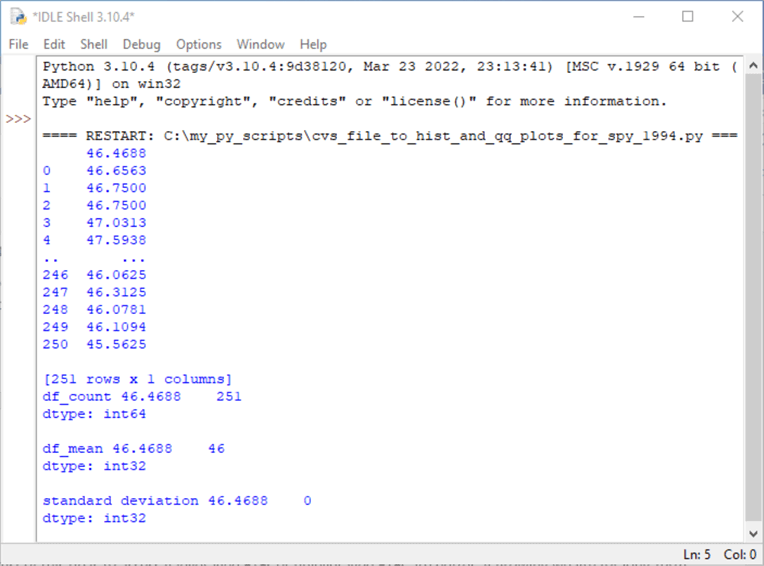
The next screenshot shows the contents of the IDLE Shell window after running the preceding script. The contents of this window are different from the same window based on data from 2021.

• The close values are smaller on average in 1994 than in 2021. This is because 1994 close values are nearer to the initial SPY public offering in 1993 than to close prices from about 28 years after the initial public SPY offering.
• Also, the number of close values is less by one in 1994 than in 2021. The number of trading days in a year can change slightly depending on the number of weekend days in a year, the day of the week for some market holidays, or even because of severely adverse weather conditions that shut down the operation of the market on what would have been a regular trading day.

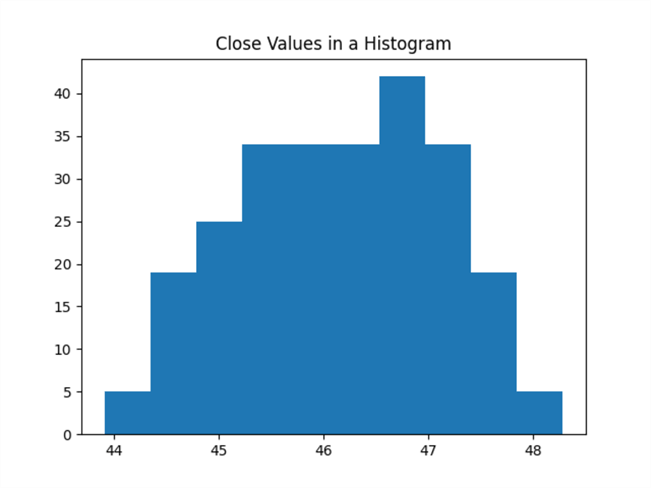
Here's the histogram plot of close values from 1994.

• Notice that the close value with the largest frequency is displaced towards the right side of the distribution.
• Also, there is a skew towards the smaller close values.

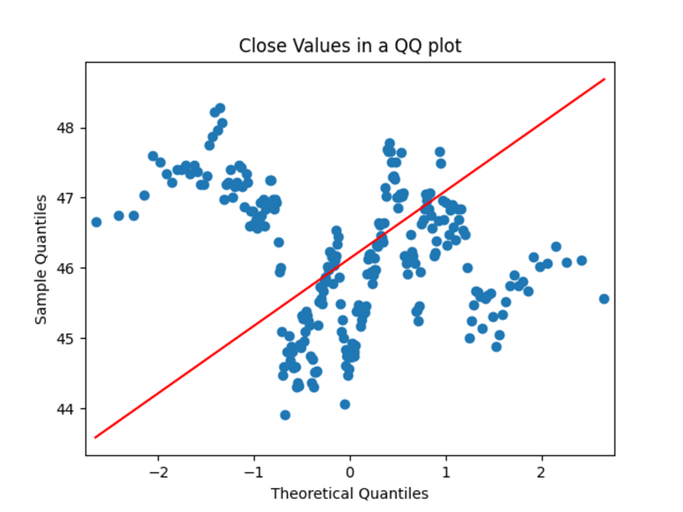
The next screenshot shows a qq plot of the sample quintiles versus the theoretical normal quintiles. The qq plot highlights that the 1994 SPY close values are not normally distributed. This is because the points in the plot do not generally fall on or near the red diagonal line.

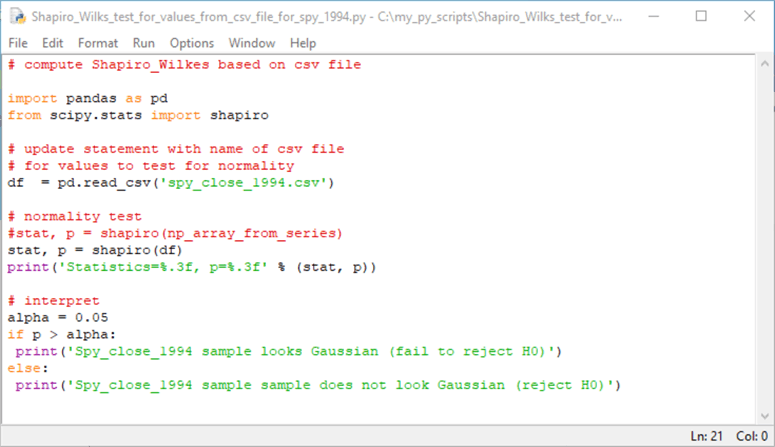
Here is the script for computing the Shapiro-Wilk test for normality with 1994 SPY close values. This script is like the one for 2021 SPY close values, except for the file name argument for the read_csv method.

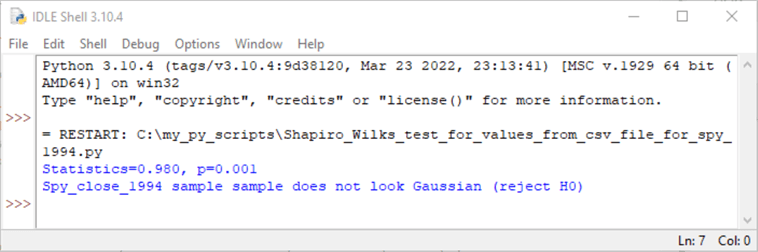
Here's the IDLE window after running the script. As you can see, the script results show a rejection of normally distributed values. This outcome is consistent with the distribution of points in the qq plot for SPY close values from 1994.

Next Steps

The main thrust of the tip is to show the steps with Python for assessing the normality of a set of values from a dataset. This tip presents multiple Python examples and explains the code for all the Python scripts. The tip also shows and describes the significance of the results from running the code for a sample of close values for the SPY ticker in 2021. To illustrate how to apply the Python normal distribution assessment techniques for close values in another year, the main assessment techniques are additionally presented for close values from 1994.

This tip's download includes the source data files with SPY close values for the results presented throughout this tip. This will allow you to verify that you can run the code after installing Python and the required libraries. This tip's download also includes files with close values for selected other tickers for multiple years. This fresh data was not processed in the tip; the fresh data will give you a chance to start from scratch with another sample besides that used in the tip.

Here is a list of the files in the download for this tip.

• There is a SQL script file named "close values for symbol and year.sql" for pulling close values by ticker symbol and year from the symbol_date table
• A CSV file named "ticker symbols with open high low close and volume values.csv" for populating the symbol_date table; this CSV file contains historical price and volume data for the SPY ticker as well as other tickers across multiple years
• Two additional CSV files (spy_close_2021.csv and spy_close_1994.csv) with close values that are extracted from the symbol_date table and configured for the examples in this tip; see the "Pulling data for this tip" section for a summary of this process
• There are six Python script files referenced in the tip. These files demonstrate the techniques for assessing if a dataset contains normally distributed values. Here are the Python file names
  • cvs_file_to_hist_and_qq_plots.py
  • plot_numpy_gaussian_numbers_based_on_df.py
  • Shapiro_Wilk_test_for_values_from_csv_file.py
  • Shapiro_Wilk_test_for_values_from_Numpy.py
  • cvs_file_to_hist_and_qq_plots_for_spy_1994.py
  • Shapiro_Wilk_test_for_values_from_csv_file_for_spy_1994.py

About the author

Rick Dobson is an author and an individual trader. He is also a SQL Server professional with decades of T-SQL experience that includes authoring books, running a national seminar practice, working for businesses on finance and healthcare development projects, and serving as a regular contributor to MSSQLTips.com. He has been growing his Python skills for more than the past half decade -- especially for data visualization and ETL tasks with JSON and CSV files. His most recent professional passions include financial time series data and analyses, AI models, and statistics. He believes the proper application of these skills can help traders and investors to make more profitable decisions.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips