Performing a Wilcoxon Signed Rank Test in SQL Server

By: Rick Dobson   |   Updated: 2021-05-26   |   Comments   |   Related: > TSQL

Problem

I have heard that data scientists sometime use the Wilcoxon signed rank test to assess if paired measurements on a set of entities, such as persons, cars, or stocks, are significantly different from one another. Please demonstrate how to implement the Wilcoxon signed rank test with T-SQL. Also, include multiple datasets that help me understand when to use the Wilcoxon signed rank test versus another statistical test for assessing if paired measurements on a set of entities are significantly different from one another.

Solution

The Wilcoxon signed rank test is one of two widely recommended statistical tests for assessing if two repeated measurements on a sample of entities are statistically different. The t-test for paired comparison measurements is the other widely recommended statistical test for assessing if two repeated measurements on a sample are statistically different. The primary difference between the two tests is that the t-test assumes the differences are from a population of normally distributed differences. On the other hand, the Wilcoxon signed rank test does not require that the differences be from a population of normally distributed differences.

The sign test is another statistical test for assessing if two sets of measurements for a sample of paired comparisons are statistically different. The sign test examines if the sign of the differences are consistently positive or negative at a statistically significant level. Unlike the t-test for paired comparison measurements and the Wilcoxon signed rank test, the sign test does not consider the magnitude of the differences for each pair in a sample.

This tip drills down on the how to compute the Wilcoxon signed rank test with three different examples.

• The first example gives the T-SQL code for computing a signed rank test statistic. The code in this tip automates the manual instructions for computing the test statistic as described in an internet published textbook on statistics. This example allows the verification of the T-SQL code relative to a known outcome. By this tip achieving the same outcome from the T-SQL code as the book reports, you can be assured of the validity of the code for use with other examples. It is generally a good practice to confirm T-SQL code for relatively complex statistical operations with a standard reference before using it with fresh data.
• The second example was originally presented in a demonstration of how to run a t-test for a sample of paired comparisons measurements. By running the signed rank test for the data from this example, you can gain a feel for the power of both tests at assessing the statistical significance of the differences between the measurements.
• The third example data was originally used to demonstrate how to run a sign test for a set of twelve pairs where each pair contrasted the performance of a particular stock symbol relative to a symbol based on the S&P 500 index, which is a common benchmark for overall stock performance. This example provides yet another use case for applying the Wilcoxon signed rank test and provides more insight about which test to use to the difference between paired comparison measurements.

Overview of the Wilcoxon signed rank test

This tip highlights four constraints for data used in a Wilcoxon signed rank test.

1. Two measurements are performed for each sample entity from a single population, such as students at a school or stock symbols traded in a stock exchange.
2. The measurements must be for a continuous variable even if they are only reported to the nearest integer.
3. The difference of measurements for each pair must at least have the properties of an ordinal scale so that it is meaningful to speak of differences in the measurements for each pair as greater than, equal to, or less than each other.
4. The difference of the measurements for each pair must not equal 0. If a pair of measurements has a zero difference between its measurements, then it is removed from the sample before computing the statistical significance of the signed rank test. This is because a difference of 0 contributes no information about whether the first measurement or the second measurement is greater. Also, the difference between two measurements on a continuous scale cannot be 0.

The reason the test is called the signed rank test is because ranks convey ordinal scale information even for differences based on continuous variables. A rank of 2 is one rank value greater than a rank of 1, and a rank of 3 is one rank greater than a rank of 2. A dataset for three paired comparisons can have continuous variable differences 2, 4, and 8 with ranks of 1, 2, and 3. Each successive continuous variable difference is twice as large as the preceding difference, but difference in ranked values is always just one from the first, to the second, to the third ranked value.

According to the central limit theorem in statistics, the sum of a random variable, such as a set of ranks, is normally distributed as the number of sums increase. The Wilcoxon signed rank test applies rank values to paired comparison differences. Based on the central limit theorem, the sum of the signed ranks can be interpreted as a value in a normal distribution.

In this tip, the focus is on whether the first measurement is greater than or less than the second measurement in a paired comparison.

• In an upper tailed directional test, z, the normal deviate, is greater than 0. An upper tailed test outcome is for when the first measurement is larger than the second measurement in the paired comparison. Statistically significant critical z values are as follows
  • 1.282 for a .10 significance level
  • 1.645 for a .05 significance level
  • 1.960 for a .025 significance level
  • 2.326 for a .010 significance level
  • 2.576 for a .005 significance level
  • 3.090 for a .001 significance level
• In a lower tailed directional test, z is less than 0, and the critical z values are less than 0. A lower tailed test outcome is for when the second measure is larger than the first measurement. Statistically significant critical z values are as follows
  • -1.282 for a .10 significance level
  • -1.645 for a .05 significance level
  • -1.960 for a .025 significance level
  • -2.326 for a .010 significance level
  • -2.576 for a .005 significance level
  • -3.090 for a .001 significance level
• These critical z values are derived from professor Wayne W. LaMorte’s post on the Boston School of Public Health website.

The Verification Example for Wilcoxon signed rank T-SQL code

The following T-SQL script displays the data for the Wilcoxon signed rank verification example. This example is called the verification example because the outcome from the T-SQL code is compared to a known outcome for a common set of source data. The T-SQL code below is readying data for a Wilcoxon signed rank test described in the Concepts and Applications of Inferential Statistics textbook published on the internet.

• The code begins by creating a fresh copy of data_for_Wilcoxon_test table in the DataScience database. The table has three columns
  • The first column (comp_id) is populated with a string identifier value for each paired comparison
  • The second column (apply1_result) is the first measurement for a paired comparison
  • The third column (apply2_result) is the second measurement for a paired comparison
• The insert into statement after the create table statement populates the data_for_Wilcoxon_test table with the data for the verification example.
• The first select statement after the insert into statement displays all 16 rows of sample data.
• The delete statement after the first select statement removes two rows with equal values for first and second measurements. Recall that rows with a zero difference do not contribute any information about the statistical significance of the difference between the first and second measurements from a dataset of paired comparison measurements.
• The second select statement after the delete statement displays the 14 rows for which the Wilcoxon signed rank test is performed.

use DataScience
go
 
-- create and populate a fresh copy of data_for_Wilcoxon_test table
drop table if exists data_for_Wilcoxon_test
 
create table data_for_Wilcoxon_test
(
comp_id varchar(10) not null,
apply1_result real not null,
apply2_result real not null
)
 
-- data from Concepts & Applications of Inferential Statistics by Richard Lowry
-- Subchapter 12a: http://vassarstats.net/textbook/ch12a.html
-- demonstrating the computation of the Wilcoxon Signed Rank Test
 
insert into data_for_Wilcoxon_test
values
   ('comp_1', 78, 78),
   ('comp_2', 24, 24),
   ('comp_3', 64, 62),
   ('comp_4', 45, 48),
   ('comp_5', 64, 68),
   ('comp_6', 52, 56),
   ('comp_7', 30, 25),
   ('comp_8', 50, 44),
   ('comp_9', 64, 56),
   ('comp_10', 50, 40),
   ('comp_11', 78, 68),
   ('comp_12', 22, 36),
   ('comp_13', 84, 68),
   ('comp_14', 40, 20),
   ('comp_15', 90, 58),
   ('comp_16', 72, 32)
 
-- display rows in data_for_Wilcoxon_test
-- before removing ties
select * from data_for_Wilcoxon_test
 
-- remove ties
delete 
from data_for_Wilcoxon_test
where apply1_result = apply2_result
 
-- display rows in data_for_Wilcoxon_test
-- after removing ties
select * from data_for_Wilcoxon_test

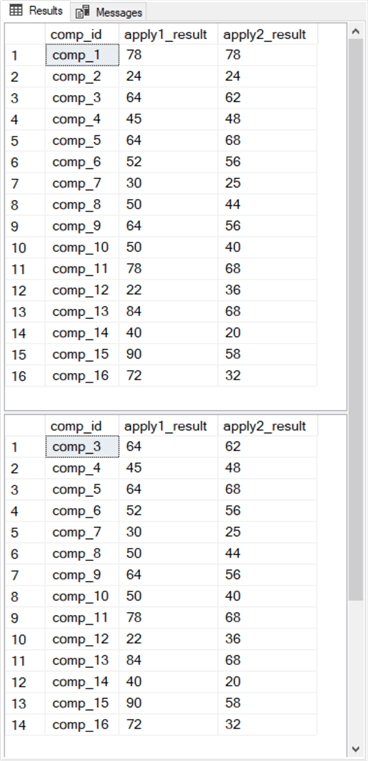
Here is the output from the preceding script.

• The first window within the Results tab is the results set from the first select statement with 16 rows.
• The second window within the tab is the results set from the second select statement with 14 rows.
• The Wilcoxon signed rank test is performed for the dataset in the second window.

The next step for computing a Wilcoxon signed rank test requires the computation of the absolute differences for each set of paired comparison measurements as well the computation of a column of signed rank column values. Here is the code for the differences for pairs of measurements in the data_for_Wilcoxon_test table.

select 
 comp_id
,apply1_result
,apply2_result
,(apply1_result - apply2_result) [difference]
,sign(apply1_result - apply2_result) sign_for_difference
,abs(apply1_result - apply2_result) abs_difference
from data_for_Wilcoxon_test

The differences for pairs of measurements are processed in several ways.

• The difference column returns the difference of the first measurement less the second measurement.
• The sign_for_difference column returns a value of 1 when the first measurement for pair is greater than the second measurement and a value of -1 otherwise.
  • The SQL Server sign function facilitates this objective.  While the SQL Server sign function can return a value of 0 when there is no difference between its two arguments, the preprocessing for the data_for_Wilcoxon_test table removes all rows from the original source data with equal values for apply1_result and apply2_result.
  • Later, the sign_for_difference column values will be used to assign signs to rank values for the differences between pairs of measurements for a row.
• The abs_difference column returns the absolute value of the difference for measurements for each row.

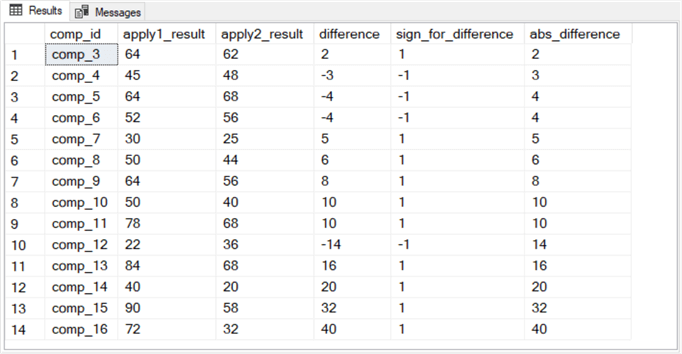
Here is what the results set from the preceding script looks like for the first Wilcoxon signed rank test example.

• Notice there are 14 rows in the results set.
• Two pairs of rows (3 and 4 as well as 8 and 9) have matching absolute difference values. For these two pairs of rows, the Wilcoxon test requires an average rank value – namely, 3.5 for rows 3 and 4 as well as 8.5 for rows 8 and 9.

T-SQL comes with a set of built-in ranking functions. Unfortunately, none of these built-in functions generates rank values exactly like what the Wilcoxon signed rank test requires when the absolute differences for two or more consecutive rows are the same. Here is a T-SQL script excerpt for computing the signed rank values based on the requirements of the Wilcoxon signed rank test.

-- join unsigned and signed ranks with matching abs_difference values
-- to differences from data_for_Wilcoxon_test
 
select 
 Wilcoxon_differences.*
,unsigned_rank.unsigned_rank
,(Wilcoxon_differences.sign_for_difference * unsigned_rank) signed_rank
from
(
-- add difference, sign, abs difference, 
-- to data for Wilcoxon test
select 
 comp_id
,apply1_result
,apply2_result
,(apply1_result - apply2_result) [difference]
,sign(apply1_result - apply2_result) sign_for_difference
,abs(apply1_result - apply2_result) abs_difference
from data_for_Wilcoxon_test
) Wilcoxon_differences
 
join
 
(
-- compute avg row_number (unsigned_rank) for abs_difference values
select abs_difference, avg(rownumber) unsigned_rank
from
(
-- list rownumber by abs_difference
select 
 abs_difference
,rownumber
from
(
-- extract abs_difference from data_for_Wilcoxon_test
-- and compute matching row_number
select 
 abs(apply1_result - apply2_result) abs_difference
,cast(row_number() over(order by abs(apply1_result - apply2_result)) as float) rownumber
from data_for_Wilcoxon_test
) for_avg_rownumber
group by abs_difference, rownumber
) for_avg_rownumber
group by abs_difference
) unsigned_rank
 
on Wilcoxon_differences.abs_difference = unsigned_rank.abs_difference

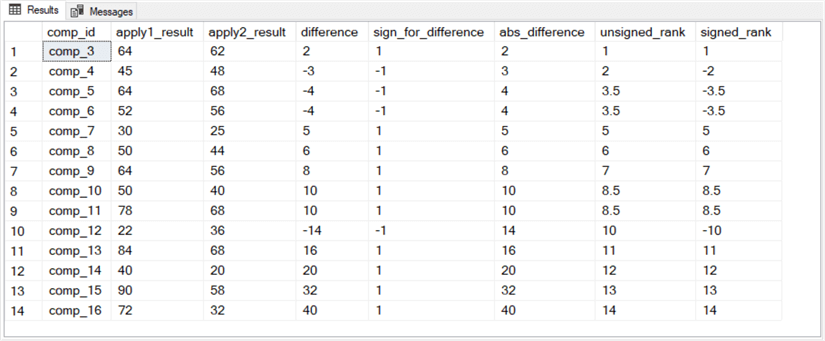
The easiest way to understand the code in the preceding script window may be to examine its results set, which appears in the next screen shot. Notice that rows are sorted according to their abs_difference value. The signed_rank column values depend on the unsigned_rank column values. The signed_rank column values for each row are computed as the product of the unsigned _rank column values times the sign_for_difference column values.

The unsigned column rank values depend on the average of row_number () function values ordered and grouped by abs_difference column values. Rows with the same absolute difference values have an identical rank value; these identical values can be fractional values, such as 3.5 for the third and fourth rows and 8.5 for the eighth and ninth rows. The rank value for the unsigned_rank column is based on the average row_number () function value for rows with the same abs_difference values. If you are already familiar with the row_number () function you probably recall that it returns an integer value. Therefore, to compute an untruncated average rank value for two or more rows with the same abs_difference value, the code casts the return value from the row_number () function as a float value. Then, the avg function computes the average untruncated rank across rows with the same abs_difference value.

For sample sizes of 10 or more rows, the sum of the signed_rank values is approximately normally distributed. The maximum positive sum of signed ranks for the approximately normal distribution is

(N(N+1))/2, where N is the number of signed ranks

For a sample size of 14 as in this example, the maximum possible sum of unsigned rank values is 105 when all rank values are positive. Conversely, the minimum sum of signed ranks where all rank values are negative is -105 when all rank values are negative. Therefore, the sum of the possible signed rank values begins with a minimum value of -105 and extends through a maximum value of +105.

• The greater the number of negative signed ranks, the closer the sum of the unsigned rank is to -105.
• The greater the number of positive signed ranks, the closer the sum of the unsigned ranks is to +105.

Professor Lowry’s book states that the standard deviation for the population of the sum of the signed ranks is

sqrt((N(N+1)(2N+1))/6) 

For the sample size of 14 rows in the preceding table, the standard deviation rounded to two places after the decimal is 31.86.

The expression for the normal deviate value (generally denoted as z) when W represents the sum of the signed rank values is one of two values

(W - .5)/ sqrt((N(N+1)(2N+1))/6) when W is greater than 0

or

(W + .5)/ sqrt((N(N+1)(2N+1))/6) when W is less than 0

Finally, in this example where the sum of the signed rank values is 67 in the sample data source, the z value can be approximated by

(67 - .5)/31.86 or 2.09

The computed z value from the preceding expression can be compared to the critical z values for different significance levels from the "Overview of the Wilcoxon signed rank test" section to assess if the W value is statistically significant, and if so at what level. For the selection of rows in the preceding table, the computed z value is significant at the .025 level in an upper tailed directional test.

The T-SQL code for computing the W, N, standard deviation, and z value is as follows.

-- @n is for the number of signed ranks
-- @sum is for sum of signed ranks
declare @n int, @sum int
 
select 
   @n = count(signed_rank)
 ,@sum = sum(signed_rank)
 
from
(
-- join unsigned ranks with matching abs_difference values
-- to differences from data_for_Wilcoxon_test
 
select 
 Wilcoxon_differences.*
,unsigned_rank.unsigned_rank
,(Wilcoxon_differences.sign_for_difference * unsigned_rank) signed_rank
from
(
-- add difference, sign, abs difference, 
-- to data for Wilcoxon test
select 
 comp_id
,apply1_result
,apply2_result
,(apply1_result - apply2_result) [difference]
,sign(apply1_result - apply2_result) sign_for_difference
,abs(apply1_result - apply2_result) abs_difference
from data_for_Wilcoxon_test
) Wilcoxon_differences
 
join
 
(
-- compute avg row_number (unsigned_rank) for abs_difference values
select abs_difference, avg(rownumber) unsigned_rank
from
(
-- list rownumber by abs_difference
select 
 abs_difference
,rownumber
from
(
-- extract abs_difference from data_for_Wilcoxon_test
-- and compute matching row_number
-- cast row_number() as float to be able to compute average row_number () within abs_difference
select 
 abs(apply1_result - apply2_result) abs_difference
,cast(row_number() over(order by abs(apply1_result - apply2_result)) as float) rownumber
from data_for_Wilcoxon_test
) for_avg_rownumber
group by abs_difference, rownumber
) for_avg_rownumber
group by abs_difference
) unsigned_rank
 
on Wilcoxon_differences.abs_difference = unsigned_rank.abs_difference
)for_@n_and_@sum
 
-- compute z for sum of signed ranks
select 
 @sum W
,@n N
,sqrt((@n*(@n+1)*(2*@n+1))/6) [standard deviation of signed ranks]
,case
   when @sum > 0 then
      (@sum - .5)/sqrt((@n*(@n+1)*(2*@n+1))/6)
   else(@sum + .5)/sqrt((@n*(@n+1)*(2*@n+1))/6)
 end [z for sum of signed ranks]

Here is the results set from the preceding script excerpt. You can confirm the code by comparing the results set values to the expression results for the Wilcoxon signed rank test in Professor Lowry’s textbook.

Wilcoxon signed rank test versus a paired comparison t-test

The Wilcoxon signed rank test is commonly referred to by data scientist practitioners as a non- parametric statistical test. This test is analogous to the paired comparison t-test, which is a parametric test. Both tests work with a dataset of paired comparison measurements.  A prior MSSQLTips.com article drills down on t-tests in general and features a section illustrating how to program a paired comparison t-test and assess its statistical significance level with T-SQL. This section of the current tip applies the Wilcoxon signed rank test script verified in the preceding section to the same dataset as in the prior tip. The statistical significance reported by both tests should help you understand one key difference between the tests and why it is so important.

The following Results tab is from the T-SQL code for the paired comparison t-test described in the prior article. The bottom window in the Results tab shows the paired comparison data. The data show two sets of miles per gallon measurements from ten cars. The first data column (apply_1_result) is for miles per gallon for a tank full of premium gasoline. The second data column (apply_2_result) is for miles per gallon for a tank full of regular gasoline. Assume a researcher used

• a null hypothesis that premium gasoline did not result in greater miles per gallon across the ten cars, and
• an alternative hypothesis that premium gasoline did result in greater miles per gallon across the ten cars

A statistically significant result allows a data science practitioner to reject the null hypothesis and accept the alternative hypothesis. This kind of hypothesis calls for a one-tailed directional test. The top window in the following screen shot shows the outcome of the paired comparison t-test for the data. As you can see, the significance level is beyond the .001 level. In other words, there is no more than one chance in a thousand that a computed t value could be as great as 4.472… if the premium gasoline did not deliver better gas mileage in the population from which the measurements were drawn.

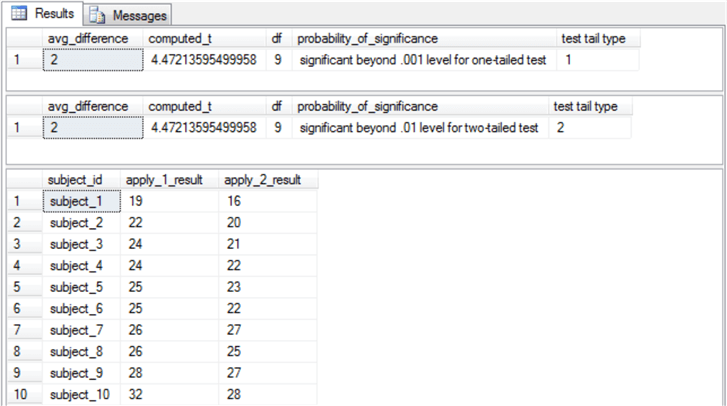
The next screen shot shows the same data being processed to compute the Wilcoxon signed rank test. In the preceding screen shot, the cars are identified by subject_id values of subject_1 through subject_10. In the following screen shot, the same cars are identified by comp_id values from comp_1 through comp_10. The rows in the following screen shot are sorted by abs_difference values while the rows in the preceding screen shot are ordered by subject_id value.

Recall that the Wilcoxon signed rank test assigns signed_rank values to the paired comparison measurements based on the abs_difference and sign_for_difference column values. When the abs_difference value is the same for two or more rows, then the unsigned rank will be identical. However, the underlying measurement values can be different for rows with same unsigned_rank value.

• For example, comp_7, comp_8, and comp_9 each have abs_difference values of 1. These three cars share the same unsigned_rank value of 2.
• You can see that the miles per gallon measurements for comp_9 (28 and 27) are higher than those for comp_8 (26 and 25). Nevertheless, both rows have the same unsigned_rank value of 2.
• Similar divergences between the miles per gallon measurements and the unsigned_rank values exist for some of the other cars. 
  • For example, the cars with comp_id values of comp_2 and comp_5 both have an unsigned_rank value of 5, but the apply1_result and apply2_result measurements are substantially: 22 and 20 for comp_2 versus 25 and 23 for comp_5.
  • Similarly, cars with identifiers of comp_6 and comp_1 both share unsigned_rank values of 8, but the apply1_result and the apply2_result values are larger for comp_6 (25 and 22) than for comp_1 (19 and 16).
• Clearly, the t-test paired comparison statistic works with data that are more granular (appl1_result and apply2_result) than the Wilcoxon signed rank test (signed_rank). All other things equal, this can lead to finer resolution of differences for the t-test than for the Wilcoxon signed rank test.

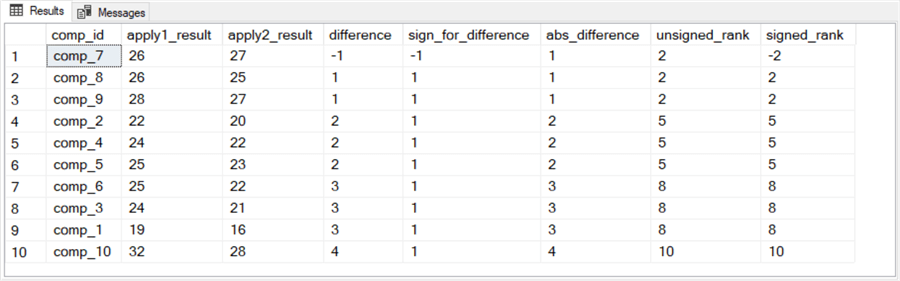
Here is the T-SQL results set with the statistical significance indicator (computed z value) for the cars with identifiers comp_1 through comp_10. The computed z value for the signed ranks is 2.57…, which is 51 divided by 19.621… The computed z value indicates a statistically significant difference from the Wilcoxon signed rank test of .01 based on the critical z values in the "Overview of the Wilcoxon signed rank test" section. However, the t-test reported the differences as significant as beyond the .001 level. For this set of data, the significance level is ten times greater for the t-test than for the Wilcoxon signed rank test.

The t-test achieves its greater resolution of differences relative to the Wilcoxon signed rank test with more rigid assumptions about the population of the source data as well as the degree of resolution for determining differences from paired comparison measurements.

• The t-test is a parametric test that assumes a set of paired comparison differences are normally distributed. The normal distribution has a shape. Therefore, if your paired comparison differences have positive or negative outlier values, then the t-test is not appropriate for determining the significance level of the differences between paired comparison measurements.
• The Wilcoxon signed rank test does not work with the differences between paired comparison measurements on an interval scale. Instead, it works with differences based on an ordinal scale. When the data are drawn from a survey of consumer preferences (such as 1 star, 2 stars, through 5 stars), then differences between paired comparisons are not likely to be on an interval scale. Instead, you can only use an ordinal scale to assess the difference between replies. When the paired comparison measurements are assessed on an ordinal scale, then the t-test is not appropriate for determining the significance level of the differences between paired comparison measurements.

Wilcoxon signed rank test versus a sign test

A prior MSSQLTips.com article, Performing a Sign Test with T-SQL, demonstrates how to program a sign test for two different datasets. Unlike the Wilcoxon signed rank test, the sign test does not compare the magnitude of the differences between paired comparison measurements. Instead, the sign test just searches for how many times one member of a paired set of measurements exceeds the other member of a paired set of measurements.

The sign test is based on a coin toss analogue. If you toss a coin 12 times, it grows increasingly unlikely that you will obtain 9, 10, 11, or even 12 heads out of 12 tosses. Similarly, it is exceedingly unlikely that the second measurement for paired comparison measurements will be larger than the first member of a pair for 9, 10, 11, or 12 times out of 12 comparisons. The prior article on how to program a sign test with T-SQL gives you the details on how to program the sign test and determine the statistical significance of the test for up through 20 paired comparisons.

The two different datasets for this section compare the percentage gain of each of two stock symbols (SOXL and PYPL) to another stock symbol (SPY) that returns a benchmark metric – namely, the percentage gain of the S&P 500 index. The sign test for the two datasets allows you to see which, if either, of the comparison stock symbols exceeds the S&P 500 index across 12 monthly periods.

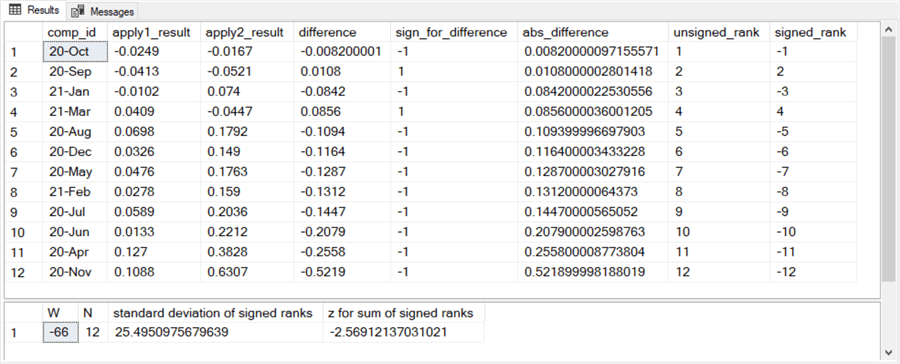
Here are the Wilcoxon signed rank test results for the SOXL symbol (apply2_result) vs the SPY symbol (apply1_result). A careful examination of the top window in the following screen shot shows that the SOXL symbol had a larger percentage gain in 10 out of 12 months. The z value (-2.569…) in the bottom window is statistically significant at beyond the .01 level -- that is, there is less than 1 chance in 100 of obtaining this z value if the apply2_result values (percentage gains for the SOXL symbol) do not systematically exceed the apply1_result values (percentage gains for the SPY symbol).

The prior tip reported the significance level for the sign test as 0.016. Because the statistical significance of the difference is greater the lower the significance level, the Wilcoxon signed rank test gave a slightly better outcome than the sign test for this dataset from the prior article.

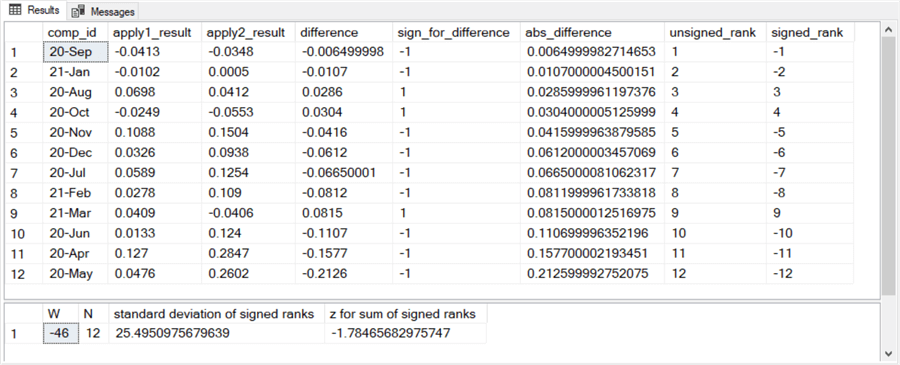
Here are the Wilcoxon signed rank test results for the PYPL symbol (apply2_result) versus the SPY symbol (apply1_result). For these paired comparisons, PYPL percentage gains (apply2_result) exceeded SPY percentage gains (apply1_result) for 9 out of 12 months. In addition, the computed z variate from the T-SQL script for the signed rank test was -1.784, which is statistically significant at beyond the .05 level.

The prior tip that compared PYPL percentage gains to SPY percentage gains based on the sign test was only able to confirm a statistically significant difference at the .10 significance level, which is twice as high as significance level detected by the Wilcoxon signed rank test.

In summary, the Wilcoxon signed rank test was marginally to substantially more effective than the sign test at discovering a difference between the paired comparison measurements in both datasets. One reason for this, may be because the sign test ignores the magnitude of the difference between paired measurements, but the Wilcoxon signed rank test factors in the sign as well as the rank of the magnitude of the difference between paired measurements. If you are only interested in how many times one member of pair of measurements exceeds another, then the sign test may be an acceptable choice. However, if you are concerned with size of the differences as well as the number of times one measurement exceeds another, then the Wilcoxon signed rank test may be your best choice.

Next Steps

If you want to add the Wilcoxon signed rank test to the repertoire of tools you use in your data science projects, I encourage you to re-run the T-SQL code for computing the Wilcoxon signed rank test for any of the four datasets referenced in this tip.

This tip’s download filecontains a single script with four commented blocks that can generate all the results displayed in this tip.

• The script is designed to use a database named DataScience. Either create a database named DataScience on your SQL Server instance or change the use statement at the top of the script to reference another database of your choice.
• Each commented block includes an insert into statement followed by a delete statement sandwiched between two select statements. Each commented block is for one of the four datasets referenced in this tip.
• To re-create the results any one of the four datasets referenced in this tip, simply edit out the comment markers for the corresponding block of code inserting the data into the data_for_Wilcoxon_test table.

You can also insert your own block of code to add a fresh dataset for which to compute the Wilcoxon signed rank test.

About the author

Rick Dobson is an author and an individual trader. He is also a SQL Server professional with decades of T-SQL experience that includes authoring books, running a national seminar practice, working for businesses on finance and healthcare development projects, and serving as a regular contributor to MSSQLTips.com. He has been growing his Python skills for more than the past half decade -- especially for data visualization and ETL tasks with JSON and CSV files. His most recent professional passions include financial time series data and analyses, AI models, and statistics. He believes the proper application of these skills can help traders and investors to make more profitable decisions.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips